第九章统计章末检测题(含答案)
文档属性
| 名称 | 第九章统计章末检测题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 901.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-19 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第九章统计章末检测试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷解答题又分必考题和选考题两部分,选考题为二选一.考生作答时,将所有答案写在答题卡上,在本试卷上答题无效.本试卷满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.
2.选择题答案使用2AB铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,书写要工整、笔迹清楚,将答案书写在答题卡规定的位置上.
3.所有题目必须在答题卡上作答,在试卷上答题无效.
第Ⅰ卷 (选择题共60分)
一.选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.学校组织班级安全知识竞赛,某班的12名学生的成绩(单位:分)分别是:58,67,73,75,76,82,82,
87,90,92,93,98,则这12名学生成绩的第一四分位数是( )
72分 B. 73分 C. 74分 D.75分
2.已知某工厂生产A,B,C三种不同型号的产品,某月生产A,B,C这三种型号的产品的数量之比为1:a:2,现用分层抽样的方法抽取一个容量为60的样本,已知B型号产品被抽出30件,则a的值为( )
A. 4 B. 3 C. 2 D. 1
3.已知数据x1,x2,…,x30的极差为6,方差为2,则数据2x1+1,2x2+1,…,2x30+1的极差和方差分别为( )
A. 18,2 B. 12,4 C. 6,8 D. 6,4
4.在简单随机抽样中,某一个个体被抽到的概率( )
A.与第几次抽样有关,第一次被抽到的概率最大 B.与第几次抽样有关,第一次被抽到的概率最小
C.与第几次抽样无关,每一次被抽到的概率相等 D.与第几次抽样无关,与抽取几个样本有关
5.根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精含量在
80 mg/100 mL以上(含80)时,属醉酒驾车.某地对涉嫌酒
后驾车的28800人进行血液检测,根据检测结果绘制的频
率分布直方图如图.则这28800人中属于醉酒驾车的人数
约为( )
A.8 640 B.5 760
C.4 320 D.2 880
6.北京冬奥会已于2022年2月4日至2月20日顺利举行,这是中国继北京奥运会,南京青奥会后,第三次举办的奥运赛事.之前,为助力冬奥,提高群众奥运法律知识水平和文明素质,某市有关部门开展冬奥法律知识普及线上答题,共计30道题,每道题2分,满分60分.现从参与线上答题的市民中随机抽取1000名,将他们的作答成绩分成6组,并绘制了如图所示的频率分布直方图.若同一组中的数据用
该组区间中点值为代表,可估计这次线上答题成
绩的平均数为( )
33 B. 34
C. 35 D. 36
7.某班有50名学生,在一次考试中统计出平均分数为
70,方差为75,后来发现有2名学生的成绩统计有误,学
生甲实际得分是80分却误记为60分,学生乙实际得分是70分却误记为90分,更正后的平均分数和方差分别是( )
A.70和67 B.70和50 C.75和50 D.75和67
8.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.两组工人完成生产任务的工作时间(单位:min)为:
第一种生产方式:68,72,76,77,79,82,83,83,84,85,86,87,87,88,89,90,
90,91,91,92
第二种生产方式:65,65,66,68,69,70,71,72,72,73,74,75,76,76,78,81,
84,84,85,90
则下列结论中,表述不正确的是( )
A.第一种生产方式的工人中,有75%的工人完成生产任务所需要的时间至少80 min
B.第二种生产方式比第一种生产方式的效率更高
C.这40名工人完成任务所需时间的中位数为80 min
D.无论哪种生产方式的工人完成生产任务平均所需要的时间都是80 min
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分.
9.关于简单随机抽样,下列说法正确的是( )
A.它要求被抽取样本的总体的个数有限 B.它是从总体中逐个地进行抽取
C.它是一种不放回抽样 D.它是一种等可能性抽样
10.某校高一800名学生参加了数学检测,
将所有学生的数学成绩分组如下:[90,100),
[100,110),[110,120),[120,130),[130,140),
[140,150],得到的频率分布直方图如图所示,
下列说法中正确的是( )
A.成绩不低于120分的学生人数为1220.
B.这800名学生中数学成绩的众数为125.
C.若本次测试合格率定为60%,则至少得118分才能合格.
D.这800名学生数学成绩的平均数为12
11. 已知数据x1,x2,…,xn的平均数为,标准差为s2,则( )
A.数据x12,x22,…,xn2的平均数为,标准差为s2
B.数据2x1,2x2,…,2xn的平均数为2,标准差为2s
C.数据,x1+2,x2+2,…,xn+2的平均数为+2,标准差为s2
D.数据2x1-2,2x2-2,…2xn-2的平均数为2-2,标准差为2s2
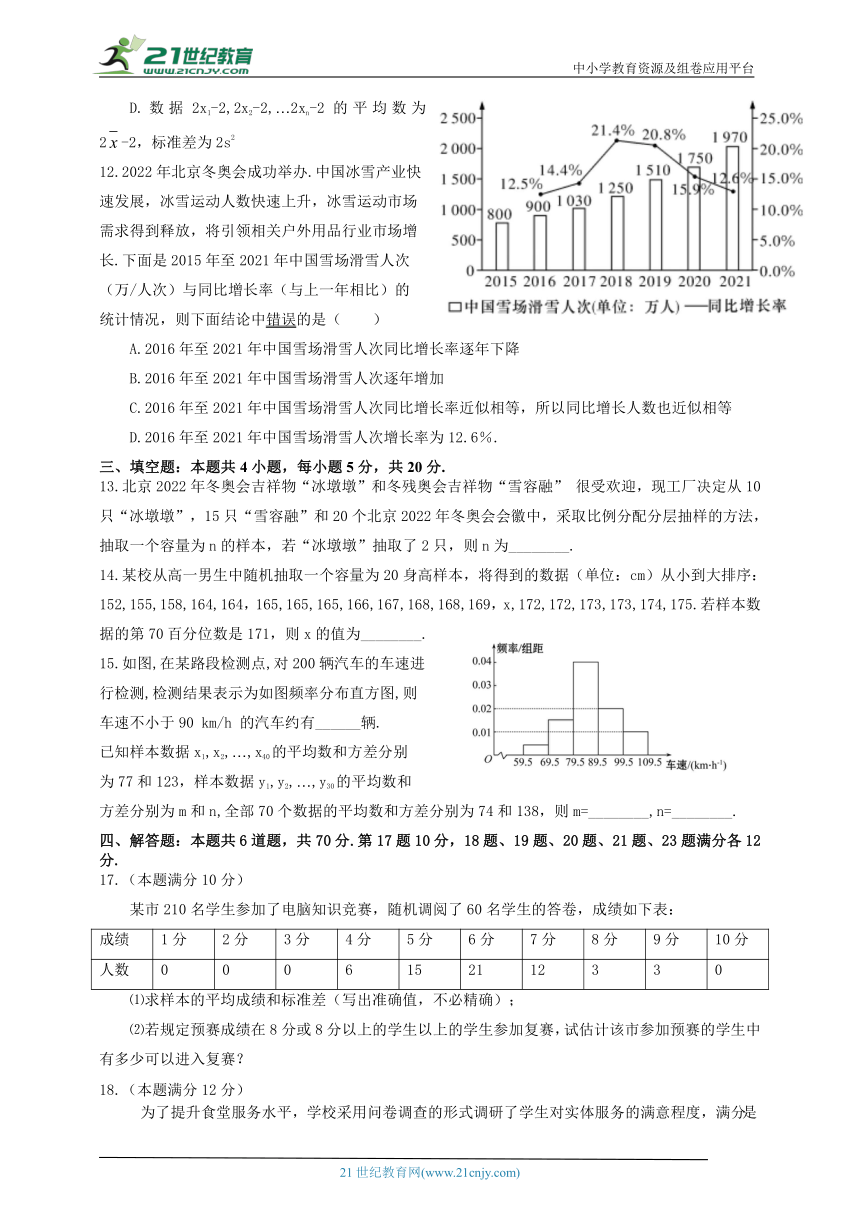
12.2022年北京冬奥会成功举办.中国冰雪产业快
速发展,冰雪运动人数快速上升,冰雪运动市场
需求得到释放,将引领相关户外用品行业市场增
长.下面是2015年至2021年中国雪场滑雪人次
(万/人次)与同比增长率(与上一年相比)的
统计情况,则下面结论中错误的是( )
A.2016年至2021年中国雪场滑雪人次同比增长率逐年下降
B.2016年至2021年中国雪场滑雪人次逐年增加
C.2016年至2021年中国雪场滑雪人次同比增长率近似相等,所以同比增长人数也近似相等
D.2016年至2021年中国雪场滑雪人次增长率为12.6%.
三、填空题:本题共4小题,每小题5分,共20分.
13.北京2022年冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融” 很受欢迎,现工厂决定从10只“冰墩墩”,15只“雪容融”和20个北京2022年冬奥会会徽中,采取比例分配分层抽样的方法,抽取一个容量为n的样本,若“冰墩墩”抽取了2只,则n为________.
14.某校从高一男生中随机抽取一个容量为20身高样本,将得到的数据(单位:cm)从小到大排序:152,155,158,164,164,165,165,165,166,167,168,168,169,x,172,172,173,173,174,175.若样本数据的第70百分位数是171,则x的值为________.
15.如图,在某路段检测点,对200辆汽车的车速进
行检测,检测结果表示为如图频率分布直方图,则
车速不小于90 km/h 的汽车约有______辆.
已知样本数据x1,x2,…,x40的平均数和方差分别
为77和123,样本数据y1,y2,…,y30的平均数和
方差分别为m和n,全部70个数据的平均数和方差分别为74和138,则m=________,n=________.
四、解答题:本题共6道题,共70分.第17题10分,18题、19题、20题、21题、23题满分各12分.
17.(本题满分10分)
某市210名学生参加了电脑知识竞赛,随机调阅了60名学生的答卷,成绩如下表:
成绩 1分 2分 3分 4分 5分 6分 7分 8分 9分 10分
人数 0 0 0 6 15 21 12 3 3 0
⑴求样本的平均成绩和标准差(写出准确值,不必精确);
⑵若规定预赛成绩在8分或8分以上的学生以上的学生参加复赛,试估计该市参加预赛的学生中有多少可以进入复赛?
18.(本题满分12分)
为了提升食堂服务水平,学校采用问卷调查的形式调研了学生对实体服务的满意程度,满分是100分将问卷回收并整理评分数据后,把得分
分成5组:[50,60),[60,70,),[70,80),
[80,90),[90,100],并绘制成如图所示的
频率直方图.
⑴计算a的值和样本平均分;
⑵为了更全面地了解师生对食堂服务水平的
评价,求该样本的50百分位数(精确到0.01)
19.(本题满分12分)
某行业主管部门为了了解该行业中小企业生产情况,随机抽查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
y的分组 [-0.2,0) [0,0.2) [0.2,0.4) [0.4,0.6) [0.6,0.8)
企业数 2 24 53 14 7
⑴分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;
⑵求这类企业产值增长率的平均数和标准差的估计值(同一组中的数据用该组区间的中点值代表).(精确到0.01) 附:≈8.602.
20.(本题满分12分)
对某班50人进行智力测验,其得分如下:
48,64,52,86,71,48,64,41,86,79,71,68,82,
84,68,64,62,68,81,57,90,52,74,73,56,78,
47,66,55,64,56,88,69,40,73,97,68,56,67,
59,70,52,79,44,55,69,62,58,32,58.
(1)这次测试成绩的最大值和最小值各是多少
(2)将[30,100)平分成7个小区间,试画出该班学生智力测验成绩的频数分布图.
(3)分析这个频数分布图,你能得出什么结论
21.(本题满分12分)
某校为了了解甲、乙两班的数学学习情况,从两班各抽出10名学生进行数学水平测试,成绩如下(单位:分):
甲班:82 84 85 89 79 80 91 89 79 74
乙班:90 76 86 81 84 87 86 82 85 83
(1)求两个样本的平均数;
(2)求两个样本的方差和标准差;
(3)试分析比较两个班的学习情况.
22.(本题满分12分)
某房产销售公司从登记购房的客户中随机选取了50名客户进行调查,按他们购一套房的价格(万元)分成6组:、、、、、得到频率分布直方图如图所示.
用频率估计概率.房产销售公司卖出一套房,房地产商给销售公司的佣金如下表(单位:万元):
每一套房价格区间
买一套房销售公司佣金收入 1 2 3 4 5 6
(1)求的值;
(2)求房产销售公司卖出一套房的平均佣金;
(3)该房产销售公司每月(按30天计)的销售成本占总佣金的百分比按下表分段累计计算:
月总佣金 销售成本占佣金比例
不超过100万元的部分 5%
超过100万元至200万元的部分 10%
超过200万元至300万元的部分 15%
超过300万元的部分 20%
若该销售公司平均每天销售4套房,请估计公司月利润(利润=总佣金-销售成本).
参考答案
一.选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.C 2.B 3.A 4.D 5.C 6.B 7.A 8.D
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分.
9.AD 10.BCD 11.BC 12.ACD
三、填空题:本题共4小题,每小题5分,共20分.
13. 9 14. 170 15. 60 16. 70,130.
四、解答题:本题共6道题,共70分.第17题10分,18题、19题、20题、21题、23题满分各12分.
17.解:⑴平均成绩为:(4×6+5×15+6×21+7×12+8×3+9×3)=6
方差s2=[6×(4-6)2+15×(5-6)2+21×(6-6)2+12×(7-6)2+3×(8-6)2+3×(9-6)2]=1.5.
标准差为
⑵在60名选手中,有3+3=6(名)学生预赛成绩在8分或8分以上,所以估计210名学生中,有21名学生成绩在8分或8分以上,故大约有21名学生进入复赛.
18.解:(1)由已知得20×a+0.15+0.2+0.55=1,得a=0.005
平均分=0.05×55+0.55×65+0.2×75+0.15×85+0.05×95=71
⑵设x为50百分位数,则由直方图可得0.05+(x-60)×0.055=0.5
解得x≈68.18.0
19.解:⑴根据产值增长率频数表得,所调查的100个企业中产值增长率不低于40%的企业比例为(14+7)÷100=0.21=21%,产值负增长的企业频率为2÷100=0.02=2%.
⑵企业产值增长率的平均数
=(-0.1×2+0.1×24+0.3×53+0.5×14+0.7×7)÷100=0.3=30%
产值增长率的方差s2=[(-0.4)2×2+(-0.2)2×24+02×53+0.22×14+0.42×7]÷100=0.0296.
产值增长率的标准差s==0.02×≈0.17
这类企业的产值增长率的平均数和标准差的估计值分别为0.30,0.17.
20.解:(1)最小值是32,最大值是97.
(2)7个区间分别是[30,40),[40,50),[50,60),[60,70),[70,80), [80,90),[90,100],每个小区间的长度是10,统计出各小区间内的数据频数,列表如下:
区间 [30,40) [40,50) [50,60) [60,70) [70,80) [80,90) [90,100)
频数 1 6 12 14 9 6 2
频数分布图如图所示.
(3)可以看出,该班智力测验成绩大体上呈两头小、中间大、左右对称的钟形状态,说明该班学生智力特别好或特别差的是极少数,而智力一般的是多数,这是一种最常见的分布.
21.解:(1)=×(82+84+85+89+79+80+91+89+79+74)=83. 2,
=×(90+76+86+81+84+87+86+82+85+83)=84.
(2)=×[(82-83.2)2+(84-83.2)2+(85-83.2)2+(89-83.2)2+(79-
83.2)2+(80-83.2)2+(91-83.2)2+(89-83.2)2+(79-83.2)2+(74-83.2)2]=
26. 36,
= [(90-84)2+(76-84)2+(86-84)2+(81-84)2+(84-84)2+(87-84)2+
(86-84)2+(82-84)2+(85-84)2+(83-84)2]=13. 2,
则s甲=≈5. 13,s乙=≈3. 63.
(3)因为<,所以甲班比乙班平均水平低.
因为s甲>s乙,所以甲班没有乙班稳定.
所以乙班的总体学习情况比甲班好.
22.解:(1)由50×(0.0008+0.0020+0.0024+0.0040+0.0048+a)=1得a=0.0060.
(2)设卖出一套房的平均佣金为万元,则
=1×0.002×50+2×0.004×50+3×0.006×50+×4×0.0048×50+5×0.0024×50+6×0.0008×50=32
⑶总佣金为3.2×4×30=384万元
月利润为y=384-(100×5%+100×10%+100×15%+84×20%)=384-46.8=337.2万元.
所以公司月利润为337.2万元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第九章统计章末检测试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷解答题又分必考题和选考题两部分,选考题为二选一.考生作答时,将所有答案写在答题卡上,在本试卷上答题无效.本试卷满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.
2.选择题答案使用2AB铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,书写要工整、笔迹清楚,将答案书写在答题卡规定的位置上.
3.所有题目必须在答题卡上作答,在试卷上答题无效.
第Ⅰ卷 (选择题共60分)
一.选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.学校组织班级安全知识竞赛,某班的12名学生的成绩(单位:分)分别是:58,67,73,75,76,82,82,
87,90,92,93,98,则这12名学生成绩的第一四分位数是( )
72分 B. 73分 C. 74分 D.75分
2.已知某工厂生产A,B,C三种不同型号的产品,某月生产A,B,C这三种型号的产品的数量之比为1:a:2,现用分层抽样的方法抽取一个容量为60的样本,已知B型号产品被抽出30件,则a的值为( )
A. 4 B. 3 C. 2 D. 1
3.已知数据x1,x2,…,x30的极差为6,方差为2,则数据2x1+1,2x2+1,…,2x30+1的极差和方差分别为( )
A. 18,2 B. 12,4 C. 6,8 D. 6,4
4.在简单随机抽样中,某一个个体被抽到的概率( )
A.与第几次抽样有关,第一次被抽到的概率最大 B.与第几次抽样有关,第一次被抽到的概率最小
C.与第几次抽样无关,每一次被抽到的概率相等 D.与第几次抽样无关,与抽取几个样本有关
5.根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精含量在
80 mg/100 mL以上(含80)时,属醉酒驾车.某地对涉嫌酒
后驾车的28800人进行血液检测,根据检测结果绘制的频
率分布直方图如图.则这28800人中属于醉酒驾车的人数
约为( )
A.8 640 B.5 760
C.4 320 D.2 880
6.北京冬奥会已于2022年2月4日至2月20日顺利举行,这是中国继北京奥运会,南京青奥会后,第三次举办的奥运赛事.之前,为助力冬奥,提高群众奥运法律知识水平和文明素质,某市有关部门开展冬奥法律知识普及线上答题,共计30道题,每道题2分,满分60分.现从参与线上答题的市民中随机抽取1000名,将他们的作答成绩分成6组,并绘制了如图所示的频率分布直方图.若同一组中的数据用
该组区间中点值为代表,可估计这次线上答题成
绩的平均数为( )
33 B. 34
C. 35 D. 36
7.某班有50名学生,在一次考试中统计出平均分数为
70,方差为75,后来发现有2名学生的成绩统计有误,学
生甲实际得分是80分却误记为60分,学生乙实际得分是70分却误记为90分,更正后的平均分数和方差分别是( )
A.70和67 B.70和50 C.75和50 D.75和67
8.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.两组工人完成生产任务的工作时间(单位:min)为:
第一种生产方式:68,72,76,77,79,82,83,83,84,85,86,87,87,88,89,90,
90,91,91,92
第二种生产方式:65,65,66,68,69,70,71,72,72,73,74,75,76,76,78,81,
84,84,85,90
则下列结论中,表述不正确的是( )
A.第一种生产方式的工人中,有75%的工人完成生产任务所需要的时间至少80 min
B.第二种生产方式比第一种生产方式的效率更高
C.这40名工人完成任务所需时间的中位数为80 min
D.无论哪种生产方式的工人完成生产任务平均所需要的时间都是80 min
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分.
9.关于简单随机抽样,下列说法正确的是( )
A.它要求被抽取样本的总体的个数有限 B.它是从总体中逐个地进行抽取
C.它是一种不放回抽样 D.它是一种等可能性抽样
10.某校高一800名学生参加了数学检测,
将所有学生的数学成绩分组如下:[90,100),
[100,110),[110,120),[120,130),[130,140),
[140,150],得到的频率分布直方图如图所示,
下列说法中正确的是( )
A.成绩不低于120分的学生人数为1220.
B.这800名学生中数学成绩的众数为125.
C.若本次测试合格率定为60%,则至少得118分才能合格.
D.这800名学生数学成绩的平均数为12
11. 已知数据x1,x2,…,xn的平均数为,标准差为s2,则( )
A.数据x12,x22,…,xn2的平均数为,标准差为s2
B.数据2x1,2x2,…,2xn的平均数为2,标准差为2s
C.数据,x1+2,x2+2,…,xn+2的平均数为+2,标准差为s2
D.数据2x1-2,2x2-2,…2xn-2的平均数为2-2,标准差为2s2
12.2022年北京冬奥会成功举办.中国冰雪产业快
速发展,冰雪运动人数快速上升,冰雪运动市场
需求得到释放,将引领相关户外用品行业市场增
长.下面是2015年至2021年中国雪场滑雪人次
(万/人次)与同比增长率(与上一年相比)的
统计情况,则下面结论中错误的是( )
A.2016年至2021年中国雪场滑雪人次同比增长率逐年下降
B.2016年至2021年中国雪场滑雪人次逐年增加
C.2016年至2021年中国雪场滑雪人次同比增长率近似相等,所以同比增长人数也近似相等
D.2016年至2021年中国雪场滑雪人次增长率为12.6%.
三、填空题:本题共4小题,每小题5分,共20分.
13.北京2022年冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融” 很受欢迎,现工厂决定从10只“冰墩墩”,15只“雪容融”和20个北京2022年冬奥会会徽中,采取比例分配分层抽样的方法,抽取一个容量为n的样本,若“冰墩墩”抽取了2只,则n为________.
14.某校从高一男生中随机抽取一个容量为20身高样本,将得到的数据(单位:cm)从小到大排序:152,155,158,164,164,165,165,165,166,167,168,168,169,x,172,172,173,173,174,175.若样本数据的第70百分位数是171,则x的值为________.
15.如图,在某路段检测点,对200辆汽车的车速进
行检测,检测结果表示为如图频率分布直方图,则
车速不小于90 km/h 的汽车约有______辆.
已知样本数据x1,x2,…,x40的平均数和方差分别
为77和123,样本数据y1,y2,…,y30的平均数和
方差分别为m和n,全部70个数据的平均数和方差分别为74和138,则m=________,n=________.
四、解答题:本题共6道题,共70分.第17题10分,18题、19题、20题、21题、23题满分各12分.
17.(本题满分10分)
某市210名学生参加了电脑知识竞赛,随机调阅了60名学生的答卷,成绩如下表:
成绩 1分 2分 3分 4分 5分 6分 7分 8分 9分 10分
人数 0 0 0 6 15 21 12 3 3 0
⑴求样本的平均成绩和标准差(写出准确值,不必精确);
⑵若规定预赛成绩在8分或8分以上的学生以上的学生参加复赛,试估计该市参加预赛的学生中有多少可以进入复赛?
18.(本题满分12分)
为了提升食堂服务水平,学校采用问卷调查的形式调研了学生对实体服务的满意程度,满分是100分将问卷回收并整理评分数据后,把得分
分成5组:[50,60),[60,70,),[70,80),
[80,90),[90,100],并绘制成如图所示的
频率直方图.
⑴计算a的值和样本平均分;
⑵为了更全面地了解师生对食堂服务水平的
评价,求该样本的50百分位数(精确到0.01)
19.(本题满分12分)
某行业主管部门为了了解该行业中小企业生产情况,随机抽查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
y的分组 [-0.2,0) [0,0.2) [0.2,0.4) [0.4,0.6) [0.6,0.8)
企业数 2 24 53 14 7
⑴分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;
⑵求这类企业产值增长率的平均数和标准差的估计值(同一组中的数据用该组区间的中点值代表).(精确到0.01) 附:≈8.602.
20.(本题满分12分)
对某班50人进行智力测验,其得分如下:
48,64,52,86,71,48,64,41,86,79,71,68,82,
84,68,64,62,68,81,57,90,52,74,73,56,78,
47,66,55,64,56,88,69,40,73,97,68,56,67,
59,70,52,79,44,55,69,62,58,32,58.
(1)这次测试成绩的最大值和最小值各是多少
(2)将[30,100)平分成7个小区间,试画出该班学生智力测验成绩的频数分布图.
(3)分析这个频数分布图,你能得出什么结论
21.(本题满分12分)
某校为了了解甲、乙两班的数学学习情况,从两班各抽出10名学生进行数学水平测试,成绩如下(单位:分):
甲班:82 84 85 89 79 80 91 89 79 74
乙班:90 76 86 81 84 87 86 82 85 83
(1)求两个样本的平均数;
(2)求两个样本的方差和标准差;
(3)试分析比较两个班的学习情况.
22.(本题满分12分)
某房产销售公司从登记购房的客户中随机选取了50名客户进行调查,按他们购一套房的价格(万元)分成6组:、、、、、得到频率分布直方图如图所示.
用频率估计概率.房产销售公司卖出一套房,房地产商给销售公司的佣金如下表(单位:万元):
每一套房价格区间
买一套房销售公司佣金收入 1 2 3 4 5 6
(1)求的值;
(2)求房产销售公司卖出一套房的平均佣金;
(3)该房产销售公司每月(按30天计)的销售成本占总佣金的百分比按下表分段累计计算:
月总佣金 销售成本占佣金比例
不超过100万元的部分 5%
超过100万元至200万元的部分 10%
超过200万元至300万元的部分 15%
超过300万元的部分 20%
若该销售公司平均每天销售4套房,请估计公司月利润(利润=总佣金-销售成本).
参考答案
一.选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.C 2.B 3.A 4.D 5.C 6.B 7.A 8.D
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分.
9.AD 10.BCD 11.BC 12.ACD
三、填空题:本题共4小题,每小题5分,共20分.
13. 9 14. 170 15. 60 16. 70,130.
四、解答题:本题共6道题,共70分.第17题10分,18题、19题、20题、21题、23题满分各12分.
17.解:⑴平均成绩为:(4×6+5×15+6×21+7×12+8×3+9×3)=6
方差s2=[6×(4-6)2+15×(5-6)2+21×(6-6)2+12×(7-6)2+3×(8-6)2+3×(9-6)2]=1.5.
标准差为
⑵在60名选手中,有3+3=6(名)学生预赛成绩在8分或8分以上,所以估计210名学生中,有21名学生成绩在8分或8分以上,故大约有21名学生进入复赛.
18.解:(1)由已知得20×a+0.15+0.2+0.55=1,得a=0.005
平均分=0.05×55+0.55×65+0.2×75+0.15×85+0.05×95=71
⑵设x为50百分位数,则由直方图可得0.05+(x-60)×0.055=0.5
解得x≈68.18.0
19.解:⑴根据产值增长率频数表得,所调查的100个企业中产值增长率不低于40%的企业比例为(14+7)÷100=0.21=21%,产值负增长的企业频率为2÷100=0.02=2%.
⑵企业产值增长率的平均数
=(-0.1×2+0.1×24+0.3×53+0.5×14+0.7×7)÷100=0.3=30%
产值增长率的方差s2=[(-0.4)2×2+(-0.2)2×24+02×53+0.22×14+0.42×7]÷100=0.0296.
产值增长率的标准差s==0.02×≈0.17
这类企业的产值增长率的平均数和标准差的估计值分别为0.30,0.17.
20.解:(1)最小值是32,最大值是97.
(2)7个区间分别是[30,40),[40,50),[50,60),[60,70),[70,80), [80,90),[90,100],每个小区间的长度是10,统计出各小区间内的数据频数,列表如下:
区间 [30,40) [40,50) [50,60) [60,70) [70,80) [80,90) [90,100)
频数 1 6 12 14 9 6 2
频数分布图如图所示.
(3)可以看出,该班智力测验成绩大体上呈两头小、中间大、左右对称的钟形状态,说明该班学生智力特别好或特别差的是极少数,而智力一般的是多数,这是一种最常见的分布.
21.解:(1)=×(82+84+85+89+79+80+91+89+79+74)=83. 2,
=×(90+76+86+81+84+87+86+82+85+83)=84.
(2)=×[(82-83.2)2+(84-83.2)2+(85-83.2)2+(89-83.2)2+(79-
83.2)2+(80-83.2)2+(91-83.2)2+(89-83.2)2+(79-83.2)2+(74-83.2)2]=
26. 36,
= [(90-84)2+(76-84)2+(86-84)2+(81-84)2+(84-84)2+(87-84)2+
(86-84)2+(82-84)2+(85-84)2+(83-84)2]=13. 2,
则s甲=≈5. 13,s乙=≈3. 63.
(3)因为<,所以甲班比乙班平均水平低.
因为s甲>s乙,所以甲班没有乙班稳定.
所以乙班的总体学习情况比甲班好.
22.解:(1)由50×(0.0008+0.0020+0.0024+0.0040+0.0048+a)=1得a=0.0060.
(2)设卖出一套房的平均佣金为万元,则
=1×0.002×50+2×0.004×50+3×0.006×50+×4×0.0048×50+5×0.0024×50+6×0.0008×50=32
⑶总佣金为3.2×4×30=384万元
月利润为y=384-(100×5%+100×10%+100×15%+84×20%)=384-46.8=337.2万元.
所以公司月利润为337.2万元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
