鲁教版九年级数学上册第一单元1.5解直角三角形的应用(4课时)
文档属性
| 名称 | 鲁教版九年级数学上册第一单元1.5解直角三角形的应用(4课时) |  | |
| 格式 | zip | ||
| 文件大小 | 313.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-01 00:00:02 | ||
图片预览

文档简介
鲁教版九年级数学上册第一单元1.5解直角三角形的应用(第1课时)
学习目标:
能把实际问题转化为数学问题的能力。
使学生认识数学与生产生活的联系,养成应用数学的意识,激发学习的兴趣和求知欲望。
学习重难点:理解坡角的概念,能用利用解直角三角形的知识解决问题。
学习过程
一、知识衔接
1、在Rt△ABC中,sinA= ,cosA= ______,tanA= 。
二、例题学习
例1、当登山缆车的吊箱经过点A到达点B时,它走过了200 m。已知缆车的路线与平面的夹角为∠A=16°,那么缆车垂直上升的距离是多少
问题:(1)哪条线段代表缆车上升的垂直距离
(2)利用哪个直角三角形可以求出BC
当缆车由点B到达点D时,它又走过了200m,缆车由B到达D的行驶路线与水平面的夹角∠β=42°,由此,你能求出缆车又垂直上升的距离是多少
例2 一个小孩荡秋千,秋千链子的长度为2 ( http: / / www.21cnjy.com ).5米,当秋千前后摆动时,摆角恰好为60°,且前后摆动的角度相同。求它摆至最高位置时与其至最低位置时的高度之差(结果精确到0.01米)
三、随堂练习
1、一个人由山底爬到山顶,需先爬45°的山坡300 m,再爬30°的山坡100 m,求山高。
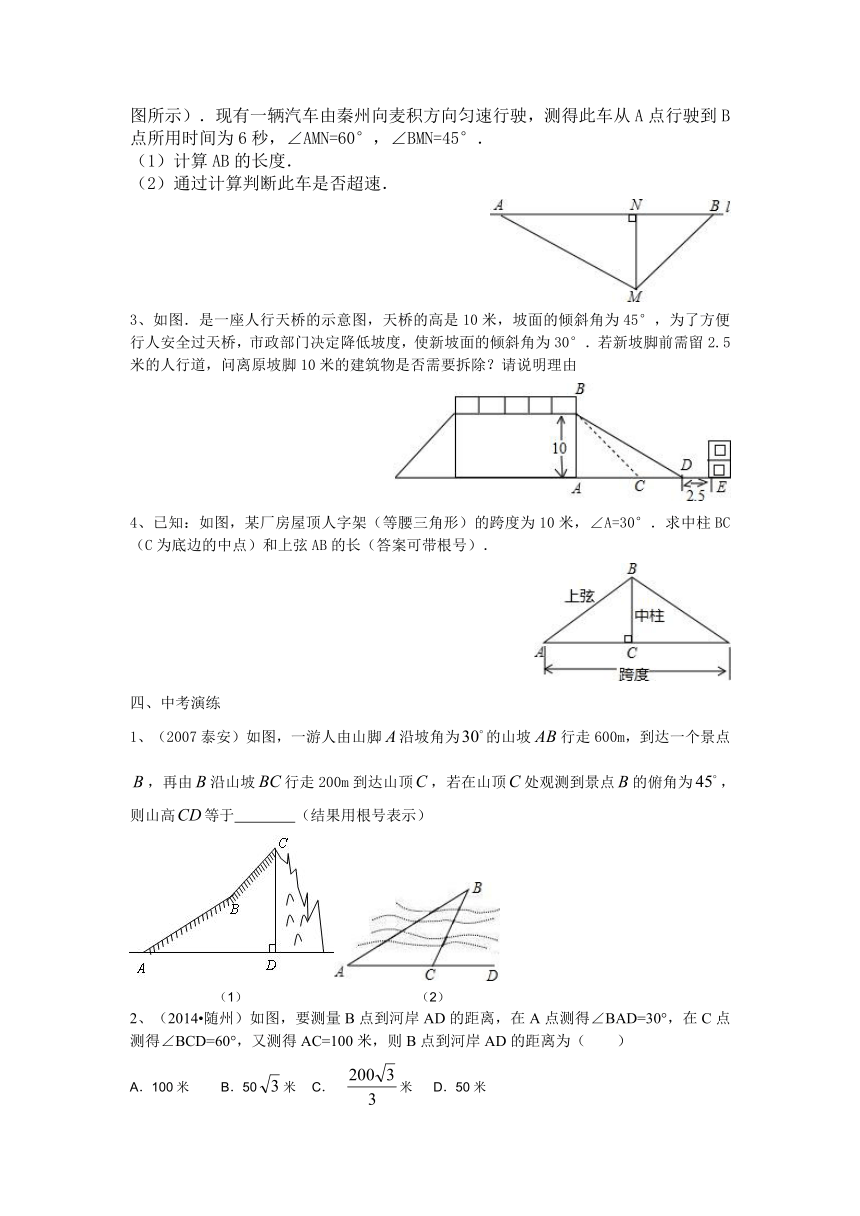
2、(2014 天水)根据道路管理规定,在 ( http: / / www.21cnjy.com )羲皇大道秦州至麦积段上行驶的车辆,限速60千米/时.已知测速站点M距羲皇大道l(直线)的距离MN为30米(如图所示).现有一辆汽车由秦州向麦积方向匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°.
(1)计算AB的长度.
(2)通过计算判断此车是否超速.
3、如图.是一座人行天桥的示意图,天桥的高 ( http: / / www.21cnjy.com )是10米,坡面的倾斜角为45°,为了方便行人安全过天桥,市政部门决定降低坡度,使新坡面的倾斜角为30°.若新坡脚前需留2.5米的人行道,问离原坡脚10米的建筑物是否需要拆除?请说明理由
4、已知:如图,某厂房屋顶人字架(等腰三角形)的跨度为10米,∠A=30°.求中柱BC(C为底边的中点)和上弦AB的长(答案可带根号).
四、中考演练
1、(2007泰安)如图,一游人由山脚沿坡角为的山坡行走600m,到达一个景点,再由沿山坡行走200m到达山顶,若在山顶处观测到景点的俯角为,则山高等于 (结果用根号表示)
( http: / / www.21cnjy.com )
(1) (2)
2、(2014 随州)如图 ( http: / / www.21cnjy.com ),要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )
A.100米 B.50米 C. 米 D.50米
鲁教版九年级数学上册第一单元1.5解直角三角形的应用(第2课时)
学习目标:
1、了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.
2、逐步培养分析问题、解决问题的能力.
学习重难点:
1、将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.
2、学习实际问题转化成数学模型
学习过程
一、学习新知
1、仰角、俯角的理解
当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.
二、例题学习
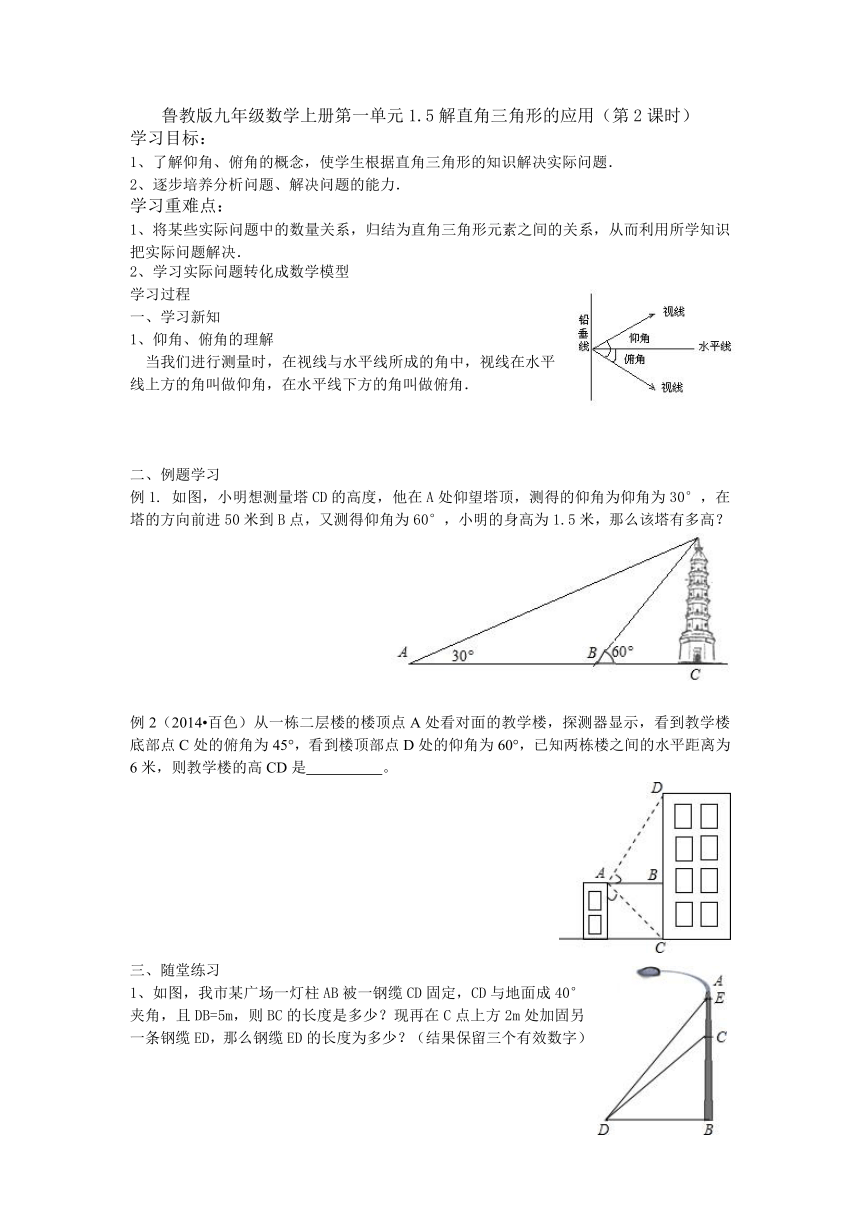
例1. 如图,小明想测量塔CD的高度, ( http: / / www.21cnjy.com )他在A处仰望塔顶,测得的仰角为仰角为30°,在塔的方向前进50米到B点,又测得仰角为60°,小明的身高为1.5米,那么该塔有多高?
( http: / / www.21cnjy.com )
例2(2014 百色)从一栋二层楼 ( http: / / www.21cnjy.com )的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是 。
三、随堂练习
1、如图,我市某广场一灯柱AB被一 ( http: / / www.21cnjy.com )钢缆CD固定,CD与地面成40°夹角,且DB=5m,则BC的长度是多少?现再在C点上方2m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果保留三个有效数字)
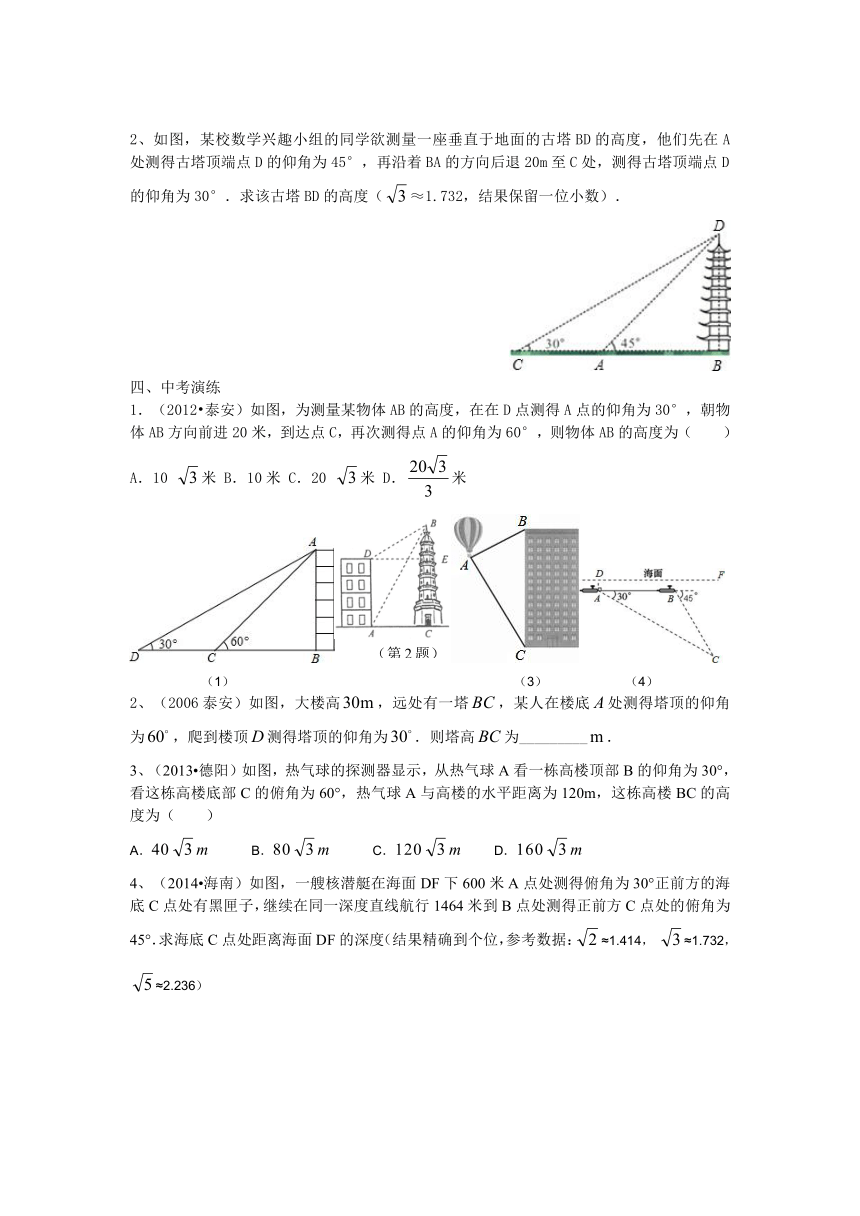
2、如图,某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退20m至C处,测得古塔顶端点D的仰角为30°.求该古塔BD的高度(≈1.732,结果保留一位小数).
四、中考演练
1.(2012 泰安)如图,为测量某物体AB ( http: / / www.21cnjy.com )的高度,在在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A.10 米 B.10米 C.20 米 D.米
(1) (3) (4)
2、(2006泰安)如图,大楼高,远处有一塔,某人在楼底处测得塔顶的仰角为,爬到楼顶测得塔顶的仰角为.则塔高为_________.
3、(2013 德阳)如图 ( http: / / www.21cnjy.com ),热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )
A.40m B.80m C.120m D.160m
4、(2014 海南)如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:≈1.414, ≈1.732, ≈2.236)
鲁教版九年级数学上册第一单元1.5解直角三角形的应用(第3课时)
学习目标:
1、弄清题中的名词、术语的意义,方位角,然后根据题意画出几何图形,建立数学模型
2、适当的选择锐角三角函数关系式去解决直角三角形问题;
学习重难点:
1、弄清题中的名词、术语的意义。
2、会利用解直角三角形的知识。
学习过程
一、课前热身
1、小宁想知道校园内一棵大树的高度(如图),他测得CB的长度为10米,∠ACB=60°,请你帮他算出树高AB约为 米.
(1) (2) (3)
2、如图,一辆汽车沿着坡度为i=1:的斜坡向下行驶50米,则它距离地面的垂直高度下降了 米.
3、张华同学在学校某建筑物的C点处测得旗杆顶部A点的仰角为30°,旗杆底部B点的俯角为45°.若旗杆底部B点到建筑物的水平距离BE=9米,旗杆台阶高1米,则旗杆顶点A离地面的高度为多少米?(精确到0.1米,≈1.732)
二、例题学习
1、如图一轮船自西向东航 ( http: / / www.21cnjy.com )行,在A处测得某岛C,在北偏东60°的方向上,船前进8海里后到达B,再测C岛,在北偏东30°的方向上,问船再前进多少海里与C岛最近 最近距离是多少
例2.如图所示,海上有一灯塔P,在它周 ( http: / / www.21cnjy.com )围3海里处有暗礁.一艘客轮以9海里/时?的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向.问客轮不改变方向继续前进有无触礁的危险
三、随堂练习
1、上午10点整,一渔轮在小岛O的北偏 ( http: / / www.21cnjy.com )东30°方向,距离等于10海里的A处,正以每小时10海里的速度向南偏东60°方向航行.那么渔轮到达小岛O的正东方向是什么时间?(精确到1分).
( http: / / www.21cnjy.com )
2、(2014 南通)如图,海中有 ( http: / / www.21cnjy.com )一灯塔P,它的周围8海里内有暗礁.海伦以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东60°方向上;航行40分钟到达B处,测得灯塔P在北偏东30°方向上;如果海轮不改变航线继续向东航行,有没有触礁的危险?
四、中考演练
1、(2009泰安)在一次夏令营活动中, ( http: / / www.21cnjy.com )小亮从位于A点的营地出发,沿北偏东60°方向走了5km到达B地,然后再沿北偏西30°方向走了若干千米到达C地,测得A地在C地南偏西30°方向,则A、C两地的距离为
(A) (B)(C) (D)
2、(2013 泰安)如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向,海监船航行到B处时望见渔船D在南偏东45°方向,又航行了半小时到达C处,望见渔船D在南偏东60°方向,若海监船的速度为50海里/小时,则A,B之间的距离为 _________ (取,结果精确到0.1海里).
( http: / / www.21cnjy.com )
鲁教版九年级数学上册第一单元1.5解直角三角形的应用(第4课时)
学习目标
1.使学生理解坡角、坡比等概念的意义,并能解决有关实际问题;
2.使学生能适当的选择锐角三角函数关系式去解决直角三角形问题;
学习重难点
1、用三角函数有关知识解决方位角和坡角、坡比的实际问题
2、学会准确分析问题并将实际问题转化成数学模型
学习过程
一、学习新知
1、 坡面的铅直高度h和水平宽度的比叫做坡度(或叫做坡比),
2、一般用i表示。即i=( )常写成i=1:m的形式如i=1:2.5把坡面与水平面的夹角α叫做坡角.
结合图形思考,坡度i与坡角α之间具有什么关系?
3、即学即用:(1)一段坡面的坡角为60°,则坡度i=______;
______,坡角______度
二、例题学习
例1,如图,水库大坝的横截面是梯形, ( http: / / www.21cnjy.com )坝顶宽6m, 坝高23m, 斜坡AB的坡度i=1:3, 斜坡CD的坡度i=1:2.5, 求斜坡AB的坡角a,坝底宽AD 和斜坡AB的长(精确到0.1米)
分析:此题应正确理解,将实际问题转化为 ( http: / / www.21cnjy.com )数学问题,应用坡度、坡角的概念及联系,即i=tanα= ,将梯形问题,添加高线把梯形转化为 来解.
例2、如图,水库的大坝横截面是一个梯形ABCD,坝顶宽AD=6m,坝高5m,斜坡CD=8m,坝底BC=30m,∠ADC=135°,
(1)求∠ABC的度数;
(2)如果坝长100米,那么建筑这个大坝共需多少石料?
三、随堂练习
1、(2014 德州)如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为 。
(1) (2)
2、(2014 普宁市模拟)某河坝横截面如图,堤高BC=6米,迎水坡AB=6米,则迎水坡AB的坡度为( )
3、某海港区为提高某段海堤的防海潮能力,计划将100米的一段堤(原海堤的横断面如图中的梯形ABCD)的堤面加宽1米,背水坡度由原来的1:1改成1:2。已知原背水坡长AD= 米,求完成这一工程所需的土方数。
( http: / / www.21cnjy.com )
四、中考链接
1.(2014 射阳县三模)小 ( http: / / www.21cnjy.com )明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡度为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,求树的高度.
2、(2014 巴中)如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30°,求坝底AD的长度.(精确到0.1米,参考数据: ≈1.414, ≈1.732.提示:坡度等于坡面的铅垂高度与水平长度之比).
(第2题)
第1题图
学习目标:
能把实际问题转化为数学问题的能力。
使学生认识数学与生产生活的联系,养成应用数学的意识,激发学习的兴趣和求知欲望。
学习重难点:理解坡角的概念,能用利用解直角三角形的知识解决问题。
学习过程
一、知识衔接
1、在Rt△ABC中,sinA= ,cosA= ______,tanA= 。
二、例题学习
例1、当登山缆车的吊箱经过点A到达点B时,它走过了200 m。已知缆车的路线与平面的夹角为∠A=16°,那么缆车垂直上升的距离是多少
问题:(1)哪条线段代表缆车上升的垂直距离
(2)利用哪个直角三角形可以求出BC
当缆车由点B到达点D时,它又走过了200m,缆车由B到达D的行驶路线与水平面的夹角∠β=42°,由此,你能求出缆车又垂直上升的距离是多少
例2 一个小孩荡秋千,秋千链子的长度为2 ( http: / / www.21cnjy.com ).5米,当秋千前后摆动时,摆角恰好为60°,且前后摆动的角度相同。求它摆至最高位置时与其至最低位置时的高度之差(结果精确到0.01米)
三、随堂练习
1、一个人由山底爬到山顶,需先爬45°的山坡300 m,再爬30°的山坡100 m,求山高。
2、(2014 天水)根据道路管理规定,在 ( http: / / www.21cnjy.com )羲皇大道秦州至麦积段上行驶的车辆,限速60千米/时.已知测速站点M距羲皇大道l(直线)的距离MN为30米(如图所示).现有一辆汽车由秦州向麦积方向匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°.
(1)计算AB的长度.
(2)通过计算判断此车是否超速.
3、如图.是一座人行天桥的示意图,天桥的高 ( http: / / www.21cnjy.com )是10米,坡面的倾斜角为45°,为了方便行人安全过天桥,市政部门决定降低坡度,使新坡面的倾斜角为30°.若新坡脚前需留2.5米的人行道,问离原坡脚10米的建筑物是否需要拆除?请说明理由
4、已知:如图,某厂房屋顶人字架(等腰三角形)的跨度为10米,∠A=30°.求中柱BC(C为底边的中点)和上弦AB的长(答案可带根号).
四、中考演练
1、(2007泰安)如图,一游人由山脚沿坡角为的山坡行走600m,到达一个景点,再由沿山坡行走200m到达山顶,若在山顶处观测到景点的俯角为,则山高等于 (结果用根号表示)
( http: / / www.21cnjy.com )
(1) (2)
2、(2014 随州)如图 ( http: / / www.21cnjy.com ),要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )
A.100米 B.50米 C. 米 D.50米
鲁教版九年级数学上册第一单元1.5解直角三角形的应用(第2课时)
学习目标:
1、了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.
2、逐步培养分析问题、解决问题的能力.
学习重难点:
1、将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.
2、学习实际问题转化成数学模型
学习过程
一、学习新知
1、仰角、俯角的理解
当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.
二、例题学习
例1. 如图,小明想测量塔CD的高度, ( http: / / www.21cnjy.com )他在A处仰望塔顶,测得的仰角为仰角为30°,在塔的方向前进50米到B点,又测得仰角为60°,小明的身高为1.5米,那么该塔有多高?
( http: / / www.21cnjy.com )
例2(2014 百色)从一栋二层楼 ( http: / / www.21cnjy.com )的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是 。
三、随堂练习
1、如图,我市某广场一灯柱AB被一 ( http: / / www.21cnjy.com )钢缆CD固定,CD与地面成40°夹角,且DB=5m,则BC的长度是多少?现再在C点上方2m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果保留三个有效数字)
2、如图,某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退20m至C处,测得古塔顶端点D的仰角为30°.求该古塔BD的高度(≈1.732,结果保留一位小数).
四、中考演练
1.(2012 泰安)如图,为测量某物体AB ( http: / / www.21cnjy.com )的高度,在在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A.10 米 B.10米 C.20 米 D.米
(1) (3) (4)
2、(2006泰安)如图,大楼高,远处有一塔,某人在楼底处测得塔顶的仰角为,爬到楼顶测得塔顶的仰角为.则塔高为_________.
3、(2013 德阳)如图 ( http: / / www.21cnjy.com ),热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )
A.40m B.80m C.120m D.160m
4、(2014 海南)如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:≈1.414, ≈1.732, ≈2.236)
鲁教版九年级数学上册第一单元1.5解直角三角形的应用(第3课时)
学习目标:
1、弄清题中的名词、术语的意义,方位角,然后根据题意画出几何图形,建立数学模型
2、适当的选择锐角三角函数关系式去解决直角三角形问题;
学习重难点:
1、弄清题中的名词、术语的意义。
2、会利用解直角三角形的知识。
学习过程
一、课前热身
1、小宁想知道校园内一棵大树的高度(如图),他测得CB的长度为10米,∠ACB=60°,请你帮他算出树高AB约为 米.
(1) (2) (3)
2、如图,一辆汽车沿着坡度为i=1:的斜坡向下行驶50米,则它距离地面的垂直高度下降了 米.
3、张华同学在学校某建筑物的C点处测得旗杆顶部A点的仰角为30°,旗杆底部B点的俯角为45°.若旗杆底部B点到建筑物的水平距离BE=9米,旗杆台阶高1米,则旗杆顶点A离地面的高度为多少米?(精确到0.1米,≈1.732)
二、例题学习
1、如图一轮船自西向东航 ( http: / / www.21cnjy.com )行,在A处测得某岛C,在北偏东60°的方向上,船前进8海里后到达B,再测C岛,在北偏东30°的方向上,问船再前进多少海里与C岛最近 最近距离是多少
例2.如图所示,海上有一灯塔P,在它周 ( http: / / www.21cnjy.com )围3海里处有暗礁.一艘客轮以9海里/时?的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向.问客轮不改变方向继续前进有无触礁的危险
三、随堂练习
1、上午10点整,一渔轮在小岛O的北偏 ( http: / / www.21cnjy.com )东30°方向,距离等于10海里的A处,正以每小时10海里的速度向南偏东60°方向航行.那么渔轮到达小岛O的正东方向是什么时间?(精确到1分).
( http: / / www.21cnjy.com )
2、(2014 南通)如图,海中有 ( http: / / www.21cnjy.com )一灯塔P,它的周围8海里内有暗礁.海伦以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东60°方向上;航行40分钟到达B处,测得灯塔P在北偏东30°方向上;如果海轮不改变航线继续向东航行,有没有触礁的危险?
四、中考演练
1、(2009泰安)在一次夏令营活动中, ( http: / / www.21cnjy.com )小亮从位于A点的营地出发,沿北偏东60°方向走了5km到达B地,然后再沿北偏西30°方向走了若干千米到达C地,测得A地在C地南偏西30°方向,则A、C两地的距离为
(A) (B)(C) (D)
2、(2013 泰安)如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向,海监船航行到B处时望见渔船D在南偏东45°方向,又航行了半小时到达C处,望见渔船D在南偏东60°方向,若海监船的速度为50海里/小时,则A,B之间的距离为 _________ (取,结果精确到0.1海里).
( http: / / www.21cnjy.com )
鲁教版九年级数学上册第一单元1.5解直角三角形的应用(第4课时)
学习目标
1.使学生理解坡角、坡比等概念的意义,并能解决有关实际问题;
2.使学生能适当的选择锐角三角函数关系式去解决直角三角形问题;
学习重难点
1、用三角函数有关知识解决方位角和坡角、坡比的实际问题
2、学会准确分析问题并将实际问题转化成数学模型
学习过程
一、学习新知
1、 坡面的铅直高度h和水平宽度的比叫做坡度(或叫做坡比),
2、一般用i表示。即i=( )常写成i=1:m的形式如i=1:2.5把坡面与水平面的夹角α叫做坡角.
结合图形思考,坡度i与坡角α之间具有什么关系?
3、即学即用:(1)一段坡面的坡角为60°,则坡度i=______;
______,坡角______度
二、例题学习
例1,如图,水库大坝的横截面是梯形, ( http: / / www.21cnjy.com )坝顶宽6m, 坝高23m, 斜坡AB的坡度i=1:3, 斜坡CD的坡度i=1:2.5, 求斜坡AB的坡角a,坝底宽AD 和斜坡AB的长(精确到0.1米)
分析:此题应正确理解,将实际问题转化为 ( http: / / www.21cnjy.com )数学问题,应用坡度、坡角的概念及联系,即i=tanα= ,将梯形问题,添加高线把梯形转化为 来解.
例2、如图,水库的大坝横截面是一个梯形ABCD,坝顶宽AD=6m,坝高5m,斜坡CD=8m,坝底BC=30m,∠ADC=135°,
(1)求∠ABC的度数;
(2)如果坝长100米,那么建筑这个大坝共需多少石料?
三、随堂练习
1、(2014 德州)如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为 。
(1) (2)
2、(2014 普宁市模拟)某河坝横截面如图,堤高BC=6米,迎水坡AB=6米,则迎水坡AB的坡度为( )
3、某海港区为提高某段海堤的防海潮能力,计划将100米的一段堤(原海堤的横断面如图中的梯形ABCD)的堤面加宽1米,背水坡度由原来的1:1改成1:2。已知原背水坡长AD= 米,求完成这一工程所需的土方数。
( http: / / www.21cnjy.com )
四、中考链接
1.(2014 射阳县三模)小 ( http: / / www.21cnjy.com )明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡度为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,求树的高度.
2、(2014 巴中)如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30°,求坝底AD的长度.(精确到0.1米,参考数据: ≈1.414, ≈1.732.提示:坡度等于坡面的铅垂高度与水平长度之比).
(第2题)
第1题图
