从梯子和倾斜程度谈起---正切函数习题课[下学期]
文档属性
| 名称 | 从梯子和倾斜程度谈起---正切函数习题课[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 93.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-12-02 00:00:00 | ||
图片预览




文档简介
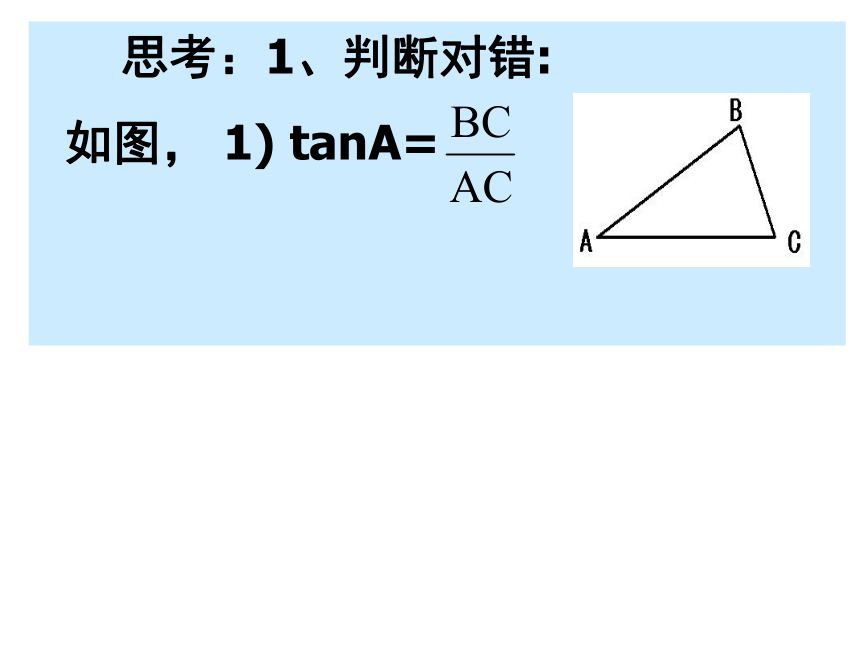
课件20张PPT。正切函数 在直角三角形中,若一个锐角的对边与邻边的比值是一个定值,那么这个角的值也随之确定。 思考:1、判断对错:
如图, 1) tanA=
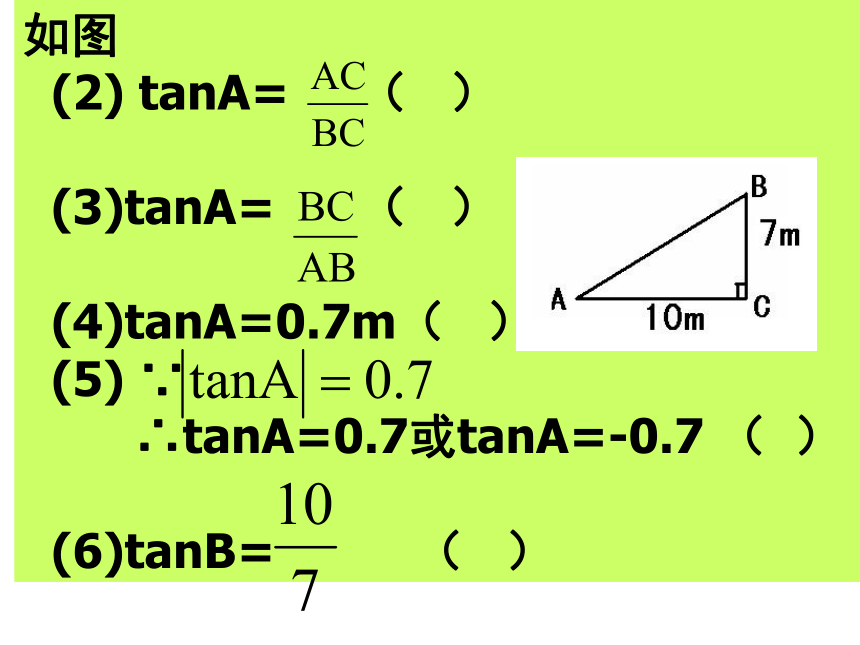
2、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )A、扩大100倍 B、缩小100倍 C、不变 D、不能确定3、已知∠A、∠B为锐角
(1) 若∠A=∠B,则tanA tanB
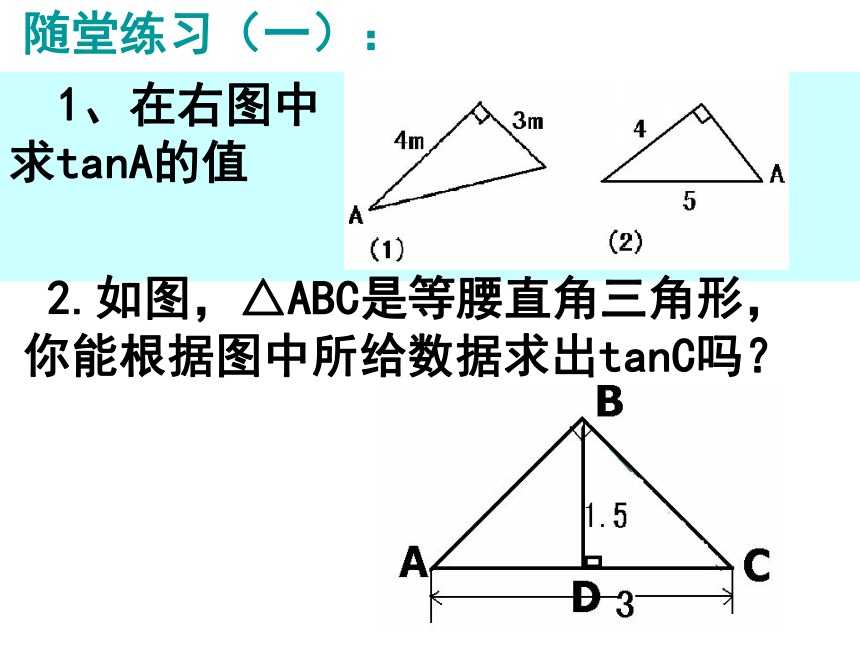
(2)若tanA=tanB,则∠A ∠B。 定义中应该注意的几个问题: 1、tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形) 2、tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”; 3、tanA是一个比值(直角边之比,注意比的顺序: );且tanA﹥0,无单位; 4、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。 5、角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等。 1、在右图中 求tanA的值
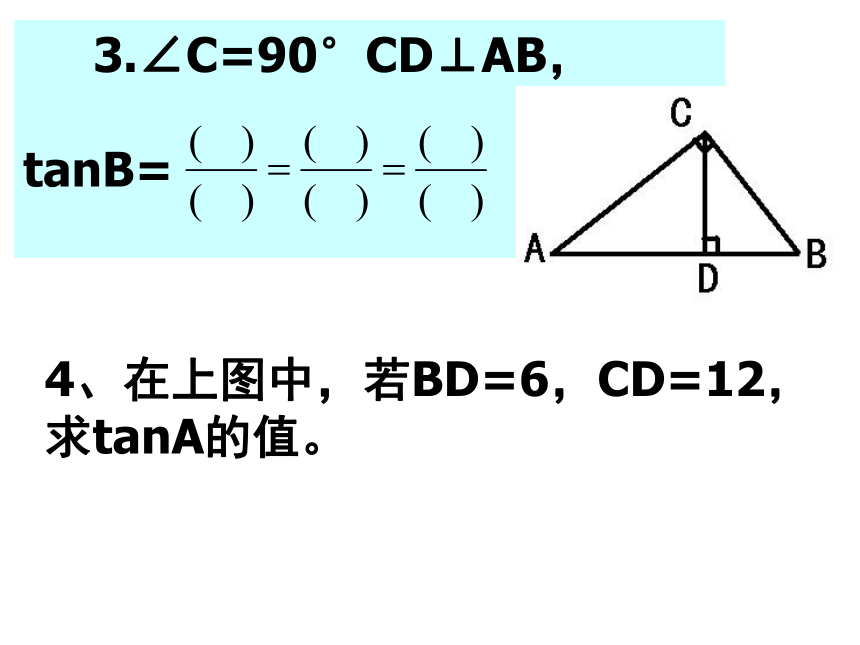
随堂练习(一): 2.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 3.∠C=90°CD⊥AB,
tanB=
4、在上图中,若BD=6,CD=12,求tanA的值。 例1:在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求tanA和tanB
(2)BC=3,tanA= ,求AC 和AB。
2、在等腰△ABC中,AB=AC=13,BC=10,求tanB。练习(二) 1、在Rt△ABC中,∠C=90°,
AB=15,tanA= ,求AC和BC。相信自己:(必做题)
1、在Rt△ABC中,∠C=90°, (1)AC=25,AB=27,求tanA和tanB
(2)BC=3,tanA=0.6,求AC 和AB。
(3)AC=4,tanA=0.8,求BC。
2、在梯形ABCD中,AD//BC,AB=DC=13,AD=8, BC=18,求tanB。挑战自己:(选做题) 1、在△ABC中,D是AB的中点,DC⊥AC,tan∠BCD=0.5,AB=4 ,求AC。1.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 2.如图,某人从山脚下的点A走了200m后到达山顶的点B.已知山顶B到山脚下的垂直距离是55m,求山坡的坡度(结果精确到0.001m).3.鉴宝专家—--是真是假:4.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定5.已知∠A,∠B为锐角
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.6.如图, ∠C=90°CD⊥AB.7.在上图中,若BD=6,CD=12.求tanA的值.8.如图,分别根据图(1)和图(2)求tanA的值.9.在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求tanA和tanB
(2)BC=3,tanA= ,求AC和AB.10.在Rt△ABC中,∠C=90°,AB=15,tanA= ,
求AC和BC.11.在等腰△ABC中,AB=AC=13,BC=10,
求tanB.提示:
过点A作AD垂直于BC于点D.
求锐角三角函数时,勾股定理的运用是很重要的.12. 在Rt△ABC中,∠C=90°.
(1)AC=25.AB=27.求tanA和tanB.
(2)BC=3,tanA=0.6,求AC 和AB.
(3)AC=4,tanA=0.8,求BC.13.在梯形ABCD中,AD//BC,AB=DC=13,AD=8,BC=18.
求:tanB.
如图, 1) tanA=
2、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )A、扩大100倍 B、缩小100倍 C、不变 D、不能确定3、已知∠A、∠B为锐角
(1) 若∠A=∠B,则tanA tanB
(2)若tanA=tanB,则∠A ∠B。 定义中应该注意的几个问题: 1、tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形) 2、tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”; 3、tanA是一个比值(直角边之比,注意比的顺序: );且tanA﹥0,无单位; 4、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。 5、角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等。 1、在右图中 求tanA的值
随堂练习(一): 2.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 3.∠C=90°CD⊥AB,
tanB=
4、在上图中,若BD=6,CD=12,求tanA的值。 例1:在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求tanA和tanB
(2)BC=3,tanA= ,求AC 和AB。
2、在等腰△ABC中,AB=AC=13,BC=10,求tanB。练习(二) 1、在Rt△ABC中,∠C=90°,
AB=15,tanA= ,求AC和BC。相信自己:(必做题)
1、在Rt△ABC中,∠C=90°, (1)AC=25,AB=27,求tanA和tanB
(2)BC=3,tanA=0.6,求AC 和AB。
(3)AC=4,tanA=0.8,求BC。
2、在梯形ABCD中,AD//BC,AB=DC=13,AD=8, BC=18,求tanB。挑战自己:(选做题) 1、在△ABC中,D是AB的中点,DC⊥AC,tan∠BCD=0.5,AB=4 ,求AC。1.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 2.如图,某人从山脚下的点A走了200m后到达山顶的点B.已知山顶B到山脚下的垂直距离是55m,求山坡的坡度(结果精确到0.001m).3.鉴宝专家—--是真是假:4.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定5.已知∠A,∠B为锐角
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.6.如图, ∠C=90°CD⊥AB.7.在上图中,若BD=6,CD=12.求tanA的值.8.如图,分别根据图(1)和图(2)求tanA的值.9.在Rt△ABC中,∠C=90°, (1)AC=3,AB=6,求tanA和tanB
(2)BC=3,tanA= ,求AC和AB.10.在Rt△ABC中,∠C=90°,AB=15,tanA= ,
求AC和BC.11.在等腰△ABC中,AB=AC=13,BC=10,
求tanB.提示:
过点A作AD垂直于BC于点D.
求锐角三角函数时,勾股定理的运用是很重要的.12. 在Rt△ABC中,∠C=90°.
(1)AC=25.AB=27.求tanA和tanB.
(2)BC=3,tanA=0.6,求AC 和AB.
(3)AC=4,tanA=0.8,求BC.13.在梯形ABCD中,AD//BC,AB=DC=13,AD=8,BC=18.
求:tanB.
