第九单元 数学广角:鸡兔同笼(教学课件)-四年级数学下册人教版(共37张PPT)
文档属性
| 名称 | 第九单元 数学广角:鸡兔同笼(教学课件)-四年级数学下册人教版(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-20 05:01:45 | ||
图片预览








文档简介
(共37张PPT)
数学广角——鸡兔同笼
小学数学·四年级(下)·RJ
感受古代数学问题的趣味性,提高学习数学的兴趣。
解“鸡兔同笼”问题的结构特点,会运用列表法、假设法解决问题,初步形成解决此类问题的一般性策略。
通过自主探索、合作交流,培养学生的合作意识和逻辑推理能力,体会解题策略的多样化,渗透化繁为简的思想。
自主探究解决问题的过程,会运用列表法、假设法解决“鸡兔同笼”问题。
运用不同的方法解决实际问题。
建立“鸡兔同笼”问题的数学模型,培养学生的模型思想。
红花头上戴,彩衣不用裁。
清早歌一曲,千门万户开。
(猜一动物)
2条腿
两只耳朵长又尖,短短尾巴翘后边。
爱吃萝卜爱吃菜,走起路来真可爱。
(猜一动物)
4条腿
猜谜语
那反过来如果有5个头,14只脚,该有几只鸡几只兔呢?
数字接龙游戏
一只鸡:
一个头,两只脚。
一只兔:
一个头,四只脚。
一只鸡和一只兔:
两个头,六只脚。
三只鸡和两只兔:
五个头,十四只脚。
我国古代数学名著《孙子算经》中记载了一道数学趣题——“鸡兔同笼”问题。
zhì
你知道这道题的意思吗?
笼子里有若干只鸡和兔。从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
此类问题因其计算同一个笼子中鸡和兔的只数而得名“鸡兔同笼”。
这类问题的基本特点是已知鸡和兔的总头数和总脚数,求鸡和兔各有几只。
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
你能解决这个问题吗?
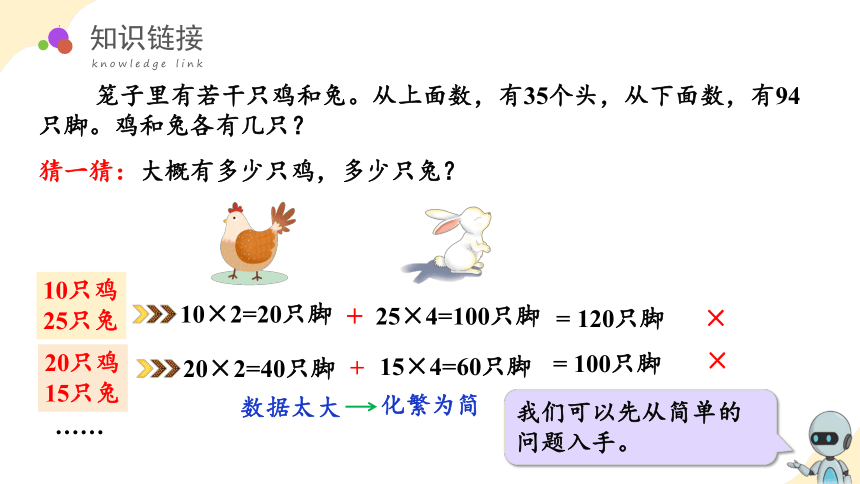
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
猜一猜:大概有多少只鸡,多少只兔?
化繁为简
数据太大
我们可以先从简单的问题入手。
25×4=100只脚
10×2=20只脚
10只鸡
25只兔
+
= 120只脚
×
15×4=60只脚
20×2=40只脚
+
= 100只脚
×
20只鸡
15只兔
……
探究鸡兔同笼解法
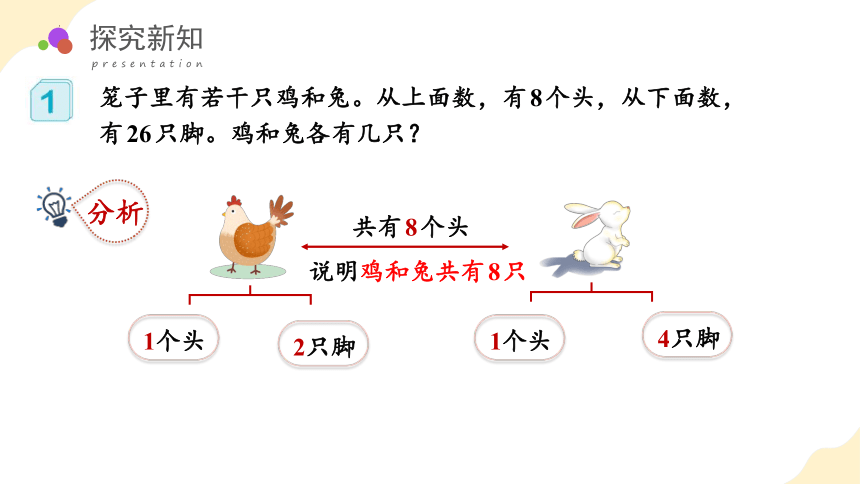
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
分析
1个头
2只脚
1个头
4只脚
共有8个头
说明鸡和兔共有8只
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
小组活动要求:
1.试一试:把你解决问题的过程记录下来;
2.说一说:与同桌交流你的方法;
3.想一想:答案正确吗?还有其他方法吗?
探究
不对,22只<26只,说明兔的只数猜少了
不对,24只<26只,说明兔的只数猜少了
猜对了
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
如果有3只兔,5只鸡,那么就有3×4+5×2=22(只)脚
如果有4只兔,4只鸡,那么就有4×4+4×2=24(只)脚
如果有5只兔,3只鸡,那么就有5×4+3×2=26(只)脚
方法一:猜测法
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法二:列表法
鸡
兔
脚
按照顺序列表试一试。
8
0
16
7
1
18
6
5
2
20
3
22
24
4
4
26
3
5
28
2
6
30
1
7
32
0
8
8
只
3
5
-1
-1
-1
-1
-1
+1
+1
+1
+1
+1
+2
+2
+2
+2
+2
鸡有3只,兔有5只。
将一只鸡换成一只兔,
则脚的数量增加2。
将一只兔换成一只鸡,
则脚的数量减少2。
①先画8个圆圈表示8只动物的头。
②再为每只动物画两只脚。
③把剩下的10只脚用完,要给其中的5只动物各添2只脚。
答:5只兔子,3只鸡。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法三:图示法
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法四:假设法
16
10
兔5只
鸡3只
思考:相差的10只脚是怎么产生的?
(1)假设笼子里都是鸡,共有 只脚。
笼子里实际有26只脚,相差 只脚。
8×2=16
26-16=10
每只鸡与每只兔相差 只脚。
4-2=2
用 表示头,用 表示脚。
给鸡添腿变兔子,兔有 只。
10÷2=5
8-5=3
鸡有 只。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法四:假设法
设鸡得兔法
兔的只数:
(26-8×2)÷(4-2)
=10÷2
=5(只)
鸡的只数:
8 – 5 = 3(只)
答:兔有5只,鸡有3只。
(1)假设笼子里全是鸡。
兔有 只。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法四:假设法
鸡3只
兔5只
思考:相差的6只脚是怎么产生的?
(2)假设笼子里都是兔,共有 只脚。
笼子里实际有26只脚,相差 只脚。
8×4=32
32-26=6
每只鸡与每只兔相差 只脚。
4-2=2
给兔子减腿变成鸡,鸡有 只。
6÷2=3
8-3=5
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法四:假设法
设兔得鸡法
鸡的只数:
(8×4-26)÷(4-2)
=6÷2
=3(只)
兔的只数:
8 - 3 = 5(只)
答:兔有5只,鸡有3只。
(2)假设笼子里全是兔。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法五:抬脚法
(1)假如让鸡和兔都抬起两只脚,一共抬起 8×2=16(只)脚。
(2)这时,剩下26 – 16 =10 (只)脚,全是兔子的脚。
(3)每只兔子还剩2只脚,所以兔子有10÷2=5(只),
鸡有8 – 5=3(只)。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法六:鸡翅膀加入法
(1)把鸡翅膀也看成两只脚,那么每只动物就都有4只脚。
共有8×4=32(只)脚。
(2)那么就多出来32 – 26 =6 (只)脚,多出来的是鸡的脚。
(3)所以有6÷2=3 (只)鸡,有8 – 3=5 (只)兔。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法七:兔子两个头法
(1)让兔子有两个头,那么一个头就对应两只脚,共有
26÷2=13 (个)头。
(2)那么就多出来13 – 8 =5(个)头,也就是兔子的数量。
(3)所以有8 – 5=3(只)鸡。
选择合适的方法,解决历史名题
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
兔:
(94 – 35×2)÷(4 – 2)
=24÷2
=12(只)
鸡:
35 – 12=23(只)
答:兔有12只,鸡有23只。
方法一:假设全是鸡
方法二:假设全是兔
鸡:
(35×4 – 94)÷(4 – 2)
=46÷2
=23(只)
兔:
35 – 23=12(只)
归纳小结
假设
计算
推理
解答
刚刚我们用了哪些方法解决了“鸡兔同笼”问题?
猜测法
列表法
图示法
假设法
抬脚法
鸡翅膀加入法
兔子两个头法
… …
猜测法和列表法效率低。对于数据较大的“鸡兔同笼”问题,一般用假设法来解决,也可以用“抬脚法”等其他方法来解决。
当用假设法解决“鸡兔同笼”问题时,假设全是鸡,先算出的是兔的只数;假设全是兔,先算出的是兔的只数。
想一想,说一说:在刚才“鸡兔同笼”计算过程中,有哪些注意事项?
鸡兔同笼真有趣,从古到今都研究。
读懂题意看数据,猜测、列表、假设来解决。
达标练习,巩固成果
1.
自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有多少辆
自行车:(10×3 26)÷(3 2)
=(30 26)÷1
=4÷1
=4(辆)
三轮车:10 4=6(辆)
答:自行车有4辆、三轮车有6辆。
假设全是三轮车
2.有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟、鹤各有几只?
假设全是鹤。
龟的只数:(112-40×2)÷(4-2)=16(只)
鹤的只数: 40-16=24(只)
答:龟有16只,鹤有24只。
日本的“龟鹤算” 问题就是从我国的“鸡兔同笼”问题演变来的。
3.一共有38人,租了8条船,每条船都坐满了。大、小船各租了几条?
大船限乘6人
小船限乘4人
假设全租小船。
大船:(38-8×4)÷(6-4)=3(条)
小船: 8-3=5(条)
答:大船租了3条,小船租了5条。
教材第101页“练习二十四”第3题
4. 篮球比赛中,3分线外投中一球记3分,3分线内投中一球记2分。在一场比赛中张鹏投了15个球,进了9个,没有罚球,总共得了21分。张鹏在这场比赛中投进了几个3分球
教材第101页“练习二十四”第5题
假设全是2分球。
(21-9×2)÷(3-2)=3(个)
答:张鹏在这场比赛中投进了3个3分球。
5. 花园路小学举办数学竞赛,试卷共有20道题,每做对一道题得5分,不做或做错一道题扣2分。壮壮共得79分,他做对了几道题?
假设所有的题全做对。
做错:(20×5-79)÷(5+2)=3(道)
做对:20-3=17(道)
答:他做对了17道题。
每一题对错相差5+2=7(分)
1个大和尚和3个小和尚一共吃了4个馒头。
每4个馒头正好分给1个大和尚和3个小和尚。
每4个馒头分为一组,一共可以分为:
100÷4=25(组),
而100个和尚正好分为25组。
在每组中,必有1个大和尚和3个小和尚。
组数:100÷(1+3)
=100÷4
=25(组)
答:大和尚有25人,小和尚有75人。
大和尚:25×1=25(人)
小和尚:25×3=75(人)
鸡兔同笼问题的解题方法
数据较大时,用假设法比较普遍,假设全部是某一种量,先求出的就是另一种量得数量。
还可以用抬腿法解决。
数据较小时,可以用猜想法、列表法解决。
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
数学广角——鸡兔同笼
小学数学·四年级(下)·RJ
感受古代数学问题的趣味性,提高学习数学的兴趣。
解“鸡兔同笼”问题的结构特点,会运用列表法、假设法解决问题,初步形成解决此类问题的一般性策略。
通过自主探索、合作交流,培养学生的合作意识和逻辑推理能力,体会解题策略的多样化,渗透化繁为简的思想。
自主探究解决问题的过程,会运用列表法、假设法解决“鸡兔同笼”问题。
运用不同的方法解决实际问题。
建立“鸡兔同笼”问题的数学模型,培养学生的模型思想。
红花头上戴,彩衣不用裁。
清早歌一曲,千门万户开。
(猜一动物)
2条腿
两只耳朵长又尖,短短尾巴翘后边。
爱吃萝卜爱吃菜,走起路来真可爱。
(猜一动物)
4条腿
猜谜语
那反过来如果有5个头,14只脚,该有几只鸡几只兔呢?
数字接龙游戏
一只鸡:
一个头,两只脚。
一只兔:
一个头,四只脚。
一只鸡和一只兔:
两个头,六只脚。
三只鸡和两只兔:
五个头,十四只脚。
我国古代数学名著《孙子算经》中记载了一道数学趣题——“鸡兔同笼”问题。
zhì
你知道这道题的意思吗?
笼子里有若干只鸡和兔。从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
此类问题因其计算同一个笼子中鸡和兔的只数而得名“鸡兔同笼”。
这类问题的基本特点是已知鸡和兔的总头数和总脚数,求鸡和兔各有几只。
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
你能解决这个问题吗?
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
猜一猜:大概有多少只鸡,多少只兔?
化繁为简
数据太大
我们可以先从简单的问题入手。
25×4=100只脚
10×2=20只脚
10只鸡
25只兔
+
= 120只脚
×
15×4=60只脚
20×2=40只脚
+
= 100只脚
×
20只鸡
15只兔
……
探究鸡兔同笼解法
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
分析
1个头
2只脚
1个头
4只脚
共有8个头
说明鸡和兔共有8只
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
小组活动要求:
1.试一试:把你解决问题的过程记录下来;
2.说一说:与同桌交流你的方法;
3.想一想:答案正确吗?还有其他方法吗?
探究
不对,22只<26只,说明兔的只数猜少了
不对,24只<26只,说明兔的只数猜少了
猜对了
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
如果有3只兔,5只鸡,那么就有3×4+5×2=22(只)脚
如果有4只兔,4只鸡,那么就有4×4+4×2=24(只)脚
如果有5只兔,3只鸡,那么就有5×4+3×2=26(只)脚
方法一:猜测法
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法二:列表法
鸡
兔
脚
按照顺序列表试一试。
8
0
16
7
1
18
6
5
2
20
3
22
24
4
4
26
3
5
28
2
6
30
1
7
32
0
8
8
只
3
5
-1
-1
-1
-1
-1
+1
+1
+1
+1
+1
+2
+2
+2
+2
+2
鸡有3只,兔有5只。
将一只鸡换成一只兔,
则脚的数量增加2。
将一只兔换成一只鸡,
则脚的数量减少2。
①先画8个圆圈表示8只动物的头。
②再为每只动物画两只脚。
③把剩下的10只脚用完,要给其中的5只动物各添2只脚。
答:5只兔子,3只鸡。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法三:图示法
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法四:假设法
16
10
兔5只
鸡3只
思考:相差的10只脚是怎么产生的?
(1)假设笼子里都是鸡,共有 只脚。
笼子里实际有26只脚,相差 只脚。
8×2=16
26-16=10
每只鸡与每只兔相差 只脚。
4-2=2
用 表示头,用 表示脚。
给鸡添腿变兔子,兔有 只。
10÷2=5
8-5=3
鸡有 只。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法四:假设法
设鸡得兔法
兔的只数:
(26-8×2)÷(4-2)
=10÷2
=5(只)
鸡的只数:
8 – 5 = 3(只)
答:兔有5只,鸡有3只。
(1)假设笼子里全是鸡。
兔有 只。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法四:假设法
鸡3只
兔5只
思考:相差的6只脚是怎么产生的?
(2)假设笼子里都是兔,共有 只脚。
笼子里实际有26只脚,相差 只脚。
8×4=32
32-26=6
每只鸡与每只兔相差 只脚。
4-2=2
给兔子减腿变成鸡,鸡有 只。
6÷2=3
8-3=5
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法四:假设法
设兔得鸡法
鸡的只数:
(8×4-26)÷(4-2)
=6÷2
=3(只)
兔的只数:
8 - 3 = 5(只)
答:兔有5只,鸡有3只。
(2)假设笼子里全是兔。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法五:抬脚法
(1)假如让鸡和兔都抬起两只脚,一共抬起 8×2=16(只)脚。
(2)这时,剩下26 – 16 =10 (只)脚,全是兔子的脚。
(3)每只兔子还剩2只脚,所以兔子有10÷2=5(只),
鸡有8 – 5=3(只)。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法六:鸡翅膀加入法
(1)把鸡翅膀也看成两只脚,那么每只动物就都有4只脚。
共有8×4=32(只)脚。
(2)那么就多出来32 – 26 =6 (只)脚,多出来的是鸡的脚。
(3)所以有6÷2=3 (只)鸡,有8 – 3=5 (只)兔。
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
方法七:兔子两个头法
(1)让兔子有两个头,那么一个头就对应两只脚,共有
26÷2=13 (个)头。
(2)那么就多出来13 – 8 =5(个)头,也就是兔子的数量。
(3)所以有8 – 5=3(只)鸡。
选择合适的方法,解决历史名题
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
兔:
(94 – 35×2)÷(4 – 2)
=24÷2
=12(只)
鸡:
35 – 12=23(只)
答:兔有12只,鸡有23只。
方法一:假设全是鸡
方法二:假设全是兔
鸡:
(35×4 – 94)÷(4 – 2)
=46÷2
=23(只)
兔:
35 – 23=12(只)
归纳小结
假设
计算
推理
解答
刚刚我们用了哪些方法解决了“鸡兔同笼”问题?
猜测法
列表法
图示法
假设法
抬脚法
鸡翅膀加入法
兔子两个头法
… …
猜测法和列表法效率低。对于数据较大的“鸡兔同笼”问题,一般用假设法来解决,也可以用“抬脚法”等其他方法来解决。
当用假设法解决“鸡兔同笼”问题时,假设全是鸡,先算出的是兔的只数;假设全是兔,先算出的是兔的只数。
想一想,说一说:在刚才“鸡兔同笼”计算过程中,有哪些注意事项?
鸡兔同笼真有趣,从古到今都研究。
读懂题意看数据,猜测、列表、假设来解决。
达标练习,巩固成果
1.
自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有多少辆
自行车:(10×3 26)÷(3 2)
=(30 26)÷1
=4÷1
=4(辆)
三轮车:10 4=6(辆)
答:自行车有4辆、三轮车有6辆。
假设全是三轮车
2.有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟、鹤各有几只?
假设全是鹤。
龟的只数:(112-40×2)÷(4-2)=16(只)
鹤的只数: 40-16=24(只)
答:龟有16只,鹤有24只。
日本的“龟鹤算” 问题就是从我国的“鸡兔同笼”问题演变来的。
3.一共有38人,租了8条船,每条船都坐满了。大、小船各租了几条?
大船限乘6人
小船限乘4人
假设全租小船。
大船:(38-8×4)÷(6-4)=3(条)
小船: 8-3=5(条)
答:大船租了3条,小船租了5条。
教材第101页“练习二十四”第3题
4. 篮球比赛中,3分线外投中一球记3分,3分线内投中一球记2分。在一场比赛中张鹏投了15个球,进了9个,没有罚球,总共得了21分。张鹏在这场比赛中投进了几个3分球
教材第101页“练习二十四”第5题
假设全是2分球。
(21-9×2)÷(3-2)=3(个)
答:张鹏在这场比赛中投进了3个3分球。
5. 花园路小学举办数学竞赛,试卷共有20道题,每做对一道题得5分,不做或做错一道题扣2分。壮壮共得79分,他做对了几道题?
假设所有的题全做对。
做错:(20×5-79)÷(5+2)=3(道)
做对:20-3=17(道)
答:他做对了17道题。
每一题对错相差5+2=7(分)
1个大和尚和3个小和尚一共吃了4个馒头。
每4个馒头正好分给1个大和尚和3个小和尚。
每4个馒头分为一组,一共可以分为:
100÷4=25(组),
而100个和尚正好分为25组。
在每组中,必有1个大和尚和3个小和尚。
组数:100÷(1+3)
=100÷4
=25(组)
答:大和尚有25人,小和尚有75人。
大和尚:25×1=25(人)
小和尚:25×3=75(人)
鸡兔同笼问题的解题方法
数据较大时,用假设法比较普遍,假设全部是某一种量,先求出的就是另一种量得数量。
还可以用抬腿法解决。
数据较小时,可以用猜想法、列表法解决。
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
