整式乘除[上学期]
图片预览






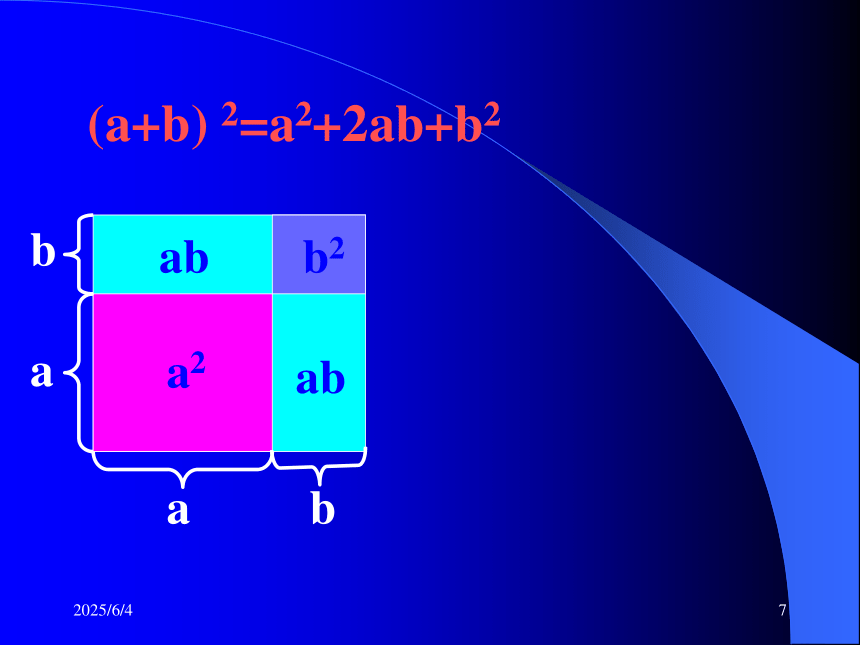
文档简介
课件16张PPT。整式的乘除——完全平方公式(1)2019-3-151教学过程复习提问
新课讲授
例题解析
课堂练习
课堂小结
课后作业2019-3-151(x+a)(x+b)= x2+(a+b)x+abⅠ.当a=-b时(x+a)(x+b)=x2-b2——平方差公式2019-3-1511。填空
( m + n )( m-n )= m2-n2
(2m-1)( 2m+1 ) = 4m2-1
(-2m+1)( 2m+1 ) = 1-4m2
2.计算: (a+2b+3)(a+2b-3)2019-3-151Ⅱ.当a=b时(x+a)(x+b)=?2019-3-151计算: (a+b)2 的值.解: (a+b)2= (a+b) (a+b)
=a2+ab+ab+b2
=a2+2ab+b2即: (a+b) 2=a2+2ab+b22019-3-151(a+b) 2=a2+2ab+b2baababa2b2ab2019-3-151问题:(a+b) 2 = a2 + b 2 ,对吗?为什么?答:不对。可以用特殊值的方法进行检验。
当a=2,b=1时,有
(a+b) 2 =9 ,
a2 + b 2 =5
所以 (a+b) 2 ≠ a2 + b 2 2019-3-151问题:你会用(a+b) 2=a2+2ab+b2 来计算(a-b) 2 吗?解: (a-b) 2 =﹝a+(﹣b) ﹞2
= a 2 + 2a﹙﹣b ﹚ + b 2
= a2 - 2ab+b22019-3-151完全平方公式(a+b) 2=a2+2ab+b2(a-b) 2=a2 - 2ab+b2 两数和(或差)的平方,等于它们
的平方和,加上(或者减去)它们的积
的2倍.2019-3-151例1.计算: (x+2y)2, (x-2y)2解: (x+2y)2=( a+ b)2=a2+2 a b+ b2=x2+4xy+4y2(x - 2y )2=(a - b )2 =a2 - 2 a b + b2x2 - 2· x· 2y +( 2y )2 x2+2·x·2y+(2y)2=x2 - 4xy+4y22019-3-151解:1) (4a-b)2 = (4a)2-2·4a·b+b2
= 16a2-8ab+b2 3) (-2x-1)2 =[-(2x+1)]2=(2x+1)2
= (2x)2+2·2x·1+1
=4x2+4x+12019-3-151例3.运用完全平方公式计算:
1) 1022 2) 1992解:1) 1022 = (100+2)2
= 1002+2×100×2+22
= 10000+400+4
= 10404
2)1992 = (200-1)2 =2002-2×200×1+12
= 40000-400+1
= 396012019-3-151小结:
1.完全平方公式是多项式乘法的特殊
情况,要熟记公式的左边和右边的
特点;
2.有时式子需要先进行变形,使变形
后的式子符合应用完全平方公式的
条件,即为“两数和(或差)”的平方,
然后应用公式计算.2019-3-151练习:
指出下列各式中的错误,并加以改正:
1) (-a-1)2 = -a2-2a-1;
2) (2a+1)2 =4a2+1;
3) (2a-1)2 =2a2 – 2a+1.2019-3-151作业:
教科书P133 习题7.7
A组 : 1
B组 : 1,3,4
新课讲授
例题解析
课堂练习
课堂小结
课后作业2019-3-151(x+a)(x+b)= x2+(a+b)x+abⅠ.当a=-b时(x+a)(x+b)=x2-b2——平方差公式2019-3-1511。填空
( m + n )( m-n )= m2-n2
(2m-1)( 2m+1 ) = 4m2-1
(-2m+1)( 2m+1 ) = 1-4m2
2.计算: (a+2b+3)(a+2b-3)2019-3-151Ⅱ.当a=b时(x+a)(x+b)=?2019-3-151计算: (a+b)2 的值.解: (a+b)2= (a+b) (a+b)
=a2+ab+ab+b2
=a2+2ab+b2即: (a+b) 2=a2+2ab+b22019-3-151(a+b) 2=a2+2ab+b2baababa2b2ab2019-3-151问题:(a+b) 2 = a2 + b 2 ,对吗?为什么?答:不对。可以用特殊值的方法进行检验。
当a=2,b=1时,有
(a+b) 2 =9 ,
a2 + b 2 =5
所以 (a+b) 2 ≠ a2 + b 2 2019-3-151问题:你会用(a+b) 2=a2+2ab+b2 来计算(a-b) 2 吗?解: (a-b) 2 =﹝a+(﹣b) ﹞2
= a 2 + 2a﹙﹣b ﹚ + b 2
= a2 - 2ab+b22019-3-151完全平方公式(a+b) 2=a2+2ab+b2(a-b) 2=a2 - 2ab+b2 两数和(或差)的平方,等于它们
的平方和,加上(或者减去)它们的积
的2倍.2019-3-151例1.计算: (x+2y)2, (x-2y)2解: (x+2y)2=( a+ b)2=a2+2 a b+ b2=x2+4xy+4y2(x - 2y )2=(a - b )2 =a2 - 2 a b + b2x2 - 2· x· 2y +( 2y )2 x2+2·x·2y+(2y)2=x2 - 4xy+4y22019-3-151解:1) (4a-b)2 = (4a)2-2·4a·b+b2
= 16a2-8ab+b2 3) (-2x-1)2 =[-(2x+1)]2=(2x+1)2
= (2x)2+2·2x·1+1
=4x2+4x+12019-3-151例3.运用完全平方公式计算:
1) 1022 2) 1992解:1) 1022 = (100+2)2
= 1002+2×100×2+22
= 10000+400+4
= 10404
2)1992 = (200-1)2 =2002-2×200×1+12
= 40000-400+1
= 396012019-3-151小结:
1.完全平方公式是多项式乘法的特殊
情况,要熟记公式的左边和右边的
特点;
2.有时式子需要先进行变形,使变形
后的式子符合应用完全平方公式的
条件,即为“两数和(或差)”的平方,
然后应用公式计算.2019-3-151练习:
指出下列各式中的错误,并加以改正:
1) (-a-1)2 = -a2-2a-1;
2) (2a+1)2 =4a2+1;
3) (2a-1)2 =2a2 – 2a+1.2019-3-151作业:
教科书P133 习题7.7
A组 : 1
B组 : 1,3,4
