幂的乘法与积的乘方[上学期]
文档属性
| 名称 | 幂的乘法与积的乘方[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-12-07 00:00:00 | ||
图片预览








文档简介
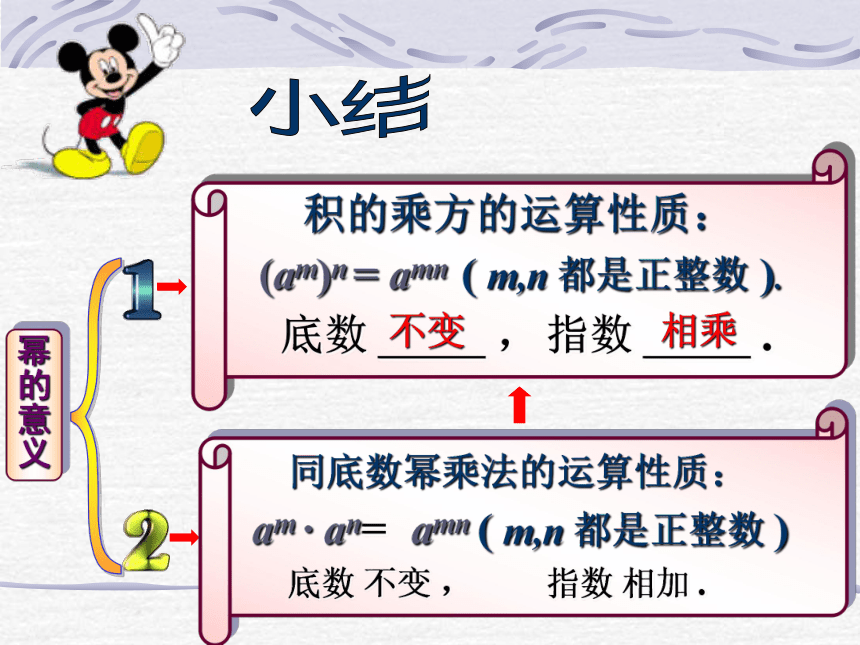
课件25张PPT。幂的乘方与积的乘方回顾与思考am · an= am+n?幂的意义:an=am+n(m,n都是正整数)做一做 根据乘方的意义及同底数幂的乘法计算下列各式,看看结果有什么规律?
(1) (62)4 ; (2) (a2)3 ; (3) (am)2 ; (4) (am)n .解:(1) (62)4 (2) (a2)3(3) (am)2= 62·62· 62·62=62+2+2+2=68= a2·a2·a2=a2+2+2=a6=am·am=am+m(4) (am)n=am·am· … ·am=am+m+ … +m=amn(幂的意义)(同底数幂的乘法性质)(乘法的意义)amnnn(am)n=amn (m,n都是正整数)底数 ,指数 . 幂的乘方,幂 的 乘 方 法则不变相乘例题解析例题解析 【例1】计算:
(1) (102)3 ; (2) (b5)5 ; (3) (an)3;
(4) -(x2)m ; (5) (y2)3 · y ; (6) 2(a2)6 - (a3)4 . (6) 2(a2)6 – (a3)4=102×3=106 ;(1) (102)3解:(2) (b5)5= b5×5= b25 ;(3) (an)3= an×3=a3n ;(4) -(x2)m= -x2×m= -x2m ;(5) (y2)3 · y= y2×3 · y= y6 · y=2a2×6 - a3×4=2a12-a12=a12.= y7;随堂练习p16 1、计算:
(1) (103)3 ; (2) -(a2)5 ; (3) (x3)4 · x2 ;
(4) [(-x)2 ]3 ; (5) (-a)2(a2)2; (6) x·x4 – x2 · x3 . 2. 判断下面计算是否正确?如果有错误请改正:
(1) (x3)3 = x6 ; (2)a6 · a4 = a24 .小结相乘不变思考下面两道题:(1)(2)我们只能根据乘方的意义及乘法交换律、结合律可以进行运算这两道题有什么特点?观察底数。底数为两个因式相乘,积的形式。我们学过的幂的运算性质适用吗?这种形式为积的乘方同理:根据上述方法计算下列各题:(乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则)积的乘方有什么规律呢?分组讨论积的乘方的运算性质:一般地:n个n个n个即: 积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.问题:能不能用积的乘方的性质计算?例2:计算分析:以上各题底数都含有两个或两个以上的因式,我们运用积的乘方的运算性质。同学们观察以下各题的底数 题型分析例1,计算:
(1)[(-a)3]3+(a4)2(-a)解原式=(-a)9+a8(-a)
=-a9-a9
=-2a9(2)(-x3)2(-y)2+(-x2)3(-y2)解原式=x6y2+(-x6)(-y2)
=x6y2+x6y2
=2x6y2(3)(a2b6)n+3(-ab3)2n+2(-anb3n)2解原式=a2nb6n+3(-a)2nb6n+2(-an)2b6n
=a2nb6n+3a2nb6n+2a2nb6n
=6a2nb6n练习计算:
(2an+1)32an-2+2an-2ana2-a2a3(-2an-1)4-an-1an+1-(a2)n例题2,把结果用科学计数法表示
(1)(-2×102)5
(2)(2×104)2×(5×103)2练习:3.2×(-104)×105×(5×104)2例3用简便方法计算(1) 48×0.258
解原式=(4×0.25)8
=18
=1(2)212×(-0.5)10解原式=210×22×(-0.5)10
=[2×(-0.5)]10×22
=4 练习:例4求下列式子中的正整数x(1)4x=2x+1
(2)3x+12x+1=62x-3解(1)(22)X=2X+122X=2x+12x=x+1
X=1例5。已知|x+y-3|+(x-y-1)2=0,求0.5[(-X2Y)2]3的值解:依题意得,x+y-3=0
x-y-1=0解得 x=2
y=10.5[(-x2y)2]3=0.5[(-X2)2y2]3=0.5x12y6
=0.5×212
=211例6比较大小355,444,533分析;要比较这三个数的大小必须使它们的底数相同或指数相同;355=(35)11=24311 444=(44)11=25611 533=(53)11=12511练习;比较2555,3444,4333你会吗?课堂练习1计算
(1)(54)6+(-5)13×58×53
(2) (34)3+(32)2××(32)3×9
2若(b2bx)2=(b4)3,则x=
3.求下列各式中的x
(1) 22x+3-22x+1=192
(1) (62)4 ; (2) (a2)3 ; (3) (am)2 ; (4) (am)n .解:(1) (62)4 (2) (a2)3(3) (am)2= 62·62· 62·62=62+2+2+2=68= a2·a2·a2=a2+2+2=a6=am·am=am+m(4) (am)n=am·am· … ·am=am+m+ … +m=amn(幂的意义)(同底数幂的乘法性质)(乘法的意义)amnnn(am)n=amn (m,n都是正整数)底数 ,指数 . 幂的乘方,幂 的 乘 方 法则不变相乘例题解析例题解析 【例1】计算:
(1) (102)3 ; (2) (b5)5 ; (3) (an)3;
(4) -(x2)m ; (5) (y2)3 · y ; (6) 2(a2)6 - (a3)4 . (6) 2(a2)6 – (a3)4=102×3=106 ;(1) (102)3解:(2) (b5)5= b5×5= b25 ;(3) (an)3= an×3=a3n ;(4) -(x2)m= -x2×m= -x2m ;(5) (y2)3 · y= y2×3 · y= y6 · y=2a2×6 - a3×4=2a12-a12=a12.= y7;随堂练习p16 1、计算:
(1) (103)3 ; (2) -(a2)5 ; (3) (x3)4 · x2 ;
(4) [(-x)2 ]3 ; (5) (-a)2(a2)2; (6) x·x4 – x2 · x3 . 2. 判断下面计算是否正确?如果有错误请改正:
(1) (x3)3 = x6 ; (2)a6 · a4 = a24 .小结相乘不变思考下面两道题:(1)(2)我们只能根据乘方的意义及乘法交换律、结合律可以进行运算这两道题有什么特点?观察底数。底数为两个因式相乘,积的形式。我们学过的幂的运算性质适用吗?这种形式为积的乘方同理:根据上述方法计算下列各题:(乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则)积的乘方有什么规律呢?分组讨论积的乘方的运算性质:一般地:n个n个n个即: 积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.问题:能不能用积的乘方的性质计算?例2:计算分析:以上各题底数都含有两个或两个以上的因式,我们运用积的乘方的运算性质。同学们观察以下各题的底数 题型分析例1,计算:
(1)[(-a)3]3+(a4)2(-a)解原式=(-a)9+a8(-a)
=-a9-a9
=-2a9(2)(-x3)2(-y)2+(-x2)3(-y2)解原式=x6y2+(-x6)(-y2)
=x6y2+x6y2
=2x6y2(3)(a2b6)n+3(-ab3)2n+2(-anb3n)2解原式=a2nb6n+3(-a)2nb6n+2(-an)2b6n
=a2nb6n+3a2nb6n+2a2nb6n
=6a2nb6n练习计算:
(2an+1)32an-2+2an-2ana2-a2a3(-2an-1)4-an-1an+1-(a2)n例题2,把结果用科学计数法表示
(1)(-2×102)5
(2)(2×104)2×(5×103)2练习:3.2×(-104)×105×(5×104)2例3用简便方法计算(1) 48×0.258
解原式=(4×0.25)8
=18
=1(2)212×(-0.5)10解原式=210×22×(-0.5)10
=[2×(-0.5)]10×22
=4 练习:例4求下列式子中的正整数x(1)4x=2x+1
(2)3x+12x+1=62x-3解(1)(22)X=2X+122X=2x+12x=x+1
X=1例5。已知|x+y-3|+(x-y-1)2=0,求0.5[(-X2Y)2]3的值解:依题意得,x+y-3=0
x-y-1=0解得 x=2
y=10.5[(-x2y)2]3=0.5[(-X2)2y2]3=0.5x12y6
=0.5×212
=211例6比较大小355,444,533分析;要比较这三个数的大小必须使它们的底数相同或指数相同;355=(35)11=24311 444=(44)11=25611 533=(53)11=12511练习;比较2555,3444,4333你会吗?课堂练习1计算
(1)(54)6+(-5)13×58×53
(2) (34)3+(32)2××(32)3×9
2若(b2bx)2=(b4)3,则x=
3.求下列各式中的x
(1) 22x+3-22x+1=192
