2022-2023学年人教版(五四制)七年级数学下册18.2三角形全等的判定达标测试题(含解析)
文档属性
| 名称 | 2022-2023学年人教版(五四制)七年级数学下册18.2三角形全等的判定达标测试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 383.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-20 21:29:11 | ||
图片预览



文档简介
2022-2023学年人教版(五四学制)七年级数学下册《18.2三角形全等的判定》
达标测试题(附答案)
一.选择题(共10小题,满分30分)
1.如图所示,已知点F、E分别在AB、AC上,且AE=AF,当满足下列条件仍无法确定的△ABE≌△ACF是( )
A.AB=AC B.CF=BE C.BF=CE D.∠B=∠C
2.根据下列条件能画出唯一△ABC的是( )
A.AB=2,BC=6,AC=9 B.AB=7,BC=5,∠A=30°
C.∠A=50°,∠B=60°,∠C=70° D.AC=3.5,BC=4.8,∠C=70°
3.一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中考虑最全面的是( )
A.带其中的任意两块去都可以
B.带1、2或2、3去就可以了
C.带1、4或3、4去就可以了
D.带1、4或2、3或3、4去均可
4.如图,在△ABC中,CD、BE分别是AB、AC边上的高,F是CD与BE的交点,若AD=FD,∠ABE=26°,则∠ACB的度数为( )
A.76° B.71° C.81° D.86°
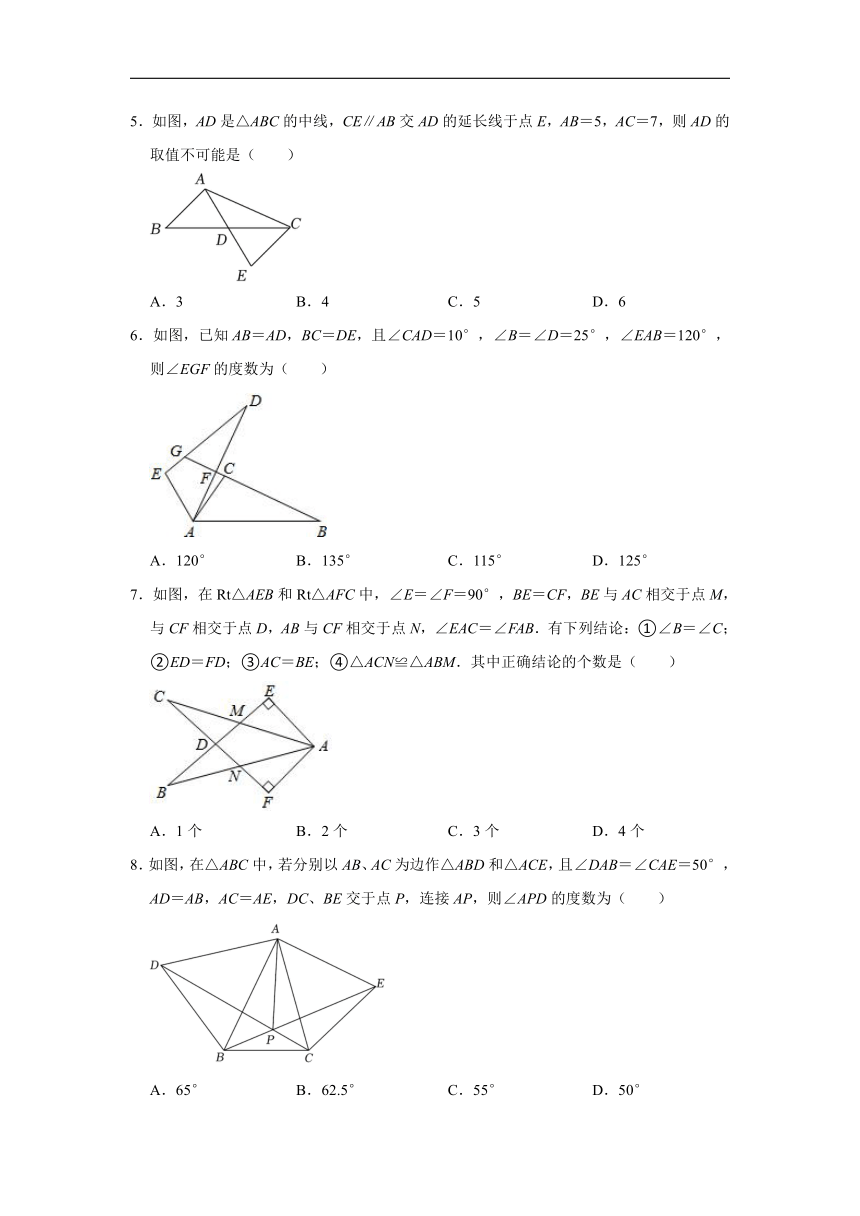
5.如图,AD是△ABC的中线,CE∥AB交AD的延长线于点E,AB=5,AC=7,则AD的取值不可能是( )
A.3 B.4 C.5 D.6
6.如图,已知AB=AD,BC=DE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,
则∠EGF的度数为( )
A.120° B.135° C.115° D.125°
7.如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE=CF,BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠EAC=∠FAB.有下列结论:①∠B=∠C;②ED=FD;③AC=BE;④△ACN≌△ABM.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
8.如图,在△ABC中,若分别以AB、AC为边作△ABD和△ACE,且∠DAB=∠CAE=50°,AD=AB,AC=AE,DC、BE交于点P,连接AP,则∠APD的度数为( )
A.65° B.62.5° C.55° D.50°
9.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的度数和为( )
A.60° B.75° C.90° D.120°
10.如图,CA⊥AB,垂足为点A,AB=12米,AC=6米,射线BM⊥AB,垂足为点B,动点E从A点出发以2米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过t秒时,由点D、E、B组成的三角形与△BCA全等.请问t有几种情况?( )
A.1种 B.2种 C.3种 D.4种
二.填空题(共9小题,满分36分)
11.如图,点B、A、D、E在同一直线上,BC=EF,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是 .(只填一个即可)
12.如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是 .
13.如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.
(1)若∠ECF=α,则∠CAB= (用含α的代数式表示);
(2)点E从点B出发,在直线BC上以每秒2cm的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动 s时,CF=AB.
14.如图,在△ABC和△AED中,AB=AC,AE=AD,∠BAC=∠EAD,且点E,A,B在同一直线上,点C,D在EB同侧,连结BD,CE交于点M.若∠CAD=100°,则∠DME= °.
15.如图,AB=AC,AD=AE,∠BAC=∠DAE,点B、D、E在同一条直线上,若∠1=25°,∠3=60°,则∠2的度数为 .
16.如图,△ABC的面积为15cm2,BP平分∠ABC,过点A作AP⊥BP于点P.则△PBC的面积为 cm2.
17.如图,在△ABC中,AB=AC,点D、E、F分别在边BC、AB、AC上,且CD=BE,BD=CF.若∠EDF=42°,则∠BAC的度数是 .
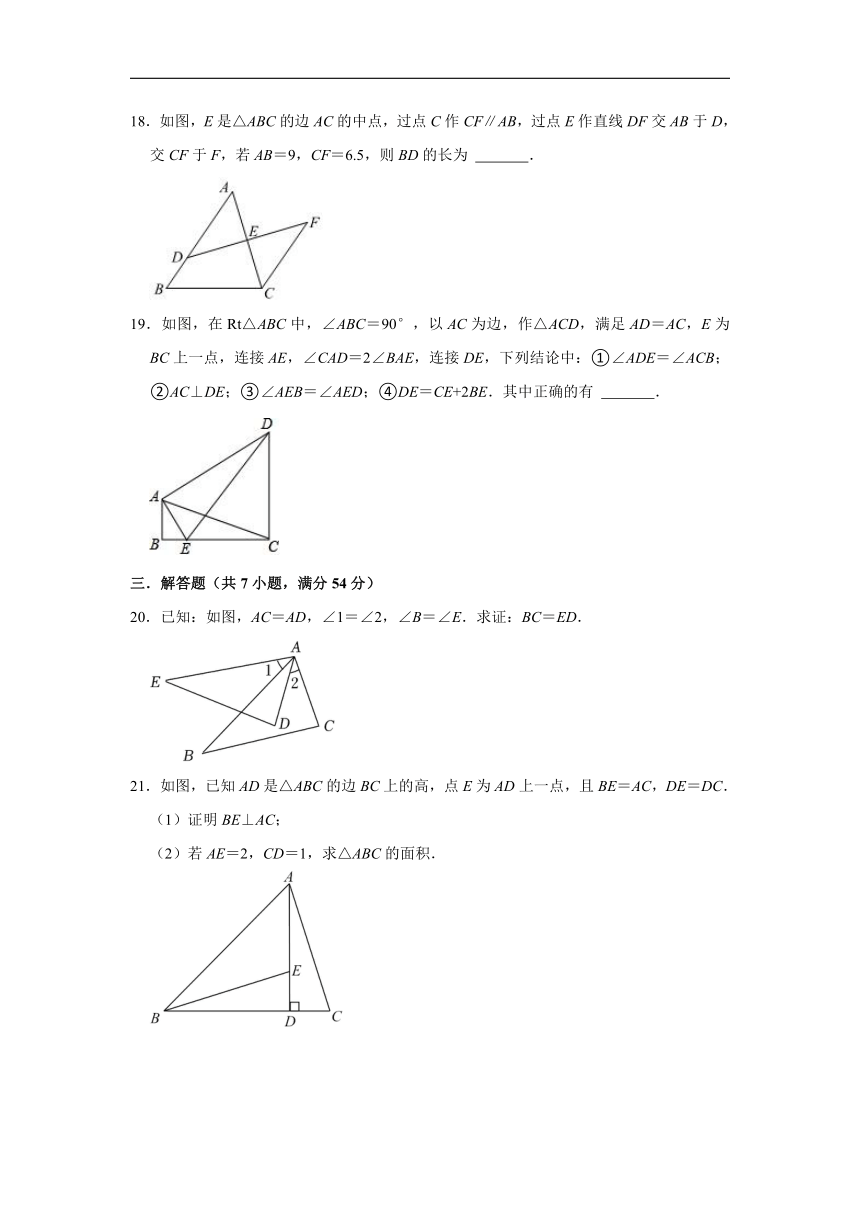
18.如图,E是△ABC的边AC的中点,过点C作CF∥AB,过点E作直线DF交AB于D,交CF于F,若AB=9,CF=6.5,则BD的长为 .
19.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,E为BC上一点,连接AE,∠CAD=2∠BAE,连接DE,下列结论中:①∠ADE=∠ACB;②AC⊥DE;③∠AEB=∠AED;④DE=CE+2BE.其中正确的有 .
三.解答题(共7小题,满分54分)
20.已知:如图,AC=AD,∠1=∠2,∠B=∠E.求证:BC=ED.
21.如图,已知AD是△ABC的边BC上的高,点E为AD上一点,且BE=AC,DE=DC.
(1)证明BE⊥AC;
(2)若AE=2,CD=1,求△ABC的面积.
22.如图,已知点C是AB的中点,CD∥BE,且CD=BE.
(1)求证:△ACD≌△CBE.
(2)若∠A=87°,∠D=32°,求∠B的度数.
23.用10块高度相同长方体小木块垒了两堵与地面垂直的木墙AD、BE,AD=9cm,BE=21cm,两木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.
24.如图,点A,B在射线CA,CB上,CA=CB.点E,F在射线CD上,∠BEC=∠CFA,∠BEC+∠BCA=180°.
(1)求证:△BCE≌△CAF;
(2)试判断线段EF,BE,AF的数量关系,并说明理由.
25.已知:如图,点A、E、F、C在同一条直线上,AD∥CB,∠1=∠2,AE=CF.
(1)求证:△ADF≌△CBE.
(2)若∠A=30°,∠CBF=20°,求∠DEF的度数.
26.如图,△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE.
(1)求证:BD=CE;
(2)若∠BAC=40°,求∠BMC的度数.
参考答案
一.选择题(共10小题,满分30分)
1.解:在△ABE和△ACD中,已知AE=AF,公共角∠BAE=∠CAF,
A、满足AB=AC,利用“SAS”证明△ABE≌△ACD,故A不符合题意;
B、满足CF=BE,不能证明△ABE≌△ACD,故B符合题意;
C、满足BF=CE,则AB=AC,利用“SAS”证明△ABE≌△ACD,故C不符合题意;
D、满足∠B=∠C,利用“AAS”可证明△ABE≌△ACD,故D不符合题意;
故选:B.
2.解:A、2+6=8<9,不满足三边关系,本选项不符合题意;
B、边边角三角形不能唯一确定.本选项不符合题意,
C、没有边的条件,三角形不能唯一确定,本选项不符合题意;
D、边角边,能确定唯一三角形.本选项符合题意.
故选:D.
3.解:带3、4可以用“角边角”确定三角形,
带1、4可以用“角边角”确定三角形,
故选:C.
4.解:∵CD、BE分别是AB、AC边上的高,
∴∠ADC=∠BDC=90°=∠AEB,
∴∠A+∠ACD=∠A+∠ABE,
∴∠ACD=∠ABE=26°,
在△ACD和△BFD中,
,
∴△ACD≌△BFD(AAS),
∴DC=DB,
∴∠DCB=∠DBC=45°,
∴∠ACB=∠ACD+∠DCB=45°+26°=71°,
故选:B.
5.解:∵AD 是△ABC 的中线,
∴CD=BD,
∵CE∥AB,
∴∠DCE=∠DBA,
在△CDE和△BDA中,
,
∴△CDE≌△BDA(SAS),
∴EC=AB=5,
∵7﹣5<AE<7+5,
∴2<2AD<12,
∴1<AD<6,
则AD的取值不可能是6.
故选:D.
6.解:∵AB=AD,BC=DE,∠B=∠D=25°,
∴△ABC≌△ADE(SAS),
∴∠DAE=∠CAB,
∵∠EAB=120°,∠CAD=10°,
∴∠EAD=∠CAB=55°,
∴∠DAB=65°,
∵∠GFD=∠AFB,∠B=∠D=25°,
∴∠DGB=∠DAB=65°,
∴∠EGF=115°.
故选:C.
7.解:∵∠EAC=∠FAB,
∴∠EAC+∠BAC=∠FAB+∠BAC,
即∠EAB=∠CAF,
在△ABE和△ACF,
,
∴△ABE≌△ACF(AAS),
∴∠B=∠C,AC=AB,AE=AF,
故①正确;
∵∠E=90°,
∴AB>BE,
∴AC>BE,
故③错误;
如图,连接AD,
在Rt△ADE和Rt△ADF中,
,
∴Rt△ADE≌Rt△ADF(HL),
∴∠DAE=∠DAF,
∵ED⊥AE,FD⊥AF,
∴ED=FD,
故②正确;
在△ACN和△ABM,
,
∴△ACN≌△ABM(ASA)(故④正确);
综上所述,正确的结论是①②④,共有3个.
故选:C.
8.解:如图,作AF⊥CD于点F,AG⊥BE于点G,则∠AFC=∠AGE=90°,
∵∠DAB=∠CAE=50°,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴∠ACF=∠AEG,
在△ACF和△AEG中
,
∴△ACF≌△AEG(AAS),
∴AF=AG,
∴点A在∠DPE的平分线上,
∴∠APE=∠APD=∠DPE,
∵∠CPE+∠ACF=∠CAE+∠AEG=∠AHP,
∴∠CPE=∠CAE=50°,
∴∠APD=∠APE=∠DPE=(180°﹣∠CPE)=65°,
故选:A.
9.解:∠ABC+∠DFE=90°,理由如下:
由题意可得:△ABC与△DEF均是直角三角形,且BC=EF,AC=DF.
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠ABC=∠DEF,
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°,
故选:C.
10.解:(1)当t=0时,ED=BC,AB=BA,Rt△ACB≌Rt△EBD;
(2)当t=3时,ED=BC,AC=EB,Rt△ACB≌Rt△EBD;
(3)当t=9时,ED=BC,AC=EB,Rt△ACB≌Rt△EBD;
(4)当t=12时,ED=BC,AB=EB,Rt△ACB≌Rt△EBD.
∴共有4种情况,
故选:D.
二.填空题(共9小题,满分36分)
11.解:∵BC∥EF,
∴∠B=∠E,
∵BC=EF,
若添加BA=ED,
∵BC∥EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);
若添加∠C=∠F,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
若添加∠BAC=∠EDF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS).
故答案为:BA=ED(或∠C=∠F或∠BAC=∠EDF).
12.解:由图得:遮挡住的三角形中露出两个角及其夹边.
∴根据三角形的判定方法ASA可解决此题.
故答案为:ASA.
13.解:(1)∵∠ACB=90°,
∴∠A+∠CBD=90°,
∵CD为AB边上的高,
∴∠CDB=90°,
∴∠BCD+∠CBD=90°,
∴∠A=∠BCD,
∵∠BCD=∠ECF,
∴∠ECF=∠A=α;
故答案为:α;
(2)∵过点E作BC的垂线交直线CD于点F,
∴∠CEF=90°=∠ACB,
在△CEF和△ACB中,
,
∴△CEF≌△ACB(AAS),
∴CE=AC=7cm,
①如图,当点E在射线BC上移动时,BE=CE+BC=7+3=10(cm),
∵点E从点B出发,在直线BC上以2cm的速度移动,
∴E移动了:10÷2=5(s);
②当点E在射线CB上移动时,CE′=AC﹣BC=7﹣3=4(cm),
∵点E从点B出发,在直线BC上以2cm的速度移动,
∴E移动了:4÷2=2(s);
综上所述,当点E在射线CB上移动5s或2s时,CF=AB;
故答案为:2或5.
14.解:∵∠BAC=∠EAD,
∴∠BAC+∠DAC=∠EAD+∠DAC,即∠DAB=∠EAC,
在△EAC和△DAB中,
,
∴△ABD≌△ACE(SAS),
∴∠ECA=∠DBA,
∵∠BAC=∠EAD,∠CAD=100°,
∴∠BAC=∠EAD=(180°﹣∠CAD)=40°,
∵∠BAC是△EAC的外角,
∴∠BAC=∠AEC+∠ACE=40°,
∵∠DME是△BME的外角,
∴∠DME=∠AEC+∠ABD=∠AEC+∠ACE=40°.
故答案为:40.
15.解:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠2=∠ABD,
∵∠1=25°,∠3=60°,
∴∠ABD=∠3﹣∠1=60°﹣25°=35°,
∴∠2=35°,
故答案为:35°.
16.解:延长AP交BC于E,
∵BP平分∠ABC,
∴∠ABP=∠EBP,
∵AP⊥BP,
∴∠APB=∠EPB=90°,
在△ABP和△EBP中,
,
∴△ABP≌△EBP(ASA),
∴AP=PE,
∴S△ABP=S△EBP,S△ACP=S△ECP,
∴S△PBC=S△ABC=×15=7.5(cm2),
故答案为:7.5.
17.解:∵AB=AC,
∴∠B=∠C,
在△BDE与△CFD中,
,
∴△BDE≌△CFD(SAS),
∴∠EDB=∠DFC,∠FDC=∠BED,
∵∠EDF+∠BDE+∠FDC=180°,
∵∠B+∠BED+∠EDB=180°,
∴∠B=∠EDF=42°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣42°﹣42°=96°,
故答案为:96°.
18.证明:∵CF∥AB,
∴∠ADE=∠F,∠FCE=∠A,
∵点E为AC的中点,
∴AE=EC,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS),
∴AD=CF=6.5,
∵AB=9,
∴BD=AB﹣AD=9﹣6.5=2.5,
故答案为:2.5.
19.解:如图,设AC交DE于点G,延长CB到点F,使BF=BE,连接AF,
∵∠ABC=90°,
∴AB垂直平分EF,
∴AE=AF,
∴∠EAB=∠FAB,
∵∠CAD=2∠BAE,∠FAE=2∠BAE,
∴∠CAD=∠FAE,
∴∠CAD+∠CAE=∠FAE+∠CAE,
∴∠EAD=∠FAC,
在△EAD和△FAC中,
,
∴△EAD≌△FAC(SAS),
∴∠ADE=∠ACB,
故①正确;
假设AC⊥DE成立,则∠AGE=90°,
∴∠EAG=90°﹣∠AED=∠ADE=∠ACB,
∴AE=CE,
∴DE垂直平分AC,
∴AD=CD,
∴△ACD是等边三角形,
∴∠FAE=∠CAD=60°,
∴∠BAE=30°,
∴∠AEB=60°,
∴∠EAG=∠ACB=30°,
∴∠BAC=60°,
显然,与题中所给条件不符,
故②错误;
∵∠AEB=∠F,∠F=∠AED,
∴∠AEB=∠AED,
故③正确;
∵FE=2BE,
∴DE=CF=CE+FE=CE+2BE,
故④正确,
故答案为:①③④.
三.解答题(共7小题,满分54分)
20.证明:∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,
∴∠EAD=∠BAC,
在△ABC和△AED中,
,
∴△ABC≌△AED(AAS),
∴BC=ED.
21.(1)证明:延长BE交AC于点F,
∵AD为△ABC边BC上的高.
∴AD⊥BC,
∴∠BDE=∠ADC=90°,
在Rt△BDE和Rt△ADC 中,
,
∴Rt△BDE≌Rt△ADC(HL),
∴∠DBE=∠DAC,
在△BDE中,∠BDE=90°,
∴∠DBE+∠BED=90°,
∴∠DAC+∠BED=90°,
∵∠AEF=∠BED,
∴∠AEF+∠DAC=90°,
∴∠AFE=180°﹣(∠DAC﹣∠AEF)=90°,
∴BE⊥AC;
(2)解:∵△BDE≌△ADC,
∴CD=DE=1,BD=AD,
∵AE=2,
∴AD=AE+DE=2+1=3,
∴BC=BD+CD=3+1=4,
∴S△ABC=BC AD=×4×3=6.
22.(1)证明:∵C是AB的中点(已知),
∴AC=CB(线段中点的定义).
∵CD∥BE(已知),
∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS).
(2)解:∵△ACD≌△CBE,∠A=87°,∠D=32°,
∴∠B=∠ACD,
∴∠ACD=180°﹣∠A﹣∠D
=180°﹣87°﹣32°
=61,
∵∠B=61°.
23.解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=9cm,DC=BE=21cm,
∴DE=DC+CE=30(cm),
答:两堵木墙之间的距离为30cm.
24.(1)证明:∵∠BEC+∠BCA=180°,
∴∠BEC+∠ECB+∠ACF=180°,
∵∠CFA+∠ACF+∠FAC=180°,∠BEC=∠CFA,
∴∠BCF=∠FAC,
在△BCE与△CAF中
,
∴△BCE≌△CAF(AAS);
(2)解:AF+EF=BE,理由如下:
∵△BCE≌△CAF,
∴AF=CE,CF=BE,
∵CE+EF=CF,
∴AF+EF=BE.
25.(1)证明:∵AD∥CB,
∴∠A=∠C,
∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
在△ADF和△CBE中,
,
∴△ADF≌△CBE(ASA).
(2)由(1)得DF=BE,
在△DFE和△BEF中,
,
∴△DFE≌△BEF(SAS),
∵∠A=∠C=30°,∠CBF=20°,
∴∠BFE=∠C+∠CBF=50°,
∴∠DEF=∠BFE=50°,
∴∠DEF的度数是50°.
26.(1)证明:∵∠BAC=∠DAE,
∴∠BAC+∠DAC=∠DAE+∠DAC.
即∠BAD=∠CAE.
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS).
∴BD=CE.
(2)解:设AC与BD交于点N,
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ANB=∠CNM,
∴∠BMC=∠BAC=40°.
达标测试题(附答案)
一.选择题(共10小题,满分30分)
1.如图所示,已知点F、E分别在AB、AC上,且AE=AF,当满足下列条件仍无法确定的△ABE≌△ACF是( )
A.AB=AC B.CF=BE C.BF=CE D.∠B=∠C
2.根据下列条件能画出唯一△ABC的是( )
A.AB=2,BC=6,AC=9 B.AB=7,BC=5,∠A=30°
C.∠A=50°,∠B=60°,∠C=70° D.AC=3.5,BC=4.8,∠C=70°
3.一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中考虑最全面的是( )
A.带其中的任意两块去都可以
B.带1、2或2、3去就可以了
C.带1、4或3、4去就可以了
D.带1、4或2、3或3、4去均可
4.如图,在△ABC中,CD、BE分别是AB、AC边上的高,F是CD与BE的交点,若AD=FD,∠ABE=26°,则∠ACB的度数为( )
A.76° B.71° C.81° D.86°
5.如图,AD是△ABC的中线,CE∥AB交AD的延长线于点E,AB=5,AC=7,则AD的取值不可能是( )
A.3 B.4 C.5 D.6
6.如图,已知AB=AD,BC=DE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,
则∠EGF的度数为( )
A.120° B.135° C.115° D.125°
7.如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE=CF,BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠EAC=∠FAB.有下列结论:①∠B=∠C;②ED=FD;③AC=BE;④△ACN≌△ABM.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
8.如图,在△ABC中,若分别以AB、AC为边作△ABD和△ACE,且∠DAB=∠CAE=50°,AD=AB,AC=AE,DC、BE交于点P,连接AP,则∠APD的度数为( )
A.65° B.62.5° C.55° D.50°
9.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的度数和为( )
A.60° B.75° C.90° D.120°
10.如图,CA⊥AB,垂足为点A,AB=12米,AC=6米,射线BM⊥AB,垂足为点B,动点E从A点出发以2米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过t秒时,由点D、E、B组成的三角形与△BCA全等.请问t有几种情况?( )
A.1种 B.2种 C.3种 D.4种
二.填空题(共9小题,满分36分)
11.如图,点B、A、D、E在同一直线上,BC=EF,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是 .(只填一个即可)
12.如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是 .
13.如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.
(1)若∠ECF=α,则∠CAB= (用含α的代数式表示);
(2)点E从点B出发,在直线BC上以每秒2cm的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动 s时,CF=AB.
14.如图,在△ABC和△AED中,AB=AC,AE=AD,∠BAC=∠EAD,且点E,A,B在同一直线上,点C,D在EB同侧,连结BD,CE交于点M.若∠CAD=100°,则∠DME= °.
15.如图,AB=AC,AD=AE,∠BAC=∠DAE,点B、D、E在同一条直线上,若∠1=25°,∠3=60°,则∠2的度数为 .
16.如图,△ABC的面积为15cm2,BP平分∠ABC,过点A作AP⊥BP于点P.则△PBC的面积为 cm2.
17.如图,在△ABC中,AB=AC,点D、E、F分别在边BC、AB、AC上,且CD=BE,BD=CF.若∠EDF=42°,则∠BAC的度数是 .
18.如图,E是△ABC的边AC的中点,过点C作CF∥AB,过点E作直线DF交AB于D,交CF于F,若AB=9,CF=6.5,则BD的长为 .
19.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,E为BC上一点,连接AE,∠CAD=2∠BAE,连接DE,下列结论中:①∠ADE=∠ACB;②AC⊥DE;③∠AEB=∠AED;④DE=CE+2BE.其中正确的有 .
三.解答题(共7小题,满分54分)
20.已知:如图,AC=AD,∠1=∠2,∠B=∠E.求证:BC=ED.
21.如图,已知AD是△ABC的边BC上的高,点E为AD上一点,且BE=AC,DE=DC.
(1)证明BE⊥AC;
(2)若AE=2,CD=1,求△ABC的面积.
22.如图,已知点C是AB的中点,CD∥BE,且CD=BE.
(1)求证:△ACD≌△CBE.
(2)若∠A=87°,∠D=32°,求∠B的度数.
23.用10块高度相同长方体小木块垒了两堵与地面垂直的木墙AD、BE,AD=9cm,BE=21cm,两木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.
24.如图,点A,B在射线CA,CB上,CA=CB.点E,F在射线CD上,∠BEC=∠CFA,∠BEC+∠BCA=180°.
(1)求证:△BCE≌△CAF;
(2)试判断线段EF,BE,AF的数量关系,并说明理由.
25.已知:如图,点A、E、F、C在同一条直线上,AD∥CB,∠1=∠2,AE=CF.
(1)求证:△ADF≌△CBE.
(2)若∠A=30°,∠CBF=20°,求∠DEF的度数.
26.如图,△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE.
(1)求证:BD=CE;
(2)若∠BAC=40°,求∠BMC的度数.
参考答案
一.选择题(共10小题,满分30分)
1.解:在△ABE和△ACD中,已知AE=AF,公共角∠BAE=∠CAF,
A、满足AB=AC,利用“SAS”证明△ABE≌△ACD,故A不符合题意;
B、满足CF=BE,不能证明△ABE≌△ACD,故B符合题意;
C、满足BF=CE,则AB=AC,利用“SAS”证明△ABE≌△ACD,故C不符合题意;
D、满足∠B=∠C,利用“AAS”可证明△ABE≌△ACD,故D不符合题意;
故选:B.
2.解:A、2+6=8<9,不满足三边关系,本选项不符合题意;
B、边边角三角形不能唯一确定.本选项不符合题意,
C、没有边的条件,三角形不能唯一确定,本选项不符合题意;
D、边角边,能确定唯一三角形.本选项符合题意.
故选:D.
3.解:带3、4可以用“角边角”确定三角形,
带1、4可以用“角边角”确定三角形,
故选:C.
4.解:∵CD、BE分别是AB、AC边上的高,
∴∠ADC=∠BDC=90°=∠AEB,
∴∠A+∠ACD=∠A+∠ABE,
∴∠ACD=∠ABE=26°,
在△ACD和△BFD中,
,
∴△ACD≌△BFD(AAS),
∴DC=DB,
∴∠DCB=∠DBC=45°,
∴∠ACB=∠ACD+∠DCB=45°+26°=71°,
故选:B.
5.解:∵AD 是△ABC 的中线,
∴CD=BD,
∵CE∥AB,
∴∠DCE=∠DBA,
在△CDE和△BDA中,
,
∴△CDE≌△BDA(SAS),
∴EC=AB=5,
∵7﹣5<AE<7+5,
∴2<2AD<12,
∴1<AD<6,
则AD的取值不可能是6.
故选:D.
6.解:∵AB=AD,BC=DE,∠B=∠D=25°,
∴△ABC≌△ADE(SAS),
∴∠DAE=∠CAB,
∵∠EAB=120°,∠CAD=10°,
∴∠EAD=∠CAB=55°,
∴∠DAB=65°,
∵∠GFD=∠AFB,∠B=∠D=25°,
∴∠DGB=∠DAB=65°,
∴∠EGF=115°.
故选:C.
7.解:∵∠EAC=∠FAB,
∴∠EAC+∠BAC=∠FAB+∠BAC,
即∠EAB=∠CAF,
在△ABE和△ACF,
,
∴△ABE≌△ACF(AAS),
∴∠B=∠C,AC=AB,AE=AF,
故①正确;
∵∠E=90°,
∴AB>BE,
∴AC>BE,
故③错误;
如图,连接AD,
在Rt△ADE和Rt△ADF中,
,
∴Rt△ADE≌Rt△ADF(HL),
∴∠DAE=∠DAF,
∵ED⊥AE,FD⊥AF,
∴ED=FD,
故②正确;
在△ACN和△ABM,
,
∴△ACN≌△ABM(ASA)(故④正确);
综上所述,正确的结论是①②④,共有3个.
故选:C.
8.解:如图,作AF⊥CD于点F,AG⊥BE于点G,则∠AFC=∠AGE=90°,
∵∠DAB=∠CAE=50°,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴∠ACF=∠AEG,
在△ACF和△AEG中
,
∴△ACF≌△AEG(AAS),
∴AF=AG,
∴点A在∠DPE的平分线上,
∴∠APE=∠APD=∠DPE,
∵∠CPE+∠ACF=∠CAE+∠AEG=∠AHP,
∴∠CPE=∠CAE=50°,
∴∠APD=∠APE=∠DPE=(180°﹣∠CPE)=65°,
故选:A.
9.解:∠ABC+∠DFE=90°,理由如下:
由题意可得:△ABC与△DEF均是直角三角形,且BC=EF,AC=DF.
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠ABC=∠DEF,
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°,
故选:C.
10.解:(1)当t=0时,ED=BC,AB=BA,Rt△ACB≌Rt△EBD;
(2)当t=3时,ED=BC,AC=EB,Rt△ACB≌Rt△EBD;
(3)当t=9时,ED=BC,AC=EB,Rt△ACB≌Rt△EBD;
(4)当t=12时,ED=BC,AB=EB,Rt△ACB≌Rt△EBD.
∴共有4种情况,
故选:D.
二.填空题(共9小题,满分36分)
11.解:∵BC∥EF,
∴∠B=∠E,
∵BC=EF,
若添加BA=ED,
∵BC∥EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS);
若添加∠C=∠F,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
若添加∠BAC=∠EDF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS).
故答案为:BA=ED(或∠C=∠F或∠BAC=∠EDF).
12.解:由图得:遮挡住的三角形中露出两个角及其夹边.
∴根据三角形的判定方法ASA可解决此题.
故答案为:ASA.
13.解:(1)∵∠ACB=90°,
∴∠A+∠CBD=90°,
∵CD为AB边上的高,
∴∠CDB=90°,
∴∠BCD+∠CBD=90°,
∴∠A=∠BCD,
∵∠BCD=∠ECF,
∴∠ECF=∠A=α;
故答案为:α;
(2)∵过点E作BC的垂线交直线CD于点F,
∴∠CEF=90°=∠ACB,
在△CEF和△ACB中,
,
∴△CEF≌△ACB(AAS),
∴CE=AC=7cm,
①如图,当点E在射线BC上移动时,BE=CE+BC=7+3=10(cm),
∵点E从点B出发,在直线BC上以2cm的速度移动,
∴E移动了:10÷2=5(s);
②当点E在射线CB上移动时,CE′=AC﹣BC=7﹣3=4(cm),
∵点E从点B出发,在直线BC上以2cm的速度移动,
∴E移动了:4÷2=2(s);
综上所述,当点E在射线CB上移动5s或2s时,CF=AB;
故答案为:2或5.
14.解:∵∠BAC=∠EAD,
∴∠BAC+∠DAC=∠EAD+∠DAC,即∠DAB=∠EAC,
在△EAC和△DAB中,
,
∴△ABD≌△ACE(SAS),
∴∠ECA=∠DBA,
∵∠BAC=∠EAD,∠CAD=100°,
∴∠BAC=∠EAD=(180°﹣∠CAD)=40°,
∵∠BAC是△EAC的外角,
∴∠BAC=∠AEC+∠ACE=40°,
∵∠DME是△BME的外角,
∴∠DME=∠AEC+∠ABD=∠AEC+∠ACE=40°.
故答案为:40.
15.解:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠2=∠ABD,
∵∠1=25°,∠3=60°,
∴∠ABD=∠3﹣∠1=60°﹣25°=35°,
∴∠2=35°,
故答案为:35°.
16.解:延长AP交BC于E,
∵BP平分∠ABC,
∴∠ABP=∠EBP,
∵AP⊥BP,
∴∠APB=∠EPB=90°,
在△ABP和△EBP中,
,
∴△ABP≌△EBP(ASA),
∴AP=PE,
∴S△ABP=S△EBP,S△ACP=S△ECP,
∴S△PBC=S△ABC=×15=7.5(cm2),
故答案为:7.5.
17.解:∵AB=AC,
∴∠B=∠C,
在△BDE与△CFD中,
,
∴△BDE≌△CFD(SAS),
∴∠EDB=∠DFC,∠FDC=∠BED,
∵∠EDF+∠BDE+∠FDC=180°,
∵∠B+∠BED+∠EDB=180°,
∴∠B=∠EDF=42°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣42°﹣42°=96°,
故答案为:96°.
18.证明:∵CF∥AB,
∴∠ADE=∠F,∠FCE=∠A,
∵点E为AC的中点,
∴AE=EC,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS),
∴AD=CF=6.5,
∵AB=9,
∴BD=AB﹣AD=9﹣6.5=2.5,
故答案为:2.5.
19.解:如图,设AC交DE于点G,延长CB到点F,使BF=BE,连接AF,
∵∠ABC=90°,
∴AB垂直平分EF,
∴AE=AF,
∴∠EAB=∠FAB,
∵∠CAD=2∠BAE,∠FAE=2∠BAE,
∴∠CAD=∠FAE,
∴∠CAD+∠CAE=∠FAE+∠CAE,
∴∠EAD=∠FAC,
在△EAD和△FAC中,
,
∴△EAD≌△FAC(SAS),
∴∠ADE=∠ACB,
故①正确;
假设AC⊥DE成立,则∠AGE=90°,
∴∠EAG=90°﹣∠AED=∠ADE=∠ACB,
∴AE=CE,
∴DE垂直平分AC,
∴AD=CD,
∴△ACD是等边三角形,
∴∠FAE=∠CAD=60°,
∴∠BAE=30°,
∴∠AEB=60°,
∴∠EAG=∠ACB=30°,
∴∠BAC=60°,
显然,与题中所给条件不符,
故②错误;
∵∠AEB=∠F,∠F=∠AED,
∴∠AEB=∠AED,
故③正确;
∵FE=2BE,
∴DE=CF=CE+FE=CE+2BE,
故④正确,
故答案为:①③④.
三.解答题(共7小题,满分54分)
20.证明:∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,
∴∠EAD=∠BAC,
在△ABC和△AED中,
,
∴△ABC≌△AED(AAS),
∴BC=ED.
21.(1)证明:延长BE交AC于点F,
∵AD为△ABC边BC上的高.
∴AD⊥BC,
∴∠BDE=∠ADC=90°,
在Rt△BDE和Rt△ADC 中,
,
∴Rt△BDE≌Rt△ADC(HL),
∴∠DBE=∠DAC,
在△BDE中,∠BDE=90°,
∴∠DBE+∠BED=90°,
∴∠DAC+∠BED=90°,
∵∠AEF=∠BED,
∴∠AEF+∠DAC=90°,
∴∠AFE=180°﹣(∠DAC﹣∠AEF)=90°,
∴BE⊥AC;
(2)解:∵△BDE≌△ADC,
∴CD=DE=1,BD=AD,
∵AE=2,
∴AD=AE+DE=2+1=3,
∴BC=BD+CD=3+1=4,
∴S△ABC=BC AD=×4×3=6.
22.(1)证明:∵C是AB的中点(已知),
∴AC=CB(线段中点的定义).
∵CD∥BE(已知),
∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS).
(2)解:∵△ACD≌△CBE,∠A=87°,∠D=32°,
∴∠B=∠ACD,
∴∠ACD=180°﹣∠A﹣∠D
=180°﹣87°﹣32°
=61,
∵∠B=61°.
23.解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=9cm,DC=BE=21cm,
∴DE=DC+CE=30(cm),
答:两堵木墙之间的距离为30cm.
24.(1)证明:∵∠BEC+∠BCA=180°,
∴∠BEC+∠ECB+∠ACF=180°,
∵∠CFA+∠ACF+∠FAC=180°,∠BEC=∠CFA,
∴∠BCF=∠FAC,
在△BCE与△CAF中
,
∴△BCE≌△CAF(AAS);
(2)解:AF+EF=BE,理由如下:
∵△BCE≌△CAF,
∴AF=CE,CF=BE,
∵CE+EF=CF,
∴AF+EF=BE.
25.(1)证明:∵AD∥CB,
∴∠A=∠C,
∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
在△ADF和△CBE中,
,
∴△ADF≌△CBE(ASA).
(2)由(1)得DF=BE,
在△DFE和△BEF中,
,
∴△DFE≌△BEF(SAS),
∵∠A=∠C=30°,∠CBF=20°,
∴∠BFE=∠C+∠CBF=50°,
∴∠DEF=∠BFE=50°,
∴∠DEF的度数是50°.
26.(1)证明:∵∠BAC=∠DAE,
∴∠BAC+∠DAC=∠DAE+∠DAC.
即∠BAD=∠CAE.
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS).
∴BD=CE.
(2)解:设AC与BD交于点N,
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ANB=∠CNM,
∴∠BMC=∠BAC=40°.
