18.1 勾股定理 课件(共46张PPT) 初中数学沪科版八年级下册
文档属性
| 名称 | 18.1 勾股定理 课件(共46张PPT) 初中数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 30.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-20 22:28:24 | ||
图片预览










文档简介
(共46张PPT)
第18章 勾股定理
义务教育沪科版数学八年级下册
18 .1
勾 股 定 理
探 究
在行距、列距都是1的方格网中,任意作出几个以格点为顶点的直角三角形,分别以三角形的各边为正方形的一边,向形外作正
方形,如图18-1.并以S1,
S2与S3;分别表示几个
正方形的面积.
图18 - 1
观察图 18-1(1),并填写:
S1=__________个单位面积;
S2=__________个单位面积;
S3=__________个单位面积.
9
9
18
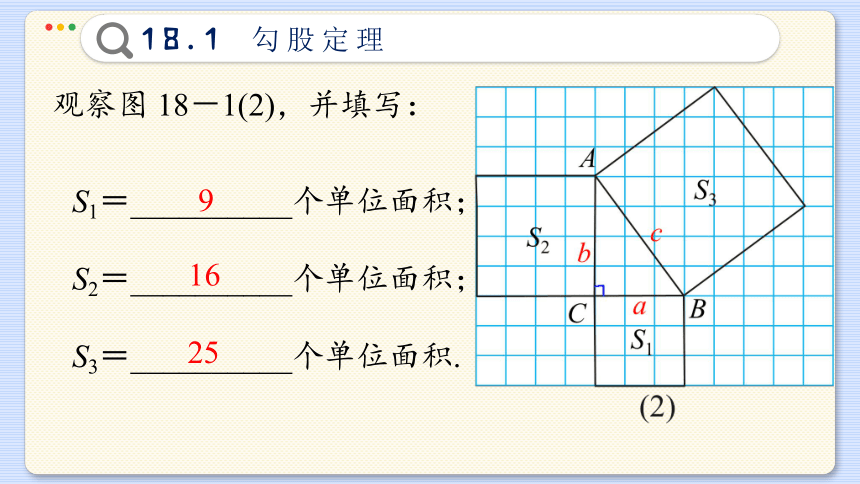
观察图 18-1(2),并填写:
S1=__________个单位面积;
S2=__________个单位面积;
S3=__________个单位面积.
9
16
25
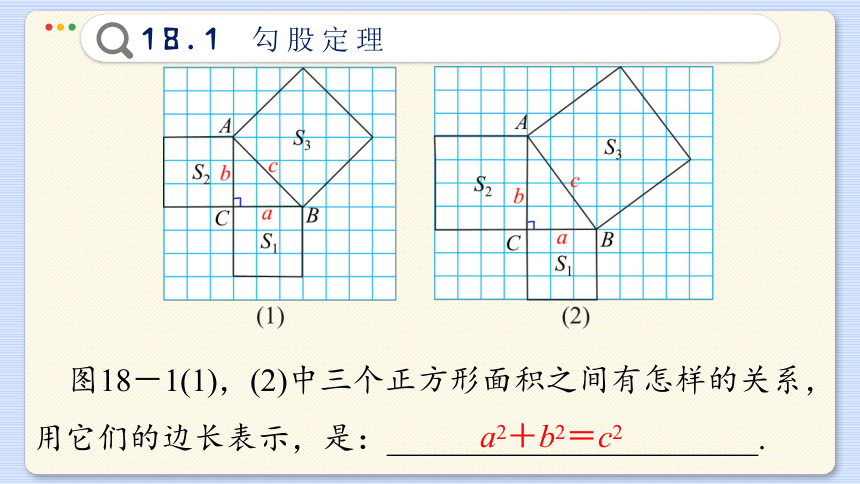
图18-1(1),(2)中三个正方形面积之间有怎样的关系,用它们的边长表示,是:_______________________.
a2+b2=c2
通过上面的探究,你能发现直角三角形三边的长之间有怎样的关系吗
定理
直角三角形两条直角边的平方和,等于斜边的平方.
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦. 因此,我们称上述定理为勾股定理国外称为毕达哥拉斯定理.
汉代数学家赵爽把勾股定理叙述成:勾股各自乘,并之为弦实,开方除之即弦.
如果直角三角形的两直角边用 a,b表示,斜边用 c 表示,那么勾股定理可表示为
a2 + b2 = c2 .
已知:如图18-2(1),在 Rt△ABC 中∠C =90°,AB =c,BC =a,AC = b.
求证:a2 + b2 = c2.
下面,用面积计算来证明这个定理.
证明 取4个与 Rt△ABC 全等的直角三角形,把它们拼成如图 18-2(2)所示的边长为 a+b的正方形 EFGH .
从图中可见,A1B1= B1C1 =C1D1=A1D1=c.
因为∠B1A1E + ∠A1B1E =90°,而 ∠A1B1E = ∠D1A1H,
因此∠B1A1E + ∠D1A1H = 90°, ∠D1A1B1 = 90°.
同理: ∠A1B1C1 = ∠B1C1D1= ∠C1D1A1 = 90°,
所以四边形A1B1C1D1,是边长为 c的正方形.
正方形 EFGH 和正方形 A1B1C1D1的面积分别记作 S正方形EFGH和 S正方形A1B1C1D1则
S正方形EFGH- 4S△ABC = S正方形A1B1C1D1
即 (a + b)2 - 4 × ab = c2 .
化简,得
a2 + b2 = c2.
例 题
例1 现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,如图 .已知云梯最多只能伸长
到10m,消防车高 3 m. 救人时云梯伸至最
长,在完成从9 m 高处救人后,还要从 12
m 高处救人,这时消防车要从原处再向着
火的楼房靠近多少米 (精确到 0.1 m)
分析:如图,设A是云梯的下端点,AB 是伸长后的云梯,B 是第一次救人的地点,D 是第二次救人的地点,过点A的水平线与楼房 ED 的交点为O.则OB =9-3=6(m),OD =12-3=9(m).
根据勾股定理,得
AO2=AB2-OB2=102-62=64.
解方程,得
AO =8(m).
设 AC =x,则 OC =8-x,于是根据勾股定理,得
OC2 + OD2 = CD2,
即 (8-x)2 + 92 = 102,
从而可以解出 x.
请根据上述分析写出解题过程.
例2 已知:如图18 - 4,在 Rt△ABC 中两直角边AC = 5,BC = 12. 求斜边上的高
CD 的长.
解 在 Rt△ABC 中,
AB2 = AC2 + BC2 = 52 + 122 = 169,
AB = = 13 .
又∵ Rt△ABC 的面积
S△ABC = AC·BC = AB·CD,
∴ CD = = = .
练 习
1. 在△ABC中,∠C=90°,AB=c,BC=a,AC=b.
(1) a = 6,b = 8,求c;
∵在Rt△ABC中,∠C = 90°,
BC = a = 6,AC = b = 8,
∴ c = AB ===10.
1. 在△ABC中,∠C=90°,AB=c,BC=a,AC=b.
(2) a = 8,c = 17,求b.
∵ 在Rt△ABC中,∠C = 90°,
BC = a = 8,AB = c = 17,
∴ b = AC = ==15.
2. 如图,楼梯的高度为 2 m,楼梯坡面的长度为 4 m,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米 (精确到0.1 m)
由题意知:∠C = 90°,AB = 4m,AC = 2m
∴BC =
==2 (m)
∴ AC + BC = 2 + 2
≈2 + 2 × 1.732 ≈ 5.5(m)
∴ 地毯的长度至少需要约5.5m.
3.(1) 如图,长3 m的梯子斜靠着墙,梯子
底端离墙底 0.6 m,问梯子顶端离地
面多少米 (精确到 0.1m)
有梯子长为3米,梯子底端距墙底为0.6米,
由所在直角三角形另一边
AC=≈2.9 (m)
(2) 题(1)中,若梯子的顶端自墙面下滑了
0.9 m,那么梯子的底端沿地面向外滑
动的距离是否也为 0.9 m 说明理由.
梯子下滑后梯子顶端距地面为
2.9 - 0.9 = 2米,
由所在直角三角形中梯子底端与墙距离为
= (m),
所以梯子的底端在水平方向上滑动为
- 0.6≠0.9。
则梯子的底端在水平方向向外滑动的距离不是0.9m.
4. 我国古代数学专著《九章算术》中记录了一个问题,其大致意思是说:有一个水面是边长为 10 尺的正方形水池,中央生长有一根芦苇,它露出水面部分高1尺,如果把它拉向最近的岸边,芦苇仍伸直而顶端恰好到达岸边的水面,求池水深和芦苇的长.(尺为当时的计量单位,1尺=m)
设水池的深度为x尺,由题意得:
x2+52= (x+1)2,
解得: x=12,
则x+1=13.
答:水深12尺,芦苇长13尺
数学天地
长度为正整数的算术平方根的线段,可以用尺规作图的方法作出来.下面介绍一种有趣的方法,你能说出其中的道理吗
取OA1=1 =,作Rt△OA1A2,使OA1 ⊥ A1A2,A1A2 = OA1 = 1,则OA2 = ,如图18-5;
图18-5
图18-5
过点 A2,在 Rt△OA1A2外作 A2A3 ⊥ OA2,且取A2A3=1,连接OA3,则 OA3=;
······
如上继续下去,可以作出长度为任一正整数的算术平方根的线段.
习题 18.1
1.在△ABC中,∠C =90°,填空:
(1) 如果AB=10, BC∶AC=3∶4,那么 BC =_______,
AC = ______;
(2) 如果 AC =1, ∠B = 30°,那么 AB =_______,
BC = _______;
6
8
2
2. 已知:在△ABC中,AB = AC = 17,BC = 16.
求 △ABC的高AD的长.
如图所示
∵AB = AC = 17
∴△ABC是等腰三角形
∵AD是△ABC的高,BC = 16.
∴BD = CD = BC = × 16 = 8
在Rt△ABD中,
∵∠ADB = 90°,AB = 17,BD = 8
∴AD = = = 15
即△ABC的高AD的长为15.
3. 已知直角三角形的三边长是三个连续自然数,求三
边长.
设三边长分别为 x-1,x ,x+1
由勾股定理可得
(x-1)2+x2= (x+1)2
解得 x1=0 (舍去) ,x2=4,
∴ 三边长分别为 3,4,5.
4. 求边长为 a 的等边三角形的面积.
作高线,由勾股定理可求高
h== a.
∴S=a·h=a·a=a2
5. 如图,从电线杆上离地面 h = 8 m 的点 A 处,向地面
拉一条长 l = 12 m 的缆绳,这条缆绳拉直后在地面上
点 B 处固定,点 B 离电线杆底部点C 的距离是多少米
(精确到 0.1 m)
由题意得:AB = 12m,AC = 8m,
∠ACB = 90°
∴ BC =
=
= 4 ≈ 8.9 (m)
∴B点离电线杆底部点C的距离是8.9m.
6. 如图,要修一个塑料蔬菜大棚,棚宽 b =3 m,高 h
=1.5 m,长l=10 m.求覆盖在顶上的长方形塑料薄膜
需要多少平方米 (精确到 0.1 m2)
根据勾股定理,得直角三角形的斜边为
= (m),
再根据长方形的面积公式,得:
× 10 ≈ 33.5 (m2)
答:覆盖在顶上的长方形塑料薄膜约需33.5平方米.
7. 如图,在甲村到乙村的公路旁有一块山地正在开发,现有A处需要爆破.已知点 A 与公路上的停靠站 B,C 的距离分别为400 m和300 m,且AC⊥AB.
为了安全起见,如果爆破点A 周围半径
250 m 的区域内不能有车辆和行人,问
在进行爆破时,公路 BC 段是否需要暂
时封闭 为什么
过A作AD⊥BC于D,
∵AC⊥AB,
∴AB2+AC2 = BC2,
∵AB =400m,AC=300m,
∴BC2 =
= = 500m
∵S△ABC = AB·AC = BC·AD
∴AD = 240m,
∵240m < 250m,
∴有危险,因此BC段公路需要暂时封闭.
本课结束
第18章 勾股定理
义务教育沪科版数学八年级下册
18 .1
勾 股 定 理
探 究
在行距、列距都是1的方格网中,任意作出几个以格点为顶点的直角三角形,分别以三角形的各边为正方形的一边,向形外作正
方形,如图18-1.并以S1,
S2与S3;分别表示几个
正方形的面积.
图18 - 1
观察图 18-1(1),并填写:
S1=__________个单位面积;
S2=__________个单位面积;
S3=__________个单位面积.
9
9
18
观察图 18-1(2),并填写:
S1=__________个单位面积;
S2=__________个单位面积;
S3=__________个单位面积.
9
16
25
图18-1(1),(2)中三个正方形面积之间有怎样的关系,用它们的边长表示,是:_______________________.
a2+b2=c2
通过上面的探究,你能发现直角三角形三边的长之间有怎样的关系吗
定理
直角三角形两条直角边的平方和,等于斜边的平方.
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦. 因此,我们称上述定理为勾股定理国外称为毕达哥拉斯定理.
汉代数学家赵爽把勾股定理叙述成:勾股各自乘,并之为弦实,开方除之即弦.
如果直角三角形的两直角边用 a,b表示,斜边用 c 表示,那么勾股定理可表示为
a2 + b2 = c2 .
已知:如图18-2(1),在 Rt△ABC 中∠C =90°,AB =c,BC =a,AC = b.
求证:a2 + b2 = c2.
下面,用面积计算来证明这个定理.
证明 取4个与 Rt△ABC 全等的直角三角形,把它们拼成如图 18-2(2)所示的边长为 a+b的正方形 EFGH .
从图中可见,A1B1= B1C1 =C1D1=A1D1=c.
因为∠B1A1E + ∠A1B1E =90°,而 ∠A1B1E = ∠D1A1H,
因此∠B1A1E + ∠D1A1H = 90°, ∠D1A1B1 = 90°.
同理: ∠A1B1C1 = ∠B1C1D1= ∠C1D1A1 = 90°,
所以四边形A1B1C1D1,是边长为 c的正方形.
正方形 EFGH 和正方形 A1B1C1D1的面积分别记作 S正方形EFGH和 S正方形A1B1C1D1则
S正方形EFGH- 4S△ABC = S正方形A1B1C1D1
即 (a + b)2 - 4 × ab = c2 .
化简,得
a2 + b2 = c2.
例 题
例1 现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,如图 .已知云梯最多只能伸长
到10m,消防车高 3 m. 救人时云梯伸至最
长,在完成从9 m 高处救人后,还要从 12
m 高处救人,这时消防车要从原处再向着
火的楼房靠近多少米 (精确到 0.1 m)
分析:如图,设A是云梯的下端点,AB 是伸长后的云梯,B 是第一次救人的地点,D 是第二次救人的地点,过点A的水平线与楼房 ED 的交点为O.则OB =9-3=6(m),OD =12-3=9(m).
根据勾股定理,得
AO2=AB2-OB2=102-62=64.
解方程,得
AO =8(m).
设 AC =x,则 OC =8-x,于是根据勾股定理,得
OC2 + OD2 = CD2,
即 (8-x)2 + 92 = 102,
从而可以解出 x.
请根据上述分析写出解题过程.
例2 已知:如图18 - 4,在 Rt△ABC 中两直角边AC = 5,BC = 12. 求斜边上的高
CD 的长.
解 在 Rt△ABC 中,
AB2 = AC2 + BC2 = 52 + 122 = 169,
AB = = 13 .
又∵ Rt△ABC 的面积
S△ABC = AC·BC = AB·CD,
∴ CD = = = .
练 习
1. 在△ABC中,∠C=90°,AB=c,BC=a,AC=b.
(1) a = 6,b = 8,求c;
∵在Rt△ABC中,∠C = 90°,
BC = a = 6,AC = b = 8,
∴ c = AB ===10.
1. 在△ABC中,∠C=90°,AB=c,BC=a,AC=b.
(2) a = 8,c = 17,求b.
∵ 在Rt△ABC中,∠C = 90°,
BC = a = 8,AB = c = 17,
∴ b = AC = ==15.
2. 如图,楼梯的高度为 2 m,楼梯坡面的长度为 4 m,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米 (精确到0.1 m)
由题意知:∠C = 90°,AB = 4m,AC = 2m
∴BC =
==2 (m)
∴ AC + BC = 2 + 2
≈2 + 2 × 1.732 ≈ 5.5(m)
∴ 地毯的长度至少需要约5.5m.
3.(1) 如图,长3 m的梯子斜靠着墙,梯子
底端离墙底 0.6 m,问梯子顶端离地
面多少米 (精确到 0.1m)
有梯子长为3米,梯子底端距墙底为0.6米,
由所在直角三角形另一边
AC=≈2.9 (m)
(2) 题(1)中,若梯子的顶端自墙面下滑了
0.9 m,那么梯子的底端沿地面向外滑
动的距离是否也为 0.9 m 说明理由.
梯子下滑后梯子顶端距地面为
2.9 - 0.9 = 2米,
由所在直角三角形中梯子底端与墙距离为
= (m),
所以梯子的底端在水平方向上滑动为
- 0.6≠0.9。
则梯子的底端在水平方向向外滑动的距离不是0.9m.
4. 我国古代数学专著《九章算术》中记录了一个问题,其大致意思是说:有一个水面是边长为 10 尺的正方形水池,中央生长有一根芦苇,它露出水面部分高1尺,如果把它拉向最近的岸边,芦苇仍伸直而顶端恰好到达岸边的水面,求池水深和芦苇的长.(尺为当时的计量单位,1尺=m)
设水池的深度为x尺,由题意得:
x2+52= (x+1)2,
解得: x=12,
则x+1=13.
答:水深12尺,芦苇长13尺
数学天地
长度为正整数的算术平方根的线段,可以用尺规作图的方法作出来.下面介绍一种有趣的方法,你能说出其中的道理吗
取OA1=1 =,作Rt△OA1A2,使OA1 ⊥ A1A2,A1A2 = OA1 = 1,则OA2 = ,如图18-5;
图18-5
图18-5
过点 A2,在 Rt△OA1A2外作 A2A3 ⊥ OA2,且取A2A3=1,连接OA3,则 OA3=;
······
如上继续下去,可以作出长度为任一正整数的算术平方根的线段.
习题 18.1
1.在△ABC中,∠C =90°,填空:
(1) 如果AB=10, BC∶AC=3∶4,那么 BC =_______,
AC = ______;
(2) 如果 AC =1, ∠B = 30°,那么 AB =_______,
BC = _______;
6
8
2
2. 已知:在△ABC中,AB = AC = 17,BC = 16.
求 △ABC的高AD的长.
如图所示
∵AB = AC = 17
∴△ABC是等腰三角形
∵AD是△ABC的高,BC = 16.
∴BD = CD = BC = × 16 = 8
在Rt△ABD中,
∵∠ADB = 90°,AB = 17,BD = 8
∴AD = = = 15
即△ABC的高AD的长为15.
3. 已知直角三角形的三边长是三个连续自然数,求三
边长.
设三边长分别为 x-1,x ,x+1
由勾股定理可得
(x-1)2+x2= (x+1)2
解得 x1=0 (舍去) ,x2=4,
∴ 三边长分别为 3,4,5.
4. 求边长为 a 的等边三角形的面积.
作高线,由勾股定理可求高
h== a.
∴S=a·h=a·a=a2
5. 如图,从电线杆上离地面 h = 8 m 的点 A 处,向地面
拉一条长 l = 12 m 的缆绳,这条缆绳拉直后在地面上
点 B 处固定,点 B 离电线杆底部点C 的距离是多少米
(精确到 0.1 m)
由题意得:AB = 12m,AC = 8m,
∠ACB = 90°
∴ BC =
=
= 4 ≈ 8.9 (m)
∴B点离电线杆底部点C的距离是8.9m.
6. 如图,要修一个塑料蔬菜大棚,棚宽 b =3 m,高 h
=1.5 m,长l=10 m.求覆盖在顶上的长方形塑料薄膜
需要多少平方米 (精确到 0.1 m2)
根据勾股定理,得直角三角形的斜边为
= (m),
再根据长方形的面积公式,得:
× 10 ≈ 33.5 (m2)
答:覆盖在顶上的长方形塑料薄膜约需33.5平方米.
7. 如图,在甲村到乙村的公路旁有一块山地正在开发,现有A处需要爆破.已知点 A 与公路上的停靠站 B,C 的距离分别为400 m和300 m,且AC⊥AB.
为了安全起见,如果爆破点A 周围半径
250 m 的区域内不能有车辆和行人,问
在进行爆破时,公路 BC 段是否需要暂
时封闭 为什么
过A作AD⊥BC于D,
∵AC⊥AB,
∴AB2+AC2 = BC2,
∵AB =400m,AC=300m,
∴BC2 =
= = 500m
∵S△ABC = AB·AC = BC·AD
∴AD = 240m,
∵240m < 250m,
∴有危险,因此BC段公路需要暂时封闭.
本课结束
