第19章 四边形小结与复习 -初中数学沪科版八年级下册课件(共74张PPT)
文档属性
| 名称 | 第19章 四边形小结与复习 -初中数学沪科版八年级下册课件(共74张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 33.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-21 09:33:00 | ||
图片预览







文档简介
(共74张PPT)
第19章 四边形
义务教育沪科版数学八年级下册
小结与复习
内容整理
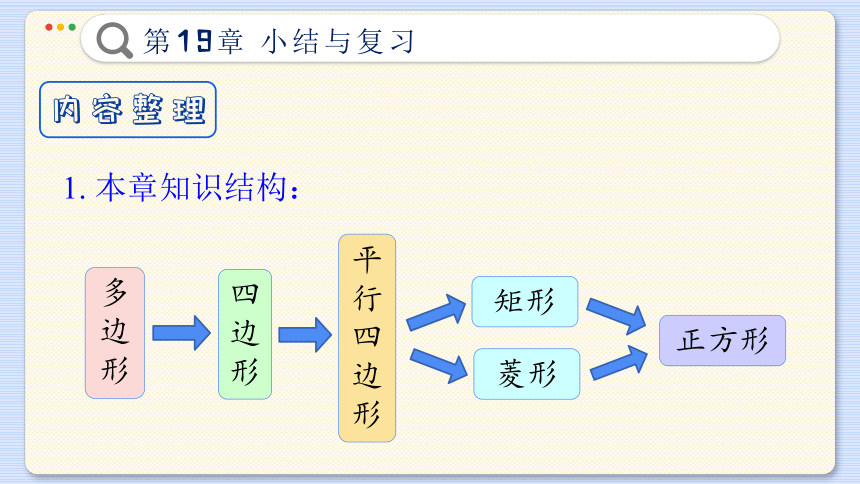
多边形
四边形
平行四边形
矩形
菱形
正方形
1. 本章知识结构:
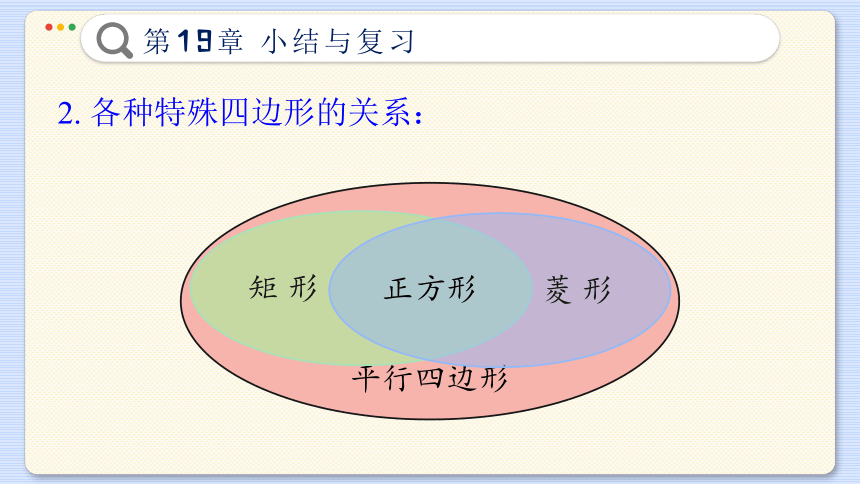
2. 各种特殊四边形的关系:
平行四边形
矩 形
菱 形
正方形
主要知识回顾
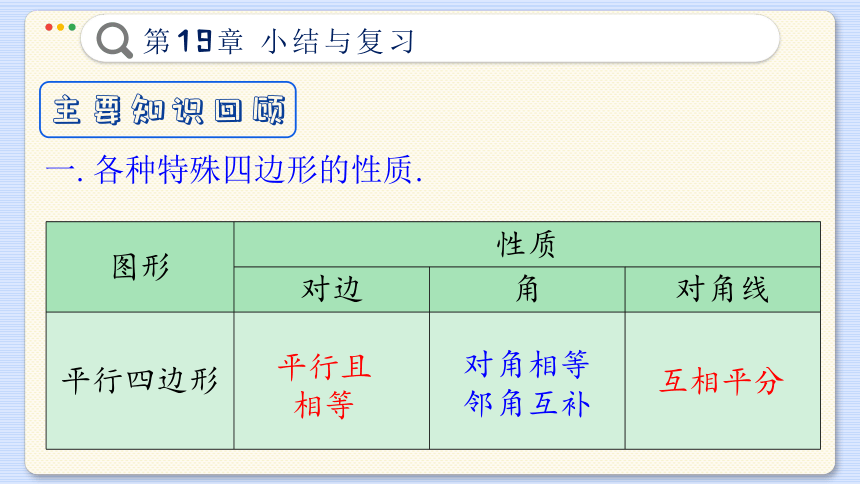
一. 各种特殊四边形的性质.
图形 性质
对边 角 对角线
平行四边形
平行且相等
对角相等
邻角互补
互相平分
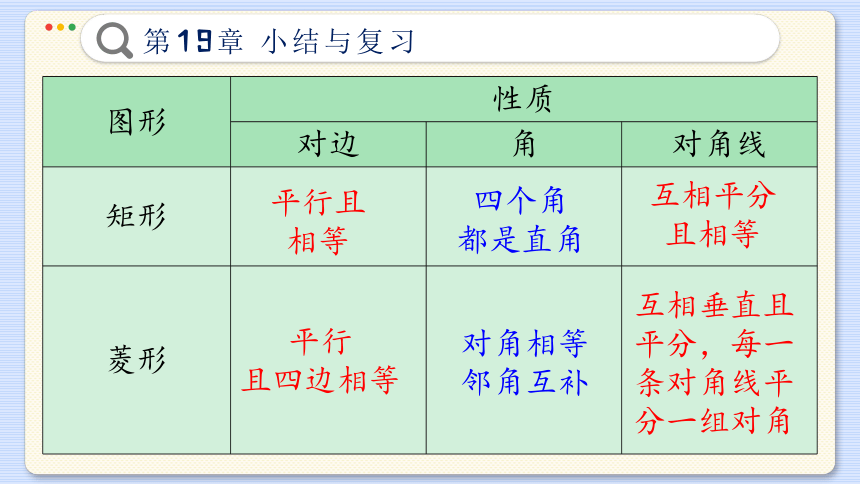
图形 性质
对边 角 对角线
矩形
菱形
平行且相等
四个角
都是直角
互相平分且相等
平行
且四边相等
对角相等
邻角互补
互相垂直且平分,每一条对角线平分一组对角
图形 性质
对边 角 对角线
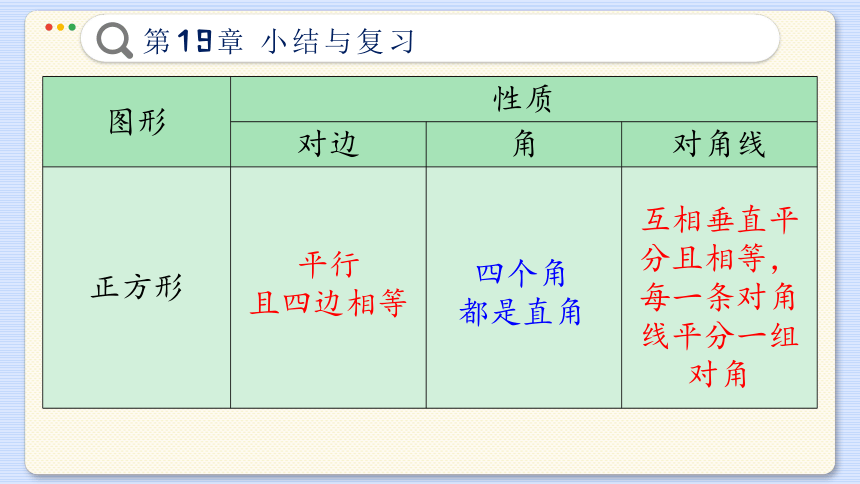
正方形
平行
且四边相等
四个角
都是直角
互相垂直平分且相等,每一条对角线平分一组对角
二、如何判定一个四边形是平行四边形、矩形、菱形、
正方形
1. 平行四边形的判定:
两组对边相等
一组对边平行且相等
对角线互相平分
两组对边分别平行(定义)
2. 矩形的判定:
①定义:有一个角是直角的平行四边形.
②定理1:对角线相等的平行四边形.
③定理2:三个角是直角的四边形.
3. 菱形的判定:
①定义:一组邻边相等的平行四边形.
②定理1:四条边都相等的四边形.
③定理2:对角线互相垂直的平行四边形.
4. 正方形的判定:
①定义:有一个角是直角且一组邻边相等的平行四边形.
②有一组邻边相等的矩形.
③有一个角是直角的菱形.
三、多边形的内角和与外角和
多边形的内角和等于 (n - 2)×180°
多边形的外角和等于 360°
正多边形每个内角的度数是
正多边形每个外角的度数是
四、三角形的中位线
1. 三角形中位线的定义:连接三角形两边中点的线段叫做三角形的中位线.
2. 三角形中位线定理:三角形两边中点连线平行于第三边,并且等于第三边的一半.
用符号语言表示:
∵ DE 是△ABC 的中位线,
∴ DE∥BC,
E
A
B
C
D
复习题
A组
1. 填空:
(1) 一个多边形的外角和是内角和的,则这个多边形的边数是_______;
(2) 一个多边形的每个外角都等于它相邻的内角,则这个多边形的边数是________,它的每个外角的度数是________.
9
4
90°
2. 四边形的内角可能都是锐角吗 可能都是直角吗 可能
都是钝角吗
四边形的四个内角不可以都是锐角,不可以都是钝角,可以都是直角.
因为四边形的内角和为360°
如果四个内角都是锐角或都是钝角则内角和小于360°或大于360°,与四边形的内角和为360°矛盾.
所以四个内角不可以都是锐角或都是钝角.
若四个内角都是直角,则四个内角的和等于360°与内角和定理相符,
所以四个内角可以都是直角.
3. 是否存在一个多边形,它的每个内角都等于相邻外角
的3倍 并简述你的理由
存在.
设该多边形一个外角为x°,则相邻的内角是3x°,
根据多边形内角和相邻外角的关系(邻补角)得:
x°+3x°=180°.
∴ x=45,
∴ 该多边形边数为:360°÷45°=8
(多边形外角和定理),
∴ 正八边形的每个内角都等于相邻外角的3倍.
综上所述:存在一个多边形,它的每个内角都等于相邻外角的3倍.
4. 已知:如图,在 ABCD 中,AE = CF,点M,N是
ED,BF的中点.
求证:四边形MFNE 是平行四边形.
证明:∵四边形ABCD是平行四边形.
∴∠A=∠C,AD=BC.
又∵ AE= CF.
∴ △AED≌△CFB.
∴ DE = BF,∠ADE = ∠CBF.
∵ M、N是ED、BF的中点.
∴ EM=FN.
∵ AB∥DC.
∴ ∠AED =∠CDE
又∵ ∠ADE = ∠CBF,
∠ABC = ∠ADC.
∴ ∠ABF = ∠CDE.
∴ ∠AED = ∠ABF.
∴ ED ∥ BF. 即 EM ∥ FN.
∴ 四边形MFNE 是平行四边形(一组对边平行且相等的四边形是平行四边形).
5. 已知:如图,在 ABCD中,点O是对角线AC 的中
点EF 经过点O分别与AB,CD 交于点 F,E.
求证:OE = OF.
证明:∵四边形ABCD是平行四边形.
∴AB ∥ CD.
∴∠CAB = ∠ACD,
∵ O是对角线AC的中点.
∴AO = CO.
在△AOF和△COE中
∠CAB = ∠ACD,
CO = AO,
∠EOC = ∠FOA.
∴ △COE ≌ △AOF (ASA),
∴ EO = FO.
6. 将一张长40 cm宽20 cm 的矩形纸片剪成长为18 cm、
宽为12cm 的矩形纸片,问最多能剪几个
答: 最多可以剪3个.
∵ 20×40 ÷ 18×12 ≈ 3.7.
∴ 结合长和宽可知最多剪3个,如下图.
7. 如图,在 ABCD 中,AE 平分∠BAD,交 BC 于点
E,EF // AB,交AD于点F. 试问四边形ABEF 是菱形
吗 说明你的理由.
四边形ABEF是菱形.
理由:
∵四边形ABCD是平行四边形.
∴AF ∥ BE
∴∠FAE = ∠BEA
∵ EF ∥ AB
∴ 四边形ABEF是平行四边形
∵∠EAF = ∠EAB
∴∠BEA = ∠EAB
∴ BA = BE
∴四边形ABEF是菱形.
8. 某地有四个村庄 A,B,C,D,它们正好位于一个正
方形的四个顶点. 现在四个村庄计划联合架设一条电
话线路,他们设计了 4 种架设方案,如图中的实线
部分. 请你帮助计算一下,哪种架设方案最省电线.
设正方形的边长为1,则有:
(1) 电线长为:
AD+AB+BC=1+1+1=3;
(2)∵∠C =90°,
由勾股定理得:
BD=== .
∴电线长为:
AB+CD+BD = 1+1+= 2+≈3.41;
(3)∵∠ABC =∠BCD =90°
由勾股定理得:
AC=BD= = = ,
∴电线长为:
BD + AC = + = 2 ≈ 2.82;
(4) 分别过点E,F作EM⊥AD,FN⊥BC
垂足分别为M,N,如图:
M
N
∵∠DAE =∠ADE =30°
∠FBC =∠FCB =30°.
∴AE = DE,BF =CF
∴AM = DM =AD= .
M
N
∴ AE = DE == =,
ME = AE = × = .
同理: BF = CF = =,
FN = BF = .
M
N
则 EF=MN-EM-EN=1-2×
=1 - .
∴电线长为:
AE+DE+BF+CF + EF
= 4 × + (1 - )
= 1 + ≈ 2.732
∵ 2.732 < 2.82 <3< 3.41,
∴第四种最省电线.
9. 如图,在正方形 ABCD 中,点 E,F 是边 BC,CD 上
的点,且BE = CF. 那么,线段AE 与 BF的夹角有多大
为什么
90°.
理由如下:
在正方形ABCD中,
AB = BC,∠ABE =∠BCF.
∵ BE =CF.
∴△ABE ≌△BCF
∴∠AEB= ∠BFC,
∠EAB = ∠FBC.
∵∠BFC +∠FBC
=∠AEB +∠EAB =90°.
∴∠AEB +∠FBC =90°.
∴AE ⊥BF.
∴线段AE与BF的夹角是90°.
复习题
B组
1. 一个多边形的内角中,最多有几个锐角 为什么
一个多边形的内角中,最多有3个锐角.
理由是:因为多边形的外角和是360度,在外角中最多有3个钝角,如果超过3个,则和一定大于360度,多边形的内角与外角互为邻补角.
所以外角中最多有3个钝角,内角中就最多有3个锐角.
2. 已知:如图 ABCD 的顶点 D在 AEFG 的边 FG
上, AEFG的顶点 E 在 ABCD 的边 BC上.
求证:S ABCD = S AEFG·
证明:连结DE,过点D作DN⊥AE于点N,过点E作EM⊥AD于点M.
N
M
在△ADE中:
S△ADE=×AD×EM= ×AE×DN.
∴ AD × EM = AE × DN.
N
M
在平行四边形中: S□ABCD = AD × EM.
在平行四边形中: S□ABFG = AE × DN.
∴S□ABCD = S□AEFG.
3. 已知:点 M,N分别是 ABCD 的边 AB,CD 的中点
CM交 BD 于点 E,AN 交 BD 于点 F.
求证:BE = EF = FD.
证明:在平行四边形ABCD中,
∴ AB∥CD,AB=CD.
∴△AFB ~ △NFD.
∴DF∶ BF=DN∶AB,
∵N为DC的中点,
∴DF∶BF=DN∶AB=1∶2,
即DF=BD,
同理BE= BD,
则 EF = BD-DF-BE
= BD - BD - BD
= BD ,
∴ DF = EF = BE.
4. 已知点O是矩形 ABCD 内任一点. 求证:OA2 +OC2
= OB2 +OD2. 如果点O在矩形ABCD的外部,结论
还成立吗
证明:当O在矩形ABCD的内部时,如图,
过O作OM ⊥ AD于M,
延长MO交BC于N,
则∠AMO = ∠DMO =
∠CNO = ∠ BNO = 90°,
∵四边形ABCD是矩形,
∴ ∠DAB = ∠ABC = ∠BCD = ∠ADC = 90°,
∴ 四边形ABNM和四边形DCNM是矩形,
M
N
∴ AM = BN,DM = CN,
由勾股定理得:
OA2 + OC2 =AM2 + OM2 +CN2+ON2
OB2 + OD2 = BN2 + ON2 +DM2+OM2
∴ OA2+OC2=OB2+OD2;
M
N
当O在矩形ABCD的外部时,
OA2+OC2=OB2+OD2 还成立,
O
O
理由是:
过O作OM⊥AD于M,
延长OM交BC于N,如图,
则∠AMN = ∠DMN =∠CNM
= ∠BNM = 90°,
∵四边形ABCD是矩形,
∴∠DAB =∠ABC =∠BCD =∠ADC = 90°,
M
N
∴四边形ABNM和四边形DCNM是矩形,
∴AM = BN,DM = CN,
由勾股定理得:
OA2 + OC2 = AM2 + OM2
+ CN2+ON2,
OB2+OD2 = BN2+ON2
+DM2+OM2.
∴OA2+OC2 = OB2+OD2.
O
M
N
5. 在△ABC 中,BD,CE 是两条高,点P,Q 分别是BC,
ED 的中点. 求证:PQ ⊥ED .
证明:作出图形,
连结PE、PD.
∵ BD⊥AC,P为BC的中点.
∴DP= BC.
(直角三角形斜边上的中线等于斜边的一半)
同理:EP= BC.
∴DP = EP.
△EPD为等腰三角形.
∵Q为ED的中点.
∴PQ ⊥ ED. (三线合一)
复习题
C组
1. 设四边形 ABCD 的每一个顶点到其他 3 个顶点的距离
之和都相等. 这个四边形是什么四边形 请说明理由.
四边形ABCD是矩形,
理由如下:
由题意得,
AB+AD+AC
=DA+DB+DC
=DC+CB+AC
=BA+BC+BD.
∴AB=CD,AD=BC,AC=BD,
∴四边形ABCD为矩形
2. 证明:在 ABCD中,AC2+BD2=2(AB2+BC2).
如图所示:
过A作AE⊥BC于E,
过D作DF⊥BC,
交BC延长线于F,
E
F
∵四边形ABCD是平行四边形,
∴ AB=CD,∠ABE =∠DCF
又∵∠AEB=∠DFC =90°
∴△ABE≌△DCF。
∴ AE=DF, BE=CF
∵AC2 =AE2+CE2+BF2,
BD2=DF2+BF2
∴ AC2+BD2= (AE2+CE2)+(DF2+BF2)
= AE2+(BC-BE)2+AE2+(BC+CF)2
=2AE2+BC2-2BC·BE+BE2+BC2 +2BC·BE+BE2
=2AE2+2BE2 +2BC2
=2(AE2+BE2) +2BC2
=2AB2+2BC2
=2(AB2+BC2)
故在□ABCD中,AC2+BD2=2(AB2 + BC2).
3. 已知:如图,在矩形内一些相交线把它分成 8 个部分,
其中的3个部分面积分别为 13,35,49. 求图中阴影
部分的面积.
x
y
x
y
∵(35 +x +49) +(13 + y) =长方形面积的一半,
又∵长方形面积的一半= x +S阴影+ y,
∴ S阴影=35+49 +13=97.
4. (1) 如图(1),从ABCD 的顶点 A,B,C,D,向形外的
任意直线 MN作垂线AA′,BB′,CC′,DD′,垂足是
点A′,B′,C′,D′.
求证:AA′+ CC′ = BB′ + DD′ .
证明: 记点O为平行四边形ABCD两条对角线的交点,作OO′ ⊥ MN,垂足为 O′.
O
O′
∵在平行四边形ABCD中,
AO = OC,AA′∥OO′∥CC′,
∴OO′是梯形AA′CC′的中位线.
∴ OO′ =(AA′ + CC′),
同理可证 OO′ =(BB′ + DD′).
∴ AA′ + CC′ = BB′ + DD′ .
O
O′
(2) 如图(2),将直线 MN 向上平移,使得点A 在直线一
侧,点 B,C,D 三点在直线的另一侧,这时,从
点 A,B,C,D 向直线 MN作垂线,
垂足分别为点 A′,B′,C′,D′,
那么垂线段AA′,BB′,CC′,
DD′之间存在什么关系
CC′=AA′+BB′+DD′
证明:记点O为平行四边形ABCD两
条对角线的交点,
作 OO′⊥MN,垂足为 O′.
同样可得 OO′= (BB′ +DD′).
连结AC′,延长OO′交AC′于H.
∵ O为AC的中点,OO′ ∥ AA′ ∥ CC′.
O
O′
H
O
O′
H
∴ OH为ACC′的中位线,O′H为AA′C′的中位线.
∴ OH= CC′,O′H= AA′.
∴ OO′ =OH-O′H =(CC′-AA′).
综上,CC′ - AA′ = BB′ + DD′,
即CC′ = AA′ + BB′ + DD′.
(3) 如图(3),再将直线 MN 向上平行移动,使两侧各有
两个顶点,从点 A,B,C,D向直线 MN作的垂线
段AA′,BB′,CC′,DD′,它们之间
又有什么关系 根据图(2)、
图(3)写出你的猜想,
并加以证明.
AA' + DD′ = BB′ + CC′
证明:记点O为平行四边形ABCD两条对角线的
交点,作OO′⊥MN,垂足为 O′.
连结AC′,延长OO′交AC′于H.
同样可得OO′ = OH - OH′
= (CC′ - AA′)
连结D′B,延长OO′交D′B于G.
O
O′
H
G
类似推理可以得到:
OO′ = OG - O′G
= (DD′ - BB′).
∴ CC′ - AA′ = DD′ - BB′.
即AA′ + DD′ = BB′ + CC′.
O
O′
H
G
本课结束
第19章 四边形
义务教育沪科版数学八年级下册
小结与复习
内容整理
多边形
四边形
平行四边形
矩形
菱形
正方形
1. 本章知识结构:
2. 各种特殊四边形的关系:
平行四边形
矩 形
菱 形
正方形
主要知识回顾
一. 各种特殊四边形的性质.
图形 性质
对边 角 对角线
平行四边形
平行且相等
对角相等
邻角互补
互相平分
图形 性质
对边 角 对角线
矩形
菱形
平行且相等
四个角
都是直角
互相平分且相等
平行
且四边相等
对角相等
邻角互补
互相垂直且平分,每一条对角线平分一组对角
图形 性质
对边 角 对角线
正方形
平行
且四边相等
四个角
都是直角
互相垂直平分且相等,每一条对角线平分一组对角
二、如何判定一个四边形是平行四边形、矩形、菱形、
正方形
1. 平行四边形的判定:
两组对边相等
一组对边平行且相等
对角线互相平分
两组对边分别平行(定义)
2. 矩形的判定:
①定义:有一个角是直角的平行四边形.
②定理1:对角线相等的平行四边形.
③定理2:三个角是直角的四边形.
3. 菱形的判定:
①定义:一组邻边相等的平行四边形.
②定理1:四条边都相等的四边形.
③定理2:对角线互相垂直的平行四边形.
4. 正方形的判定:
①定义:有一个角是直角且一组邻边相等的平行四边形.
②有一组邻边相等的矩形.
③有一个角是直角的菱形.
三、多边形的内角和与外角和
多边形的内角和等于 (n - 2)×180°
多边形的外角和等于 360°
正多边形每个内角的度数是
正多边形每个外角的度数是
四、三角形的中位线
1. 三角形中位线的定义:连接三角形两边中点的线段叫做三角形的中位线.
2. 三角形中位线定理:三角形两边中点连线平行于第三边,并且等于第三边的一半.
用符号语言表示:
∵ DE 是△ABC 的中位线,
∴ DE∥BC,
E
A
B
C
D
复习题
A组
1. 填空:
(1) 一个多边形的外角和是内角和的,则这个多边形的边数是_______;
(2) 一个多边形的每个外角都等于它相邻的内角,则这个多边形的边数是________,它的每个外角的度数是________.
9
4
90°
2. 四边形的内角可能都是锐角吗 可能都是直角吗 可能
都是钝角吗
四边形的四个内角不可以都是锐角,不可以都是钝角,可以都是直角.
因为四边形的内角和为360°
如果四个内角都是锐角或都是钝角则内角和小于360°或大于360°,与四边形的内角和为360°矛盾.
所以四个内角不可以都是锐角或都是钝角.
若四个内角都是直角,则四个内角的和等于360°与内角和定理相符,
所以四个内角可以都是直角.
3. 是否存在一个多边形,它的每个内角都等于相邻外角
的3倍 并简述你的理由
存在.
设该多边形一个外角为x°,则相邻的内角是3x°,
根据多边形内角和相邻外角的关系(邻补角)得:
x°+3x°=180°.
∴ x=45,
∴ 该多边形边数为:360°÷45°=8
(多边形外角和定理),
∴ 正八边形的每个内角都等于相邻外角的3倍.
综上所述:存在一个多边形,它的每个内角都等于相邻外角的3倍.
4. 已知:如图,在 ABCD 中,AE = CF,点M,N是
ED,BF的中点.
求证:四边形MFNE 是平行四边形.
证明:∵四边形ABCD是平行四边形.
∴∠A=∠C,AD=BC.
又∵ AE= CF.
∴ △AED≌△CFB.
∴ DE = BF,∠ADE = ∠CBF.
∵ M、N是ED、BF的中点.
∴ EM=FN.
∵ AB∥DC.
∴ ∠AED =∠CDE
又∵ ∠ADE = ∠CBF,
∠ABC = ∠ADC.
∴ ∠ABF = ∠CDE.
∴ ∠AED = ∠ABF.
∴ ED ∥ BF. 即 EM ∥ FN.
∴ 四边形MFNE 是平行四边形(一组对边平行且相等的四边形是平行四边形).
5. 已知:如图,在 ABCD中,点O是对角线AC 的中
点EF 经过点O分别与AB,CD 交于点 F,E.
求证:OE = OF.
证明:∵四边形ABCD是平行四边形.
∴AB ∥ CD.
∴∠CAB = ∠ACD,
∵ O是对角线AC的中点.
∴AO = CO.
在△AOF和△COE中
∠CAB = ∠ACD,
CO = AO,
∠EOC = ∠FOA.
∴ △COE ≌ △AOF (ASA),
∴ EO = FO.
6. 将一张长40 cm宽20 cm 的矩形纸片剪成长为18 cm、
宽为12cm 的矩形纸片,问最多能剪几个
答: 最多可以剪3个.
∵ 20×40 ÷ 18×12 ≈ 3.7.
∴ 结合长和宽可知最多剪3个,如下图.
7. 如图,在 ABCD 中,AE 平分∠BAD,交 BC 于点
E,EF // AB,交AD于点F. 试问四边形ABEF 是菱形
吗 说明你的理由.
四边形ABEF是菱形.
理由:
∵四边形ABCD是平行四边形.
∴AF ∥ BE
∴∠FAE = ∠BEA
∵ EF ∥ AB
∴ 四边形ABEF是平行四边形
∵∠EAF = ∠EAB
∴∠BEA = ∠EAB
∴ BA = BE
∴四边形ABEF是菱形.
8. 某地有四个村庄 A,B,C,D,它们正好位于一个正
方形的四个顶点. 现在四个村庄计划联合架设一条电
话线路,他们设计了 4 种架设方案,如图中的实线
部分. 请你帮助计算一下,哪种架设方案最省电线.
设正方形的边长为1,则有:
(1) 电线长为:
AD+AB+BC=1+1+1=3;
(2)∵∠C =90°,
由勾股定理得:
BD=== .
∴电线长为:
AB+CD+BD = 1+1+= 2+≈3.41;
(3)∵∠ABC =∠BCD =90°
由勾股定理得:
AC=BD= = = ,
∴电线长为:
BD + AC = + = 2 ≈ 2.82;
(4) 分别过点E,F作EM⊥AD,FN⊥BC
垂足分别为M,N,如图:
M
N
∵∠DAE =∠ADE =30°
∠FBC =∠FCB =30°.
∴AE = DE,BF =CF
∴AM = DM =AD= .
M
N
∴ AE = DE == =,
ME = AE = × = .
同理: BF = CF = =,
FN = BF = .
M
N
则 EF=MN-EM-EN=1-2×
=1 - .
∴电线长为:
AE+DE+BF+CF + EF
= 4 × + (1 - )
= 1 + ≈ 2.732
∵ 2.732 < 2.82 <3< 3.41,
∴第四种最省电线.
9. 如图,在正方形 ABCD 中,点 E,F 是边 BC,CD 上
的点,且BE = CF. 那么,线段AE 与 BF的夹角有多大
为什么
90°.
理由如下:
在正方形ABCD中,
AB = BC,∠ABE =∠BCF.
∵ BE =CF.
∴△ABE ≌△BCF
∴∠AEB= ∠BFC,
∠EAB = ∠FBC.
∵∠BFC +∠FBC
=∠AEB +∠EAB =90°.
∴∠AEB +∠FBC =90°.
∴AE ⊥BF.
∴线段AE与BF的夹角是90°.
复习题
B组
1. 一个多边形的内角中,最多有几个锐角 为什么
一个多边形的内角中,最多有3个锐角.
理由是:因为多边形的外角和是360度,在外角中最多有3个钝角,如果超过3个,则和一定大于360度,多边形的内角与外角互为邻补角.
所以外角中最多有3个钝角,内角中就最多有3个锐角.
2. 已知:如图 ABCD 的顶点 D在 AEFG 的边 FG
上, AEFG的顶点 E 在 ABCD 的边 BC上.
求证:S ABCD = S AEFG·
证明:连结DE,过点D作DN⊥AE于点N,过点E作EM⊥AD于点M.
N
M
在△ADE中:
S△ADE=×AD×EM= ×AE×DN.
∴ AD × EM = AE × DN.
N
M
在平行四边形中: S□ABCD = AD × EM.
在平行四边形中: S□ABFG = AE × DN.
∴S□ABCD = S□AEFG.
3. 已知:点 M,N分别是 ABCD 的边 AB,CD 的中点
CM交 BD 于点 E,AN 交 BD 于点 F.
求证:BE = EF = FD.
证明:在平行四边形ABCD中,
∴ AB∥CD,AB=CD.
∴△AFB ~ △NFD.
∴DF∶ BF=DN∶AB,
∵N为DC的中点,
∴DF∶BF=DN∶AB=1∶2,
即DF=BD,
同理BE= BD,
则 EF = BD-DF-BE
= BD - BD - BD
= BD ,
∴ DF = EF = BE.
4. 已知点O是矩形 ABCD 内任一点. 求证:OA2 +OC2
= OB2 +OD2. 如果点O在矩形ABCD的外部,结论
还成立吗
证明:当O在矩形ABCD的内部时,如图,
过O作OM ⊥ AD于M,
延长MO交BC于N,
则∠AMO = ∠DMO =
∠CNO = ∠ BNO = 90°,
∵四边形ABCD是矩形,
∴ ∠DAB = ∠ABC = ∠BCD = ∠ADC = 90°,
∴ 四边形ABNM和四边形DCNM是矩形,
M
N
∴ AM = BN,DM = CN,
由勾股定理得:
OA2 + OC2 =AM2 + OM2 +CN2+ON2
OB2 + OD2 = BN2 + ON2 +DM2+OM2
∴ OA2+OC2=OB2+OD2;
M
N
当O在矩形ABCD的外部时,
OA2+OC2=OB2+OD2 还成立,
O
O
理由是:
过O作OM⊥AD于M,
延长OM交BC于N,如图,
则∠AMN = ∠DMN =∠CNM
= ∠BNM = 90°,
∵四边形ABCD是矩形,
∴∠DAB =∠ABC =∠BCD =∠ADC = 90°,
M
N
∴四边形ABNM和四边形DCNM是矩形,
∴AM = BN,DM = CN,
由勾股定理得:
OA2 + OC2 = AM2 + OM2
+ CN2+ON2,
OB2+OD2 = BN2+ON2
+DM2+OM2.
∴OA2+OC2 = OB2+OD2.
O
M
N
5. 在△ABC 中,BD,CE 是两条高,点P,Q 分别是BC,
ED 的中点. 求证:PQ ⊥ED .
证明:作出图形,
连结PE、PD.
∵ BD⊥AC,P为BC的中点.
∴DP= BC.
(直角三角形斜边上的中线等于斜边的一半)
同理:EP= BC.
∴DP = EP.
△EPD为等腰三角形.
∵Q为ED的中点.
∴PQ ⊥ ED. (三线合一)
复习题
C组
1. 设四边形 ABCD 的每一个顶点到其他 3 个顶点的距离
之和都相等. 这个四边形是什么四边形 请说明理由.
四边形ABCD是矩形,
理由如下:
由题意得,
AB+AD+AC
=DA+DB+DC
=DC+CB+AC
=BA+BC+BD.
∴AB=CD,AD=BC,AC=BD,
∴四边形ABCD为矩形
2. 证明:在 ABCD中,AC2+BD2=2(AB2+BC2).
如图所示:
过A作AE⊥BC于E,
过D作DF⊥BC,
交BC延长线于F,
E
F
∵四边形ABCD是平行四边形,
∴ AB=CD,∠ABE =∠DCF
又∵∠AEB=∠DFC =90°
∴△ABE≌△DCF。
∴ AE=DF, BE=CF
∵AC2 =AE2+CE2+BF2,
BD2=DF2+BF2
∴ AC2+BD2= (AE2+CE2)+(DF2+BF2)
= AE2+(BC-BE)2+AE2+(BC+CF)2
=2AE2+BC2-2BC·BE+BE2+BC2 +2BC·BE+BE2
=2AE2+2BE2 +2BC2
=2(AE2+BE2) +2BC2
=2AB2+2BC2
=2(AB2+BC2)
故在□ABCD中,AC2+BD2=2(AB2 + BC2).
3. 已知:如图,在矩形内一些相交线把它分成 8 个部分,
其中的3个部分面积分别为 13,35,49. 求图中阴影
部分的面积.
x
y
x
y
∵(35 +x +49) +(13 + y) =长方形面积的一半,
又∵长方形面积的一半= x +S阴影+ y,
∴ S阴影=35+49 +13=97.
4. (1) 如图(1),从ABCD 的顶点 A,B,C,D,向形外的
任意直线 MN作垂线AA′,BB′,CC′,DD′,垂足是
点A′,B′,C′,D′.
求证:AA′+ CC′ = BB′ + DD′ .
证明: 记点O为平行四边形ABCD两条对角线的交点,作OO′ ⊥ MN,垂足为 O′.
O
O′
∵在平行四边形ABCD中,
AO = OC,AA′∥OO′∥CC′,
∴OO′是梯形AA′CC′的中位线.
∴ OO′ =(AA′ + CC′),
同理可证 OO′ =(BB′ + DD′).
∴ AA′ + CC′ = BB′ + DD′ .
O
O′
(2) 如图(2),将直线 MN 向上平移,使得点A 在直线一
侧,点 B,C,D 三点在直线的另一侧,这时,从
点 A,B,C,D 向直线 MN作垂线,
垂足分别为点 A′,B′,C′,D′,
那么垂线段AA′,BB′,CC′,
DD′之间存在什么关系
CC′=AA′+BB′+DD′
证明:记点O为平行四边形ABCD两
条对角线的交点,
作 OO′⊥MN,垂足为 O′.
同样可得 OO′= (BB′ +DD′).
连结AC′,延长OO′交AC′于H.
∵ O为AC的中点,OO′ ∥ AA′ ∥ CC′.
O
O′
H
O
O′
H
∴ OH为ACC′的中位线,O′H为AA′C′的中位线.
∴ OH= CC′,O′H= AA′.
∴ OO′ =OH-O′H =(CC′-AA′).
综上,CC′ - AA′ = BB′ + DD′,
即CC′ = AA′ + BB′ + DD′.
(3) 如图(3),再将直线 MN 向上平行移动,使两侧各有
两个顶点,从点 A,B,C,D向直线 MN作的垂线
段AA′,BB′,CC′,DD′,它们之间
又有什么关系 根据图(2)、
图(3)写出你的猜想,
并加以证明.
AA' + DD′ = BB′ + CC′
证明:记点O为平行四边形ABCD两条对角线的
交点,作OO′⊥MN,垂足为 O′.
连结AC′,延长OO′交AC′于H.
同样可得OO′ = OH - OH′
= (CC′ - AA′)
连结D′B,延长OO′交D′B于G.
O
O′
H
G
类似推理可以得到:
OO′ = OG - O′G
= (DD′ - BB′).
∴ CC′ - AA′ = DD′ - BB′.
即AA′ + DD′ = BB′ + CC′.
O
O′
H
G
本课结束
