第17章 一元二次方程 小结与复习 -初中数学沪科版八年级下册课件(共50张PPT)
文档属性
| 名称 | 第17章 一元二次方程 小结与复习 -初中数学沪科版八年级下册课件(共50张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 39.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-21 09:34:29 | ||
图片预览











文档简介
(共50张PPT)
第17章 一元二次方程
义务教育沪科版数学八年级下册
小结与复习
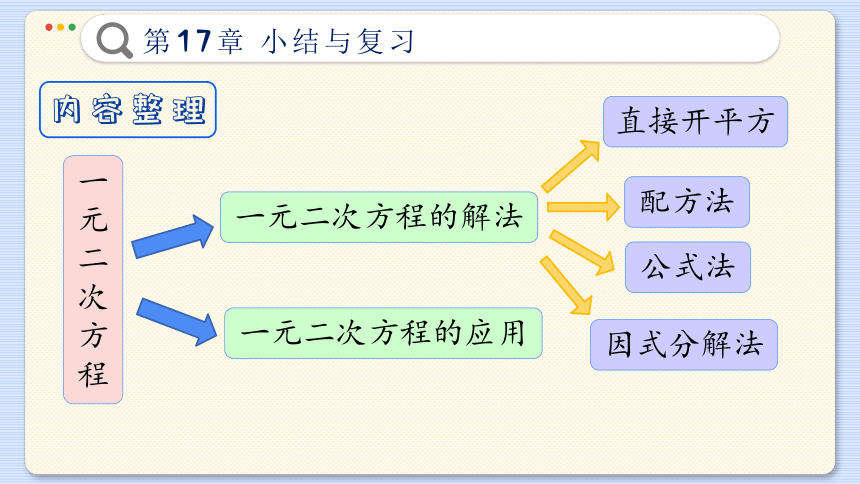
内容整理
一元二次方程
一元二次方程的解法
直接开平方
一元二次方程的应用
配方法
公式法
因式分解法
主要知识回顾
1. 一元二次方程
一般形式是 ax +bx+c=0,其中a≠0 .
只含有一个未知数,并且未知数的最高次数是 2 的整式方程,叫做一元二次方程.
2. 一元二次方程的解法有:
一元二次方程的解法 适用的方程类型
直接开平方法
配方法
公式法
因式分解
x2 + px + q = 0 ( p2 - 4q≥0)
(ax + m)2 = n (a ≠ 0,n≥0)
ax2 + bx +c = 0 (a ≠ 0,b2 - 4ac≥0)
(ax + m)(bx + n) = 0 (ab ≠ 0)
3. 一元二次方程根的判别式有什么作用
一元二次方程 ax +bx+c=0,辨别式为:
△=b2-4ac .
△ >0时,方程有两个不相等的实数根;
△ = 0时,方程有两个相等的实数根;
△ < 0时,方程无实数根 .
*4. 一元二次方程的根与系数有怎样的关系
设 x1,x2 是方程 ax +bx+c=0 的两个根,
x1 + x2 = -
x1 · x2 =
复习题
A组
1. 解下列方程:
(1) x2 = 64;
(2) x2 = 8;
x=±.
x = ± 8
即 x1 = 8,
x2 =- 8
x=±.
x = ±2
即x1 = 2,
x2 =- 2
(3) (3x+2)2 = 4(x-3)2;
(3x+2)2 -4(x-3)2=0
[3x+2+2(x-3)][3x+2-2(x-3)] =0
(5x-4)(x+8) =0
5x-4=0 或 x+8=0
x1=,x2=-8
(4) y2 -3y =0;
y (y -3) =0
y=0 或y -3 =0
解得:y1 = 0,
y2 =
(5) (2x +1)2 = 2x +1.
(2x +1)2 -2x +1=0
[(2x +1) -1](2x +1) =0
2x(2x+1) =0
2x=0或2x+1=0
解得: x1=0,x2=-
2. 用配方法解下列方程:
(1) x2-x-1 = 0;
(2) 3x2 =-1-5x ;
(3) 5y -84 +y2 =0;
(4) 2x2+x =3.
3. 用公式法解下列方程:
(1) x2+2 = 2x;
(2) 9x2 + 4 = 12x;
(3) (2x -1)2 -5 = x(x -5);
(4) y - = 1 .
4. 用适当方法解下列方程:
(1) x2 + 6x - 5 = 0;
(2) (x + 3)(x - 3) = 2;
(3) (t - )2 + 4t = 0;
(4) 3x(x - 1) = 2 - 2x.
5. 已知关于x的方程 2x2 - 5x + k = 0的一个根是 1.
(1) 求k的值;
(2) 解这个方程.
6. 设 x1,x2 是方程 2x2 +5x -7 =0 的两个根,不解方
程,求下列式子的值.
(1) x12 + x22 ;
(2) + .
7. 有一块长 25 cm宽 15 cm 的长方形硬纸板,如果在纸
板的四个角上各截去一个相同大小的小正方形,然后
把四边折起来,做成一个底面积为 231 cm2的无盖长
方体盒子.求截去的小正方形的边长.
8. 某商厦 10 月份的营业额是 50 万元,第四季度的营业
额是 182 万元问. 第四季度后两个月的月平均营业额
的增长率是多少
复习题
B组
1. 已知 y = x2 - 2x - 3.
(1) x 是什么数时,y = 0
1. 已知 y = x2 - 2x - 3.
(2) x 是什么数时,y = - 4
2. 有三个连续奇数,已知它们的平方和等于251,求这
三个数.
3. 已知:关于x的一元二次方程 (b - c)x2 + (c - a)x +(a-b) = 0 有两个相等的实数根. 求证:2b = a + c.
证明:因为方程有两个相等的实数根,
所以(c-a)2-4(b-c)(a-b) =0。
整理得(c+a-2b) =0,
所以2b=a+c。
4. 要建一个面积为 150 m2 的长方形养鸡场,为了节省
材料,养鸡场的一边利用原有的一道墙,另三边用铁
丝网围成,如果铁丝网的长为 35 m.
(1) 若墙足够长,则养鸡场的长与宽各为多少
设垂直于墙的边长为 x m,则平行于墙的边长为(35-2x)m,
依题意,得:x(35-2x) =150,
整理,得:2x2-35x+150=0,
解得: x1=7.5,x2=10,
∴35-2x=20或35-2x=15.
答:养鸡场的长为20m或15m,宽为7.5m或10m.
(2) 若给定墙长为 a m,则墙长 a 对题目的解是否有影响
当a < 15时,题目无解;
当15 ≤ a < 20时,题目只有一个解;
当a ≥ 20时,题目有两个解.
5. 如图,OA=OB=50cm,OC 是一条射线,OC ⊥AB,
一小虫由点 A 以2cm/s 的速度向 B 爬行,同时另一小
虫由点 O 以3 cm/s 的速度沿 OC 行,则在几秒时两小
虫所在位置与点O组成的三角形的面积等于 450 cm2
O
A
B
C
O
A
B
C
O
A
B
C
O
A
B
C
O
A
B
C
O
A
B
C
O
A
B
C
O
A
B
C
O
A
B
C
6. 某公司实行年薪工资制,职工的年薪工资由基本工资、
工龄工资和岗位工资三项组成,具体规定如下:
项目 第一年的工资(万元) 一年后的计算方法
基本工资 2 每年增长率相同
工龄工资 0.08 每年增加0.08 万元
岗位工资 0.276 8 固定不变
(1) 设基本工资每年增长率为 x,用含的代数式表示第三
年的基本工资;
(2) 某人在公司工作了3 年,他这3 年拿到的工资和岗位
工资正好是这3 年基本工资总额的 18%,问基本工资每
年的增长率是多少
7. 在一次象棋比赛中,实行单循环赛制(即每个选手都与
其他选手比赛一局),每局赢者记 2 分,负者记0分,
如果平局,两个选手各记1分.今有 4个同学统计了比赛
中全部选手的得分总和,结果
分别为2 005,2004,2070,
2 008,经核实确定只有一位同
学统计正确,试计算这次比赛
中共有多少名选手参赛.
8. 一小艇顺流航行 24 km 到达目的地,然后逆流回到出
发地,航行时间共 6 h.已知水流速度是 3 km/h.求小艇
在静水中的速度.
9. 某商店以 2 400 元购进一种盒装茶叶,第一个月每盒
按进价增加 20% 作为售价售出 50 盒.第二个月每盒以
低于进价 5 元作为售价,售完余下的茶叶.全部售完后
共盈利 350 元,求每盒茶叶的进价.
10. 一商店用 1800 元买进玩具若干个,其中有 2个损坏
无法出售,剩余的每个以比进价多5 元的价格出售.若
剩余的全部卖完,则这批玩具共赚 400 元.问这批玩
具每个进价是多少元 共买进了多少个玩具
本课结束
第17章 一元二次方程
义务教育沪科版数学八年级下册
小结与复习
内容整理
一元二次方程
一元二次方程的解法
直接开平方
一元二次方程的应用
配方法
公式法
因式分解法
主要知识回顾
1. 一元二次方程
一般形式是 ax +bx+c=0,其中a≠0 .
只含有一个未知数,并且未知数的最高次数是 2 的整式方程,叫做一元二次方程.
2. 一元二次方程的解法有:
一元二次方程的解法 适用的方程类型
直接开平方法
配方法
公式法
因式分解
x2 + px + q = 0 ( p2 - 4q≥0)
(ax + m)2 = n (a ≠ 0,n≥0)
ax2 + bx +c = 0 (a ≠ 0,b2 - 4ac≥0)
(ax + m)(bx + n) = 0 (ab ≠ 0)
3. 一元二次方程根的判别式有什么作用
一元二次方程 ax +bx+c=0,辨别式为:
△=b2-4ac .
△ >0时,方程有两个不相等的实数根;
△ = 0时,方程有两个相等的实数根;
△ < 0时,方程无实数根 .
*4. 一元二次方程的根与系数有怎样的关系
设 x1,x2 是方程 ax +bx+c=0 的两个根,
x1 + x2 = -
x1 · x2 =
复习题
A组
1. 解下列方程:
(1) x2 = 64;
(2) x2 = 8;
x=±.
x = ± 8
即 x1 = 8,
x2 =- 8
x=±.
x = ±2
即x1 = 2,
x2 =- 2
(3) (3x+2)2 = 4(x-3)2;
(3x+2)2 -4(x-3)2=0
[3x+2+2(x-3)][3x+2-2(x-3)] =0
(5x-4)(x+8) =0
5x-4=0 或 x+8=0
x1=,x2=-8
(4) y2 -3y =0;
y (y -3) =0
y=0 或y -3 =0
解得:y1 = 0,
y2 =
(5) (2x +1)2 = 2x +1.
(2x +1)2 -2x +1=0
[(2x +1) -1](2x +1) =0
2x(2x+1) =0
2x=0或2x+1=0
解得: x1=0,x2=-
2. 用配方法解下列方程:
(1) x2-x-1 = 0;
(2) 3x2 =-1-5x ;
(3) 5y -84 +y2 =0;
(4) 2x2+x =3.
3. 用公式法解下列方程:
(1) x2+2 = 2x;
(2) 9x2 + 4 = 12x;
(3) (2x -1)2 -5 = x(x -5);
(4) y - = 1 .
4. 用适当方法解下列方程:
(1) x2 + 6x - 5 = 0;
(2) (x + 3)(x - 3) = 2;
(3) (t - )2 + 4t = 0;
(4) 3x(x - 1) = 2 - 2x.
5. 已知关于x的方程 2x2 - 5x + k = 0的一个根是 1.
(1) 求k的值;
(2) 解这个方程.
6. 设 x1,x2 是方程 2x2 +5x -7 =0 的两个根,不解方
程,求下列式子的值.
(1) x12 + x22 ;
(2) + .
7. 有一块长 25 cm宽 15 cm 的长方形硬纸板,如果在纸
板的四个角上各截去一个相同大小的小正方形,然后
把四边折起来,做成一个底面积为 231 cm2的无盖长
方体盒子.求截去的小正方形的边长.
8. 某商厦 10 月份的营业额是 50 万元,第四季度的营业
额是 182 万元问. 第四季度后两个月的月平均营业额
的增长率是多少
复习题
B组
1. 已知 y = x2 - 2x - 3.
(1) x 是什么数时,y = 0
1. 已知 y = x2 - 2x - 3.
(2) x 是什么数时,y = - 4
2. 有三个连续奇数,已知它们的平方和等于251,求这
三个数.
3. 已知:关于x的一元二次方程 (b - c)x2 + (c - a)x +(a-b) = 0 有两个相等的实数根. 求证:2b = a + c.
证明:因为方程有两个相等的实数根,
所以(c-a)2-4(b-c)(a-b) =0。
整理得(c+a-2b) =0,
所以2b=a+c。
4. 要建一个面积为 150 m2 的长方形养鸡场,为了节省
材料,养鸡场的一边利用原有的一道墙,另三边用铁
丝网围成,如果铁丝网的长为 35 m.
(1) 若墙足够长,则养鸡场的长与宽各为多少
设垂直于墙的边长为 x m,则平行于墙的边长为(35-2x)m,
依题意,得:x(35-2x) =150,
整理,得:2x2-35x+150=0,
解得: x1=7.5,x2=10,
∴35-2x=20或35-2x=15.
答:养鸡场的长为20m或15m,宽为7.5m或10m.
(2) 若给定墙长为 a m,则墙长 a 对题目的解是否有影响
当a < 15时,题目无解;
当15 ≤ a < 20时,题目只有一个解;
当a ≥ 20时,题目有两个解.
5. 如图,OA=OB=50cm,OC 是一条射线,OC ⊥AB,
一小虫由点 A 以2cm/s 的速度向 B 爬行,同时另一小
虫由点 O 以3 cm/s 的速度沿 OC 行,则在几秒时两小
虫所在位置与点O组成的三角形的面积等于 450 cm2
O
A
B
C
O
A
B
C
O
A
B
C
O
A
B
C
O
A
B
C
O
A
B
C
O
A
B
C
O
A
B
C
O
A
B
C
6. 某公司实行年薪工资制,职工的年薪工资由基本工资、
工龄工资和岗位工资三项组成,具体规定如下:
项目 第一年的工资(万元) 一年后的计算方法
基本工资 2 每年增长率相同
工龄工资 0.08 每年增加0.08 万元
岗位工资 0.276 8 固定不变
(1) 设基本工资每年增长率为 x,用含的代数式表示第三
年的基本工资;
(2) 某人在公司工作了3 年,他这3 年拿到的工资和岗位
工资正好是这3 年基本工资总额的 18%,问基本工资每
年的增长率是多少
7. 在一次象棋比赛中,实行单循环赛制(即每个选手都与
其他选手比赛一局),每局赢者记 2 分,负者记0分,
如果平局,两个选手各记1分.今有 4个同学统计了比赛
中全部选手的得分总和,结果
分别为2 005,2004,2070,
2 008,经核实确定只有一位同
学统计正确,试计算这次比赛
中共有多少名选手参赛.
8. 一小艇顺流航行 24 km 到达目的地,然后逆流回到出
发地,航行时间共 6 h.已知水流速度是 3 km/h.求小艇
在静水中的速度.
9. 某商店以 2 400 元购进一种盒装茶叶,第一个月每盒
按进价增加 20% 作为售价售出 50 盒.第二个月每盒以
低于进价 5 元作为售价,售完余下的茶叶.全部售完后
共盈利 350 元,求每盒茶叶的进价.
10. 一商店用 1800 元买进玩具若干个,其中有 2个损坏
无法出售,剩余的每个以比进价多5 元的价格出售.若
剩余的全部卖完,则这批玩具共赚 400 元.问这批玩
具每个进价是多少元 共买进了多少个玩具
本课结束
