第20章 数据的初步分析 小结与复习 -初中数学沪科版八年级下册课件(共84张PPT)
文档属性
| 名称 | 第20章 数据的初步分析 小结与复习 -初中数学沪科版八年级下册课件(共84张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 57.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-21 09:37:53 | ||
图片预览










文档简介
(共84张PPT)
第20章 数据的初步分析
义务教育沪科版数学八年级下册
小结与复习
内容整理
数据的初步分析
数据的频数分布
数据的集中趋势与离散程度
主要知识回顾
一、数据的集中趋势
平均数 定义 一组数据的平均值称为这组数据的平均数
算术平 均数 一般地,如果有 n 个数 x1,x2,…,xn,那么_____________________叫做这 n 个数的平均数
平均数 加权平 均数 一般求加权平均数,可统一用下面的公式:
______________________________________
____叫做这 n 个数据的加权平均数
中位数 定义 将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,那么处于________________就是这组数据的中位数;如果数据的个数是偶数,那么中间___________________就是这组数据的中位数
防错 提醒 确定中位数时,一定要注意先把整组数据按照由小到大(或由大到小)的顺序排列,再确定.
中间位置的数
两个数据的平均数
众 数 定义 一组数据中出现次数________的数据叫做这组数据的众数
防错 提醒 (1) 一组数据中众数不一定只有一个,还可能没有;
(2) 当一组数据中含极端值时,其平均数往往不能准确反映这组数据的集中趋势,应考虑用中位数或众数来分析
最多
二、数据的波动程度
表示波 动的量 定义 意义
方差 设有 n 个数据 x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是 (x1 - )2,(x2 - )2,…,(xn - )2,我们用它们的平均数,即用_________________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作 s2 方差越大,数据的波动越___,反之也成立
大
平均数
三、用样本估计总体
1.统计的基本思想:用样本的特征(平均数和方差)估
计总体的特征.
2.统计的决策依据:利用数据做决策时,要全面、多
角度地去分析已有数据,从数据的变化中发现它们
的规律和变化趋势,减少人为因素的影响.
复习题
A组
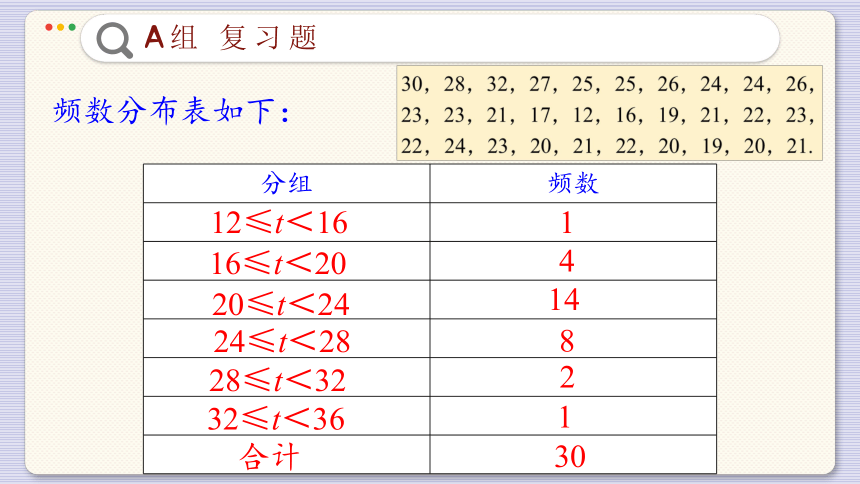
1. 下列数据为某城市2012 年 11 月份每天最高的气温
(单位:C):
30,28,32,27,25,25,26,24,24,26,
23,23,21,17,12,16,19,21,22,23,
22,24,23,20,21,22,20,19,20,21.
先适当分组,列出频数分布表,再绘制频数直方图.
频数分布表如下:
分组 频数
8
12≤t<16
16≤t<20
1
4
20≤t<24
14
24≤t<28
28≤t<32
2
32≤t<36
1
合计
30
频数分布直方图如下:
12 16 20 24 28 32 36
14
12
10
8
6
4
2
0
气温
天数
1
4
14
8
2
1
2. 如图是九年级 2 班学生的一次体检中每分钟心跳次数的频数直方图(次数均为
整数). 已知该班只有 5 位
学生的心跳每分钟 75 次,
请观察图后,指出下列说
法是否正确
(1) 数据 75 落在第 2小组;
(2)第4 小组的频率为 0.1;
由第2组的范围是69.5~79.5知数据75落在第2小组,故此说法正确;
第4小组的频率为
= 0.1,故此说法正确;
(3) 心跳为每分钟 75 次的人数占该班体检人数的.
心跳为每分钟75次的人数占该班体检人数的 = ,
故此说法正确.
3. 为了了解学校开展“孝敬父母,从家务事做起”活动的实际情况,该校抽取八年级50名学生,调查他们一周(按 7 天计算)家务所用时间(单位:h),得到一组数据,并绘制成下表,请根据该表完成下列各题:
(1) 填写频数分布表中未完成的部分;
频数分布表
分组 频数 频率
0.55~1.05 14 0.28
1.05~1.55 15 0.30
1.55~2.05 7 0.14
2.05~2.55 4 0.08
2.55~3.05 5 0.10
3.05~3.55 3 0.06
3.55~4.05 2 0.04
合计 50 1.00
(2) 由以上信息判断,每周做家务的时间不超过 1.5 h 的学生所占百分率是_______.
58%
4. 希望中学为了解九年级男生的身高情况,抽测了 50 名男生的身高(单位:m),数据如下:
身高/m 1.57 1.60 1.62 1.64 1.65 1.66 1.67 1.68 1.69
人数 1 1 1 3 3 3 2 4 6
身高/m 1.70 1.71 1.72 1.73 1.74 1.75 1.76 1.78 1.80
人数 7 7 2 3 2 1 2 1 1
(1) 若将数据分成6组,取组距为 0.04 m,试完成相应的频数分布表:
分组 1.565 ~ 1.605 1.605 ~ 1.645 1.645 ~ 1.685 1.685 ~ 1.725 1.725 ~ 1.765 1.765 ~ 1.805 合计
频数 2 4 12 22 8 2 50
(2) 画出频数直方图;
身高
(m)
人数(人)
1.565
1.605
1.645
1.685
1.725
1.765
1.805
24
20
16
12
8
4
0
2
4
12
22
8
2
(3) 根据样本数据,身高在 1.695 ~1.755 之间的男生所占的百分率为多少 如果该校九年级共有 450名男生,那么在 1.695~1.755 m之间的人数约有多少人
所占的百分率为:
×100%=44%
(3) 根据样本数据,身高在 1.695 ~1.755 之间的男生所占的百分率为多少 如果该校九年级共有 450名男生,那么在 1.695~1.755 m之间的人数约有多少人
人数约有:
450 ×44% =198(人)
5. 某校为推动信息技术的发展,举行了电脑设计作品比赛,各个班派学生代表参加现将所有比赛成绩(得分取整数,满分为 100 分)进行整理后分成五组,并绘制成如图所示的频数直方图,请根据统计图提供的信息,解答下列问题:
(1) 参加比赛的学生代表共有多少人
4+12+20+10+6=52(人)
(2) 80.5 ~90.5 分这个分数段的频数频率分别是多少
由图示知,80.5 ~90.5分这个分数段的频数是10.
频率是: = .
(3) 根据统计图,请你提出一个问题,并回答.
问题:若80.5分以上为优秀,问这次电脑设计作品比赛的优秀率约为多少?
× 100% ≈ 31%
6. 某邮局有 A,B,C,D 四名投递员,年终时按职业道德、工作态度、工作能力及工作实绩四个方面进行考核,每一项的满分均为 100 分,得分最高者为本年度先进工作者. 如果各方面的权数及四名投递员的得分如下:
考核项目 权数 投递员及得分
A B C D
职业道德 2 80 81 80 81
工作态度 2 85 82 78 80
工作能力 3 70 78 85 83
工作实绩 3 75 80 70 85
考核项目 权数 投递员及得分
A B C D
职业道德 2 80 81 80 81
工作态度 2 85 82 78 80
工作能力 3 70 78 85 83
工作实绩 3 75 80 70 85
问谁是本年度的先进工作者
A
考核项目 权数 投递员及得分
A B C D
职业道德 2 80 81 80 81
工作态度 2 85 82 78 80
工作能力 3 70 78 85 83
工作实绩 3 75 80 70 85
B
C
考核项目 权数 投递员及得分
A B C D
职业道德 2 80 81 80 81
工作态度 2 85 82 78 80
工作能力 3 70 78 85 83
工作实绩 3 75 80 70 85
D
∵ 78 <78.1 <80 <82.6,
∴ D为本年度先进工作者.
7. 华东地区主要城市某天的最低气温情况如图所示.
求这些城市该天最低气温的平均数、中位数和众数.
平均数: =
≈1.6℃
共有18个城市,气温从小到大排列后处在第9、10位的两个数都是1℃,故中位数是1℃.
最低气温为1℃的城市最多为9个,因此这些城市该天最低气温的众数是1℃;
答:些城市该天最低气温的平均数为1.6℃,中位数是1℃ ,众数是1℃.
8. 某班学生百米跑测试成绩如下表所示:
成绩/s 15 15.5 16 16.5 17 17.5 18
学生人数 2 3 6 21 11 4 3
求测试成绩的中位数、众数和平均数(精确到 0.1s).
将这些成绩按从小到大的顺序排列,处于最中间的两个成绩为16.5和16.5,所以测试成绩的中位数为 16.5s .
成绩/s 15 15.5 16 16.5 17 17.5 18
学生人数 2 3 6 21 11 4 3
测试成绩中出现次数最多的成绩是16.5,所以测试成绩的众数为16.5s.
平均数为:
=16.5s
9. 甲、乙两台机床同时生产一种零件,在 10 天中,两
台机床每天出的次品数分别是:
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
分别计算两组数据的平均数和方差,并说明哪台机床在 10 天中出的次品数波动较大.
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
==1.5,
==1.2.
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
S甲2 =[(0-1.5) +(1-1.5) +(0-1.5) +(2 - 1.5) + (2 - 1.5) +(0 - 1.5) +(3 - 1.5) + (1 - 1.5) +(2 - 1.5) + (4 - 1.5) = 1.65.
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
S乙2 =[(2-1.2) +(3-1.2) +(1-1.2) +(1 - 1.2) + (0- 1.2) +(2 - 1.2) +(1 - 1.2) + (1 - 1.2) +(0 - 1.2) + (1 - 1.2) = 0.76.
∵ S甲2 = 1.65 > 0.76 = S乙2 ,
∴说明甲机床在10天内出现次品的波动较大.
10.甲、乙两台包装机同时包装质量为 200 g 的糖果,从
中分别抽出若干袋,测得其质量(单位:g)如下:
甲:203,204,202,196,199,201,205,197,
202,199;
乙:201,200,208,210,209,200,193,194.
(1) 分别计算两组数据的平均数和方差;
=(203 + 204 + 202 + 196 + 199+ 201+20+197+202+199)÷10 = 200.8
=(201+200+208+210+209+200+193+194)÷8=201.875;
(1) 分别计算两组数据的平均数和方差;
S甲2=[(203-200.8)2+(204-200.8)2+···+(199-200.8)2= 7.96,
S乙2 =(201-201.875)2+(200-201.875)2+··· +(194 - 201.875)2 = 20.42.
(2) 从计算结果看,哪台包装机包装的糖果的质量比
较稳定
∵S乙2 > S甲2
∴甲包装机包装10袋糖果的质量比较稳定.
11. 要从甲、乙两位车工中选拔一名参加技术比赛. 现从他们加工的零件中各抽取 5 个零件进行检验,测得它们的直径(单位:m)分别为:
甲:15.05,15.02,14.97,14.96,15.00;
乙:15.00,15.01,15.02,14.97,15.00.
问哪位车工的技术发挥较稳定
甲:15.05,15.02,14.97,14.96,15.00;
乙:15.00,15.01,15.02,14.97,15.00.
= (15.05 + 15.02 +14.97 + 14.96+ 15.00) ÷ 5 = 15.00,
= (15.00 + 15.01 + 15.02 + 14.97 + 15.00)÷5 = 15.00;
甲:15.05,15.02,14.97,14.96,15.00;
乙:15.00,15.01,15.02,14.97,15.00.
S甲2 =[(15.05-15.00)2+(15.02-15.00)2+···+(15.00-15.00) ]÷5 = 0.00108,
S乙2 =(15.05-15.00) +(15.02-15.00)2+···+(15.00-15.00)2÷5 = 0.0014,
∵ S甲2 < S乙2,
∴甲车工的技术发挥较稳定.
12. 某粮店购进东北大米 1000 袋,为了检验每袋大米的质量,从中任意抽取 10 袋大米,称得质量(单位:kg)如下:
10,10.2,9.9,10,9.9,9.9,10.1,10,10.1,10.
请你估计这批大米的质量.
=10× (10+10.2+···+10) = 10.01(kg).
所以估计这批大米的质量约为
10.01 × 1000 = 10010(kg)。
13. 某鱼塘放养鱼苗 10 万条,根据这几年经验知道,鱼苗成活率为 95%. 一段时间后,准备将鱼打捞出售. 第一次网出 40 条,称得平均鱼重 2.5 kg;第二次网出25条,称得平均鱼重 2.2 g;第三次网出 35 条,称得平均鱼重2.8 kg,请你估计鱼塘中鱼的总质量为多少千克
由题意可得:
(40×2.5+25×2.2+35×2.8)÷(40+25+35)=2.53(千克),
故10万×95%×2.53 = 240350(千克),
答:鱼塘中的鱼总质量大约是240350千克.
14. 从某灯泡厂生产的一批灯泡中随机地抽取 10 只进行寿命测试,得到数据(单位:h)如下:
1 458,1 395,1 562,1 614,1 351,
1 490,1 478,1 382,1 536,1 496.
试估计这批灯泡的平均寿命及寿命的方差.
1 458,1 395,1 562,1 614,1 351,
1 490,1 478,1 382,1 536,1 496.
= (1458+1395+1562 + 1614+1351+ 1490 + 1478 + 1382 + 1536 + 1496) = 1476.2,
方差= [(1458-1476.2)2+(1395-1476.2) +···+(1496-1476.2)2] = 6198.56.
复习题
B组
1.无核柑橘是皖西南山区特产. 小明家有一块成龄无核柑橘园,去年采摘时,小明利用统计知识. 对柑橘的等级和产量进行了测算:他随机选择了若干棵柑橘树,从中共摘得 240个柑橘,并对这些柑橘的直径进行了测量和统计,绘制出如图(1)所示的频数直方图. 已知一级鲜柑橘的直径在 5.5~7.5 cm 之间.
(1) 估计柑橘园中一级柑橘所占的比例是多少;
估计柑橘园中一级柑
橘所占的比例是
×100%=45%
因此估计柑橘园中一级柑橘所占的比例是45%
(2) 由于受储存季节的变化等影响,柑橘的售价会随时间的变化而变化,每千克一级柑橘的月平均售价变化情况如图(2). 若小明家去年共摘得一级柑橘4 000 kg. 现请你利用图象提供的信息,计算出小明家的一级橘在 4月份出售时,一共能卖多少钱 (不考虑其他因素对柑橘质量的影响)
小明家的一级柑橘在4月份出售时,一共能卖
4000×[1.2+ (1.6-1.2)÷4×3=6000(元)
因此小明家的一级柑橘在4月份出售时,一共能卖6000元.
2. 某风景区对 5 个旅游景点的门票价格进行了调整. 据统计,调价前后各景点的客人数基本不变. 有关数据如下表:
景点 A B C D E
原价/元 10 10 15 20 25
现价/元 5 5 15 25 30
日平均游客人数 1000 1000 2000 3000 2000
风景区管理部门:调价前后这 5 个景点门票的平均价格
不变. 因而,就总体而言,风景区在
门票价格调整中没有获益.
游客:调整门票价格后风景区的平均日收入相对于调价
前实际增加了 9.4%因此调价对风景区有利.
请你分析他们的说法谁符合实际.
游客的说法符合实际。理由如下:
调价前风景区平均日收入为:
(10×1+10×1+15×2+20×3+25 ×2)×1000 ≈160000(元)
调价后风景区平均日收入为:
(5×1+5×1+15×2+25×3+30×2) ×1000 = 175000(元)
调价后风景区平均日收入比调价前风景区平均日收入的增长率为:× 100% ≈ 9.4%
因此游客的说法符合实际.
3. 公交6 路汽车总站设在一个新开发的居民小区附近,这个小区居民出行主要选乘6 路车为了了解在 7∶00 至8∶00 这个高峰时段内乘该路车的人数,公交公司抽查了 10 个班次的乘车人数,结果如下:
25,28,34,36,35,36,32,30,28,26.
25,28,34,36,35,36,32,30,28,26.
(1) 计算这 10 个班次乘该路车人数的平均数;
这10个班次乘车人数的平均数为
×(25+ 28+ 34+36 + 35+36+32+30+28+26) = 31(人);
(2) 如果在高峰时段从总站发车 20 个班次估计在高峰时段乘该路车的人数.
20 × 31 = 620(人)。
答:估计在高峰时段乘该路车的人数有620人。
4. 甲、乙两人在相同的条件下各射靶 10 次,每次射靶的成绩如下:
甲:9,5,7,8,7,6,8,6,7,7;
乙:2,4,6,8,7,7,8,9,9,10.
(1) 填写下表:
平均数 中位数 方差 命中9环以上的次数
甲 7 7 1.2 0
乙 7 7.5 5.4 1
平均数 中位数 方差 命中9环以上的次数
甲 7 7 1.2 0
乙 7 7.5 5.4 1
(2) 请从下面 4 个不同的角度对这次测试结果进行分析:
①平均数和方差相结合,分析谁的成绩稳定;
方差反映了一组数据的波动大小,方差越大,波动性越大.甲的成绩稳定;
平均数 中位数 方差 命中9环以上的次数
甲 7 7 1.2 0
乙 7 7.5 5.4 1
②平均数和中位数相结合,分析谁的成绩好些;
平均数和中位数相结合,乙的成绩好些;
平均数 中位数 方差 命中9环以上的次数
甲 7 7 1.2 0
乙 7 7.5 5.4 1
③平均数和命中9环以上的次数相结合,分析谁的成绩好些;
平均数与命中9环以上的次数相结合,乙的成绩好些;
④ 作折线统计图,从折线统计图上两人射击命中环数的走势分析,谁更有潜力.
乙有潜力,因为乙后来逐渐稳定,成绩越来越好.
5. 某市林业局于 2005 年对直接从原产地引进的绒毛白蜡树种进行育苗造林,经过3年育苗试验、6 年造林试验获得成功.
苗木高、径生长量表
该林业局农艺师根据此表作出分析:“从苗木高、径生长情况看苗木逐年出现分化,且分化程度不断增加,说明播种苗有再选优的必要性和可能性.”
(1) 比较同一苗龄两个苗圃苗木高、径的平均数;
由表格中的信息可知:同一苗龄乙苗圃的高,径的平均数比甲苗圃的高,径的平均数值要大.
(2) 比较同一苗龄两个苗圃苗木高、径的年平均生长值;
由表格中的信息可知:同一苗龄乙苗圃的高,径年平均生长值比甲苗圃的高,径的值要大.
(3)同一苗龄两个苗圃苗木高、径的平均数、方差所反映苗木的差异;
由表格中的信息可知:
同一苗龄乙苗圃苗木高、径的平均数比甲苗圃苗木高、径的平均数要大,2龄苗,3龄苗乙苗圃苗木高、径的方差比甲苗圃苗木高、径的方差要小.
(4) 决定优选哪个苗圃的树苗.
由表格中的信息可知:选乙苗圃苗木比较好.
复习题
C组
某村为了对甲、乙两名村干部进行年度考核,召开了一次述职答辩及民主测评会. 乡政府派出 A,B,C,D,E 五位评委对“述职答辩”进行评价;并从村里选出 20名村民代表参加民主测评. 结果如表所示:
规定:述职答辩得分“按去掉一个最高分和一个最低分再算平均分”的方法确定:
综合得分 =述职答辩得分×(1-a)+民主测评得分×a (0.5 ≤ a≤0.8).
民主测评得分 = “优秀”票数×5+“良好”票数×3+“一般”票数×1;
(1)当a =0.6时,甲和乙的综合得分分别是多少
甲的述职答辩得分 =92(分)
乙的述职答辩得分 =89(分)
甲民主测评得分=12 ×5 +6 ×3 +2 ×1 =80(分)
乙民主测评得分=13 ×5 +5 ×3 +2 ×1 =82(分)
甲的综合得分=92×(1-a)+80×a=92-12a (分),
当a = 0.6 时,
甲的综合得分= 92 - 12×0.6 =84.8 (分);
乙的综合得分= 89 - 7×0.6=84.8 (分).
乙的综合得分=89×(1-a)+82×a=89-7a (分),
(2)甲的综合得分高时,a 在什么范围 乙的综合得分高时,a 又在什么范围
当甲的综合得分高时,有92 - 12a > 89 - 7a,
解得:a<0.6,
所以,当0.5<a<0.6时,甲的综合得分高;
当0.6 <a<0.8时,乙的综合得分高.
本课结束
第20章 数据的初步分析
义务教育沪科版数学八年级下册
小结与复习
内容整理
数据的初步分析
数据的频数分布
数据的集中趋势与离散程度
主要知识回顾
一、数据的集中趋势
平均数 定义 一组数据的平均值称为这组数据的平均数
算术平 均数 一般地,如果有 n 个数 x1,x2,…,xn,那么_____________________叫做这 n 个数的平均数
平均数 加权平 均数 一般求加权平均数,可统一用下面的公式:
______________________________________
____叫做这 n 个数据的加权平均数
中位数 定义 将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,那么处于________________就是这组数据的中位数;如果数据的个数是偶数,那么中间___________________就是这组数据的中位数
防错 提醒 确定中位数时,一定要注意先把整组数据按照由小到大(或由大到小)的顺序排列,再确定.
中间位置的数
两个数据的平均数
众 数 定义 一组数据中出现次数________的数据叫做这组数据的众数
防错 提醒 (1) 一组数据中众数不一定只有一个,还可能没有;
(2) 当一组数据中含极端值时,其平均数往往不能准确反映这组数据的集中趋势,应考虑用中位数或众数来分析
最多
二、数据的波动程度
表示波 动的量 定义 意义
方差 设有 n 个数据 x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是 (x1 - )2,(x2 - )2,…,(xn - )2,我们用它们的平均数,即用_________________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作 s2 方差越大,数据的波动越___,反之也成立
大
平均数
三、用样本估计总体
1.统计的基本思想:用样本的特征(平均数和方差)估
计总体的特征.
2.统计的决策依据:利用数据做决策时,要全面、多
角度地去分析已有数据,从数据的变化中发现它们
的规律和变化趋势,减少人为因素的影响.
复习题
A组
1. 下列数据为某城市2012 年 11 月份每天最高的气温
(单位:C):
30,28,32,27,25,25,26,24,24,26,
23,23,21,17,12,16,19,21,22,23,
22,24,23,20,21,22,20,19,20,21.
先适当分组,列出频数分布表,再绘制频数直方图.
频数分布表如下:
分组 频数
8
12≤t<16
16≤t<20
1
4
20≤t<24
14
24≤t<28
28≤t<32
2
32≤t<36
1
合计
30
频数分布直方图如下:
12 16 20 24 28 32 36
14
12
10
8
6
4
2
0
气温
天数
1
4
14
8
2
1
2. 如图是九年级 2 班学生的一次体检中每分钟心跳次数的频数直方图(次数均为
整数). 已知该班只有 5 位
学生的心跳每分钟 75 次,
请观察图后,指出下列说
法是否正确
(1) 数据 75 落在第 2小组;
(2)第4 小组的频率为 0.1;
由第2组的范围是69.5~79.5知数据75落在第2小组,故此说法正确;
第4小组的频率为
= 0.1,故此说法正确;
(3) 心跳为每分钟 75 次的人数占该班体检人数的.
心跳为每分钟75次的人数占该班体检人数的 = ,
故此说法正确.
3. 为了了解学校开展“孝敬父母,从家务事做起”活动的实际情况,该校抽取八年级50名学生,调查他们一周(按 7 天计算)家务所用时间(单位:h),得到一组数据,并绘制成下表,请根据该表完成下列各题:
(1) 填写频数分布表中未完成的部分;
频数分布表
分组 频数 频率
0.55~1.05 14 0.28
1.05~1.55 15 0.30
1.55~2.05 7 0.14
2.05~2.55 4 0.08
2.55~3.05 5 0.10
3.05~3.55 3 0.06
3.55~4.05 2 0.04
合计 50 1.00
(2) 由以上信息判断,每周做家务的时间不超过 1.5 h 的学生所占百分率是_______.
58%
4. 希望中学为了解九年级男生的身高情况,抽测了 50 名男生的身高(单位:m),数据如下:
身高/m 1.57 1.60 1.62 1.64 1.65 1.66 1.67 1.68 1.69
人数 1 1 1 3 3 3 2 4 6
身高/m 1.70 1.71 1.72 1.73 1.74 1.75 1.76 1.78 1.80
人数 7 7 2 3 2 1 2 1 1
(1) 若将数据分成6组,取组距为 0.04 m,试完成相应的频数分布表:
分组 1.565 ~ 1.605 1.605 ~ 1.645 1.645 ~ 1.685 1.685 ~ 1.725 1.725 ~ 1.765 1.765 ~ 1.805 合计
频数 2 4 12 22 8 2 50
(2) 画出频数直方图;
身高
(m)
人数(人)
1.565
1.605
1.645
1.685
1.725
1.765
1.805
24
20
16
12
8
4
0
2
4
12
22
8
2
(3) 根据样本数据,身高在 1.695 ~1.755 之间的男生所占的百分率为多少 如果该校九年级共有 450名男生,那么在 1.695~1.755 m之间的人数约有多少人
所占的百分率为:
×100%=44%
(3) 根据样本数据,身高在 1.695 ~1.755 之间的男生所占的百分率为多少 如果该校九年级共有 450名男生,那么在 1.695~1.755 m之间的人数约有多少人
人数约有:
450 ×44% =198(人)
5. 某校为推动信息技术的发展,举行了电脑设计作品比赛,各个班派学生代表参加现将所有比赛成绩(得分取整数,满分为 100 分)进行整理后分成五组,并绘制成如图所示的频数直方图,请根据统计图提供的信息,解答下列问题:
(1) 参加比赛的学生代表共有多少人
4+12+20+10+6=52(人)
(2) 80.5 ~90.5 分这个分数段的频数频率分别是多少
由图示知,80.5 ~90.5分这个分数段的频数是10.
频率是: = .
(3) 根据统计图,请你提出一个问题,并回答.
问题:若80.5分以上为优秀,问这次电脑设计作品比赛的优秀率约为多少?
× 100% ≈ 31%
6. 某邮局有 A,B,C,D 四名投递员,年终时按职业道德、工作态度、工作能力及工作实绩四个方面进行考核,每一项的满分均为 100 分,得分最高者为本年度先进工作者. 如果各方面的权数及四名投递员的得分如下:
考核项目 权数 投递员及得分
A B C D
职业道德 2 80 81 80 81
工作态度 2 85 82 78 80
工作能力 3 70 78 85 83
工作实绩 3 75 80 70 85
考核项目 权数 投递员及得分
A B C D
职业道德 2 80 81 80 81
工作态度 2 85 82 78 80
工作能力 3 70 78 85 83
工作实绩 3 75 80 70 85
问谁是本年度的先进工作者
A
考核项目 权数 投递员及得分
A B C D
职业道德 2 80 81 80 81
工作态度 2 85 82 78 80
工作能力 3 70 78 85 83
工作实绩 3 75 80 70 85
B
C
考核项目 权数 投递员及得分
A B C D
职业道德 2 80 81 80 81
工作态度 2 85 82 78 80
工作能力 3 70 78 85 83
工作实绩 3 75 80 70 85
D
∵ 78 <78.1 <80 <82.6,
∴ D为本年度先进工作者.
7. 华东地区主要城市某天的最低气温情况如图所示.
求这些城市该天最低气温的平均数、中位数和众数.
平均数: =
≈1.6℃
共有18个城市,气温从小到大排列后处在第9、10位的两个数都是1℃,故中位数是1℃.
最低气温为1℃的城市最多为9个,因此这些城市该天最低气温的众数是1℃;
答:些城市该天最低气温的平均数为1.6℃,中位数是1℃ ,众数是1℃.
8. 某班学生百米跑测试成绩如下表所示:
成绩/s 15 15.5 16 16.5 17 17.5 18
学生人数 2 3 6 21 11 4 3
求测试成绩的中位数、众数和平均数(精确到 0.1s).
将这些成绩按从小到大的顺序排列,处于最中间的两个成绩为16.5和16.5,所以测试成绩的中位数为 16.5s .
成绩/s 15 15.5 16 16.5 17 17.5 18
学生人数 2 3 6 21 11 4 3
测试成绩中出现次数最多的成绩是16.5,所以测试成绩的众数为16.5s.
平均数为:
=16.5s
9. 甲、乙两台机床同时生产一种零件,在 10 天中,两
台机床每天出的次品数分别是:
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
分别计算两组数据的平均数和方差,并说明哪台机床在 10 天中出的次品数波动较大.
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
==1.5,
==1.2.
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
S甲2 =[(0-1.5) +(1-1.5) +(0-1.5) +(2 - 1.5) + (2 - 1.5) +(0 - 1.5) +(3 - 1.5) + (1 - 1.5) +(2 - 1.5) + (4 - 1.5) = 1.65.
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
S乙2 =[(2-1.2) +(3-1.2) +(1-1.2) +(1 - 1.2) + (0- 1.2) +(2 - 1.2) +(1 - 1.2) + (1 - 1.2) +(0 - 1.2) + (1 - 1.2) = 0.76.
∵ S甲2 = 1.65 > 0.76 = S乙2 ,
∴说明甲机床在10天内出现次品的波动较大.
10.甲、乙两台包装机同时包装质量为 200 g 的糖果,从
中分别抽出若干袋,测得其质量(单位:g)如下:
甲:203,204,202,196,199,201,205,197,
202,199;
乙:201,200,208,210,209,200,193,194.
(1) 分别计算两组数据的平均数和方差;
=(203 + 204 + 202 + 196 + 199+ 201+20+197+202+199)÷10 = 200.8
=(201+200+208+210+209+200+193+194)÷8=201.875;
(1) 分别计算两组数据的平均数和方差;
S甲2=[(203-200.8)2+(204-200.8)2+···+(199-200.8)2= 7.96,
S乙2 =(201-201.875)2+(200-201.875)2+··· +(194 - 201.875)2 = 20.42.
(2) 从计算结果看,哪台包装机包装的糖果的质量比
较稳定
∵S乙2 > S甲2
∴甲包装机包装10袋糖果的质量比较稳定.
11. 要从甲、乙两位车工中选拔一名参加技术比赛. 现从他们加工的零件中各抽取 5 个零件进行检验,测得它们的直径(单位:m)分别为:
甲:15.05,15.02,14.97,14.96,15.00;
乙:15.00,15.01,15.02,14.97,15.00.
问哪位车工的技术发挥较稳定
甲:15.05,15.02,14.97,14.96,15.00;
乙:15.00,15.01,15.02,14.97,15.00.
= (15.05 + 15.02 +14.97 + 14.96+ 15.00) ÷ 5 = 15.00,
= (15.00 + 15.01 + 15.02 + 14.97 + 15.00)÷5 = 15.00;
甲:15.05,15.02,14.97,14.96,15.00;
乙:15.00,15.01,15.02,14.97,15.00.
S甲2 =[(15.05-15.00)2+(15.02-15.00)2+···+(15.00-15.00) ]÷5 = 0.00108,
S乙2 =(15.05-15.00) +(15.02-15.00)2+···+(15.00-15.00)2÷5 = 0.0014,
∵ S甲2 < S乙2,
∴甲车工的技术发挥较稳定.
12. 某粮店购进东北大米 1000 袋,为了检验每袋大米的质量,从中任意抽取 10 袋大米,称得质量(单位:kg)如下:
10,10.2,9.9,10,9.9,9.9,10.1,10,10.1,10.
请你估计这批大米的质量.
=10× (10+10.2+···+10) = 10.01(kg).
所以估计这批大米的质量约为
10.01 × 1000 = 10010(kg)。
13. 某鱼塘放养鱼苗 10 万条,根据这几年经验知道,鱼苗成活率为 95%. 一段时间后,准备将鱼打捞出售. 第一次网出 40 条,称得平均鱼重 2.5 kg;第二次网出25条,称得平均鱼重 2.2 g;第三次网出 35 条,称得平均鱼重2.8 kg,请你估计鱼塘中鱼的总质量为多少千克
由题意可得:
(40×2.5+25×2.2+35×2.8)÷(40+25+35)=2.53(千克),
故10万×95%×2.53 = 240350(千克),
答:鱼塘中的鱼总质量大约是240350千克.
14. 从某灯泡厂生产的一批灯泡中随机地抽取 10 只进行寿命测试,得到数据(单位:h)如下:
1 458,1 395,1 562,1 614,1 351,
1 490,1 478,1 382,1 536,1 496.
试估计这批灯泡的平均寿命及寿命的方差.
1 458,1 395,1 562,1 614,1 351,
1 490,1 478,1 382,1 536,1 496.
= (1458+1395+1562 + 1614+1351+ 1490 + 1478 + 1382 + 1536 + 1496) = 1476.2,
方差= [(1458-1476.2)2+(1395-1476.2) +···+(1496-1476.2)2] = 6198.56.
复习题
B组
1.无核柑橘是皖西南山区特产. 小明家有一块成龄无核柑橘园,去年采摘时,小明利用统计知识. 对柑橘的等级和产量进行了测算:他随机选择了若干棵柑橘树,从中共摘得 240个柑橘,并对这些柑橘的直径进行了测量和统计,绘制出如图(1)所示的频数直方图. 已知一级鲜柑橘的直径在 5.5~7.5 cm 之间.
(1) 估计柑橘园中一级柑橘所占的比例是多少;
估计柑橘园中一级柑
橘所占的比例是
×100%=45%
因此估计柑橘园中一级柑橘所占的比例是45%
(2) 由于受储存季节的变化等影响,柑橘的售价会随时间的变化而变化,每千克一级柑橘的月平均售价变化情况如图(2). 若小明家去年共摘得一级柑橘4 000 kg. 现请你利用图象提供的信息,计算出小明家的一级橘在 4月份出售时,一共能卖多少钱 (不考虑其他因素对柑橘质量的影响)
小明家的一级柑橘在4月份出售时,一共能卖
4000×[1.2+ (1.6-1.2)÷4×3=6000(元)
因此小明家的一级柑橘在4月份出售时,一共能卖6000元.
2. 某风景区对 5 个旅游景点的门票价格进行了调整. 据统计,调价前后各景点的客人数基本不变. 有关数据如下表:
景点 A B C D E
原价/元 10 10 15 20 25
现价/元 5 5 15 25 30
日平均游客人数 1000 1000 2000 3000 2000
风景区管理部门:调价前后这 5 个景点门票的平均价格
不变. 因而,就总体而言,风景区在
门票价格调整中没有获益.
游客:调整门票价格后风景区的平均日收入相对于调价
前实际增加了 9.4%因此调价对风景区有利.
请你分析他们的说法谁符合实际.
游客的说法符合实际。理由如下:
调价前风景区平均日收入为:
(10×1+10×1+15×2+20×3+25 ×2)×1000 ≈160000(元)
调价后风景区平均日收入为:
(5×1+5×1+15×2+25×3+30×2) ×1000 = 175000(元)
调价后风景区平均日收入比调价前风景区平均日收入的增长率为:× 100% ≈ 9.4%
因此游客的说法符合实际.
3. 公交6 路汽车总站设在一个新开发的居民小区附近,这个小区居民出行主要选乘6 路车为了了解在 7∶00 至8∶00 这个高峰时段内乘该路车的人数,公交公司抽查了 10 个班次的乘车人数,结果如下:
25,28,34,36,35,36,32,30,28,26.
25,28,34,36,35,36,32,30,28,26.
(1) 计算这 10 个班次乘该路车人数的平均数;
这10个班次乘车人数的平均数为
×(25+ 28+ 34+36 + 35+36+32+30+28+26) = 31(人);
(2) 如果在高峰时段从总站发车 20 个班次估计在高峰时段乘该路车的人数.
20 × 31 = 620(人)。
答:估计在高峰时段乘该路车的人数有620人。
4. 甲、乙两人在相同的条件下各射靶 10 次,每次射靶的成绩如下:
甲:9,5,7,8,7,6,8,6,7,7;
乙:2,4,6,8,7,7,8,9,9,10.
(1) 填写下表:
平均数 中位数 方差 命中9环以上的次数
甲 7 7 1.2 0
乙 7 7.5 5.4 1
平均数 中位数 方差 命中9环以上的次数
甲 7 7 1.2 0
乙 7 7.5 5.4 1
(2) 请从下面 4 个不同的角度对这次测试结果进行分析:
①平均数和方差相结合,分析谁的成绩稳定;
方差反映了一组数据的波动大小,方差越大,波动性越大.甲的成绩稳定;
平均数 中位数 方差 命中9环以上的次数
甲 7 7 1.2 0
乙 7 7.5 5.4 1
②平均数和中位数相结合,分析谁的成绩好些;
平均数和中位数相结合,乙的成绩好些;
平均数 中位数 方差 命中9环以上的次数
甲 7 7 1.2 0
乙 7 7.5 5.4 1
③平均数和命中9环以上的次数相结合,分析谁的成绩好些;
平均数与命中9环以上的次数相结合,乙的成绩好些;
④ 作折线统计图,从折线统计图上两人射击命中环数的走势分析,谁更有潜力.
乙有潜力,因为乙后来逐渐稳定,成绩越来越好.
5. 某市林业局于 2005 年对直接从原产地引进的绒毛白蜡树种进行育苗造林,经过3年育苗试验、6 年造林试验获得成功.
苗木高、径生长量表
该林业局农艺师根据此表作出分析:“从苗木高、径生长情况看苗木逐年出现分化,且分化程度不断增加,说明播种苗有再选优的必要性和可能性.”
(1) 比较同一苗龄两个苗圃苗木高、径的平均数;
由表格中的信息可知:同一苗龄乙苗圃的高,径的平均数比甲苗圃的高,径的平均数值要大.
(2) 比较同一苗龄两个苗圃苗木高、径的年平均生长值;
由表格中的信息可知:同一苗龄乙苗圃的高,径年平均生长值比甲苗圃的高,径的值要大.
(3)同一苗龄两个苗圃苗木高、径的平均数、方差所反映苗木的差异;
由表格中的信息可知:
同一苗龄乙苗圃苗木高、径的平均数比甲苗圃苗木高、径的平均数要大,2龄苗,3龄苗乙苗圃苗木高、径的方差比甲苗圃苗木高、径的方差要小.
(4) 决定优选哪个苗圃的树苗.
由表格中的信息可知:选乙苗圃苗木比较好.
复习题
C组
某村为了对甲、乙两名村干部进行年度考核,召开了一次述职答辩及民主测评会. 乡政府派出 A,B,C,D,E 五位评委对“述职答辩”进行评价;并从村里选出 20名村民代表参加民主测评. 结果如表所示:
规定:述职答辩得分“按去掉一个最高分和一个最低分再算平均分”的方法确定:
综合得分 =述职答辩得分×(1-a)+民主测评得分×a (0.5 ≤ a≤0.8).
民主测评得分 = “优秀”票数×5+“良好”票数×3+“一般”票数×1;
(1)当a =0.6时,甲和乙的综合得分分别是多少
甲的述职答辩得分 =92(分)
乙的述职答辩得分 =89(分)
甲民主测评得分=12 ×5 +6 ×3 +2 ×1 =80(分)
乙民主测评得分=13 ×5 +5 ×3 +2 ×1 =82(分)
甲的综合得分=92×(1-a)+80×a=92-12a (分),
当a = 0.6 时,
甲的综合得分= 92 - 12×0.6 =84.8 (分);
乙的综合得分= 89 - 7×0.6=84.8 (分).
乙的综合得分=89×(1-a)+82×a=89-7a (分),
(2)甲的综合得分高时,a 在什么范围 乙的综合得分高时,a 又在什么范围
当甲的综合得分高时,有92 - 12a > 89 - 7a,
解得:a<0.6,
所以,当0.5<a<0.6时,甲的综合得分高;
当0.6 <a<0.8时,乙的综合得分高.
本课结束
