苏教版数学五年级下册 第六单元 圆-练习十四课件(共18张PPT)
文档属性
| 名称 | 苏教版数学五年级下册 第六单元 圆-练习十四课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-20 09:29:10 | ||
图片预览






文档简介
(共18张PPT)
五年级数学下册教学课件(苏教版)
第六单元 圆
练习十四
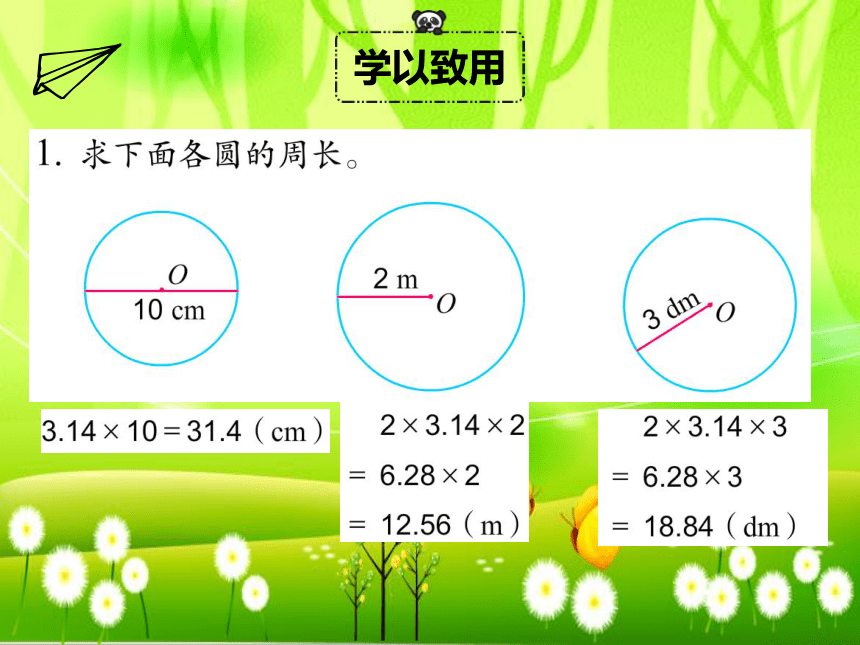
学以致用
01
学以致用
学以致用
学以致用
学以致用
学以致用
学以致用
0.5 分米
1.5 厘米
3 米
学以致用
7.滚铁环是一种有趣的儿童游戏。如果用一根长90厘米的铁片弯成一个圆形铁环,这个铁环的半径大约是多少厘米 (得数保留整数)
学以致用
用一根绳子绕这棵树的树干,量得10圈的绳长是12.56米。这棵树树干横截面的直径大约是多少厘米?
12.56÷10÷3.14
=1.256÷3.14
=0.4(米)=40(厘米)
答:这棵树树干横截面的直径大约是40厘米。
学以致用
9.圆形拱门的高度要在2.4~2.7米之间才符合标准。一个圆形拱门门框的周长大约是7.85米。它的高度符合标准吗?
2.7>
学以致用
学以致用
人类对圆周率的研究历史非常久远。 在古代, 人们大都认为圆的周长是直径的 3 倍, 我国古代的数学著作《周髀算经》中就有“周三径一”的记载。古希腊数学家阿基米德发现, 当正多边形的边数增加时, 它的形状就越来越接近圆。 他依据这个想法求出圆周率介于 和 之间。
学以致用
我国魏晋时期数学家刘徽采用“割圆术” 来求圆的周长的近似值。 他从圆的内接正六边形算起, 逐渐把边数加倍, 正十二边形,正二十四边形……求得圆周率的近似值是 3.14。
学以致用
大约 1500 年前, 我国南北朝科学家祖冲之使用刘徽的方法算出圆周率 π 大约在 3.1415926 和 3.1415927 之间, 成为世界上第一个把圆周率的值精确到小数点后 7 位的人。 他还发现一个与 π 值非常接近的分数 (约等于 3.1415929), 这一研究成果比国外数学家早了 1000 多年。
随着数学的发展, 特别是计算机的问世, 圆周率的精确度被算得越来越高。现在,人们已经能够把圆周率精确到小数点后数万亿位。
课后作业
02
完成教材课后习题及练习册同步练习。
课后作业
感 谢 观 看
五年级数学下册教学课件(苏教版)
第六单元 圆
练习十四
学以致用
01
学以致用
学以致用
学以致用
学以致用
学以致用
学以致用
0.5 分米
1.5 厘米
3 米
学以致用
7.滚铁环是一种有趣的儿童游戏。如果用一根长90厘米的铁片弯成一个圆形铁环,这个铁环的半径大约是多少厘米 (得数保留整数)
学以致用
用一根绳子绕这棵树的树干,量得10圈的绳长是12.56米。这棵树树干横截面的直径大约是多少厘米?
12.56÷10÷3.14
=1.256÷3.14
=0.4(米)=40(厘米)
答:这棵树树干横截面的直径大约是40厘米。
学以致用
9.圆形拱门的高度要在2.4~2.7米之间才符合标准。一个圆形拱门门框的周长大约是7.85米。它的高度符合标准吗?
2.7>
学以致用
学以致用
人类对圆周率的研究历史非常久远。 在古代, 人们大都认为圆的周长是直径的 3 倍, 我国古代的数学著作《周髀算经》中就有“周三径一”的记载。古希腊数学家阿基米德发现, 当正多边形的边数增加时, 它的形状就越来越接近圆。 他依据这个想法求出圆周率介于 和 之间。
学以致用
我国魏晋时期数学家刘徽采用“割圆术” 来求圆的周长的近似值。 他从圆的内接正六边形算起, 逐渐把边数加倍, 正十二边形,正二十四边形……求得圆周率的近似值是 3.14。
学以致用
大约 1500 年前, 我国南北朝科学家祖冲之使用刘徽的方法算出圆周率 π 大约在 3.1415926 和 3.1415927 之间, 成为世界上第一个把圆周率的值精确到小数点后 7 位的人。 他还发现一个与 π 值非常接近的分数 (约等于 3.1415929), 这一研究成果比国外数学家早了 1000 多年。
随着数学的发展, 特别是计算机的问世, 圆周率的精确度被算得越来越高。现在,人们已经能够把圆周率精确到小数点后数万亿位。
课后作业
02
完成教材课后习题及练习册同步练习。
课后作业
感 谢 观 看
