第四章 三角形 达标检测卷(含解析)2022—2023学年北师大版七年级数学下册
文档属性
| 名称 | 第四章 三角形 达标检测卷(含解析)2022—2023学年北师大版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 249.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-21 13:05:18 | ||
图片预览

文档简介
第四章 三角形 达标检测卷 北师大版七年级数学下册
一、单选题
1.现有两根木棒,它们的长分别是20cm和30cm.若要钉一个三角架,则下列四根木棒的长度应选( )
A.10cm B.30cm C.50cm D.70cm
2.某同学把三角形的玻璃打碎成了3块,现要到玻璃店配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去
C.带③去 D.①②③都带去
3.如图,下列各组条件中,不能得到的是( )
A., B.,
C., D.,
4.如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离.我们可以证明出△ABC≌△DEC,进而得出AB=DE,那么判定△ABC和△DEC全等的依据是( )
A.SSS B.SAS C.ASA D.AAS
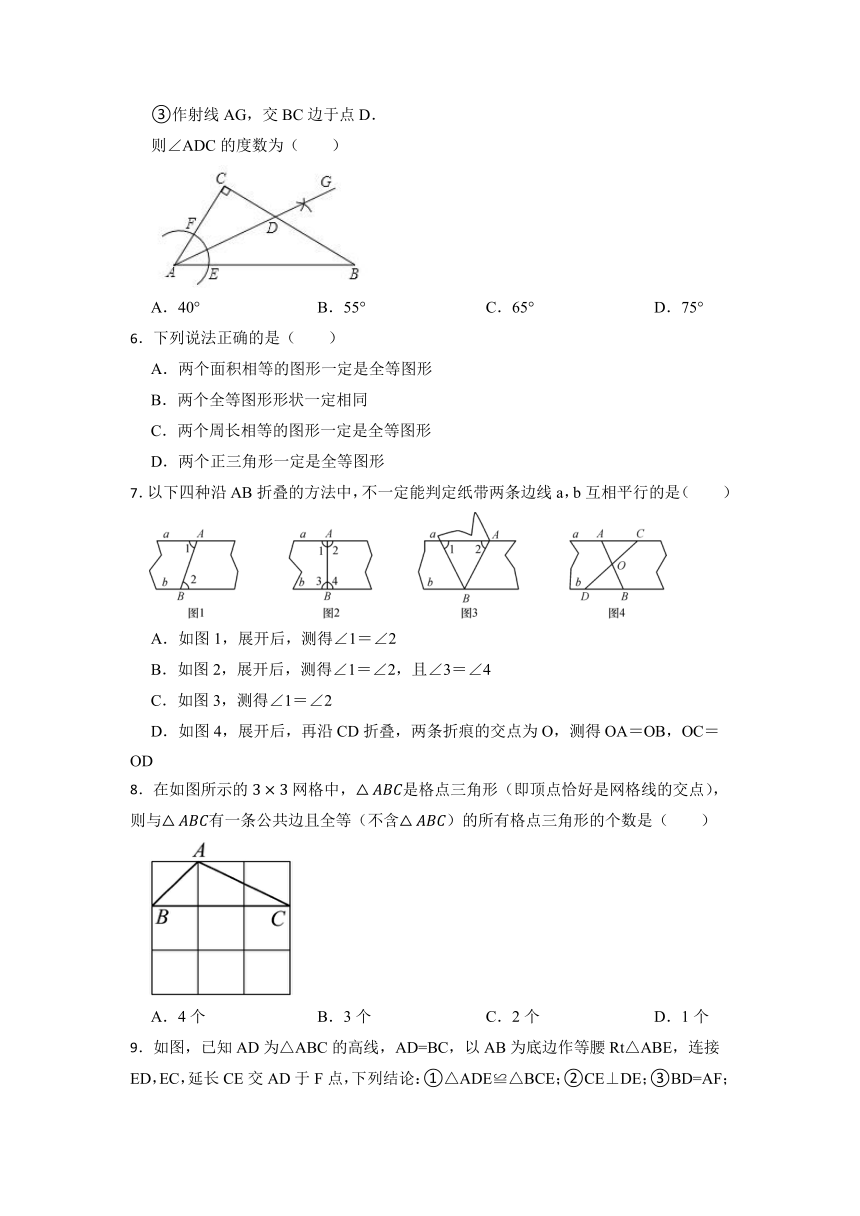
5.如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:
①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于EF长为半径画弧,两弧相交于点G;
③作射线AG,交BC边于点D.
则∠ADC的度数为( )
A.40° B.55° C.65° D.75°
6.下列说法正确的是( )
A.两个面积相等的图形一定是全等图形
B.两个全等图形形状一定相同
C.两个周长相等的图形一定是全等图形
D.两个正三角形一定是全等图形
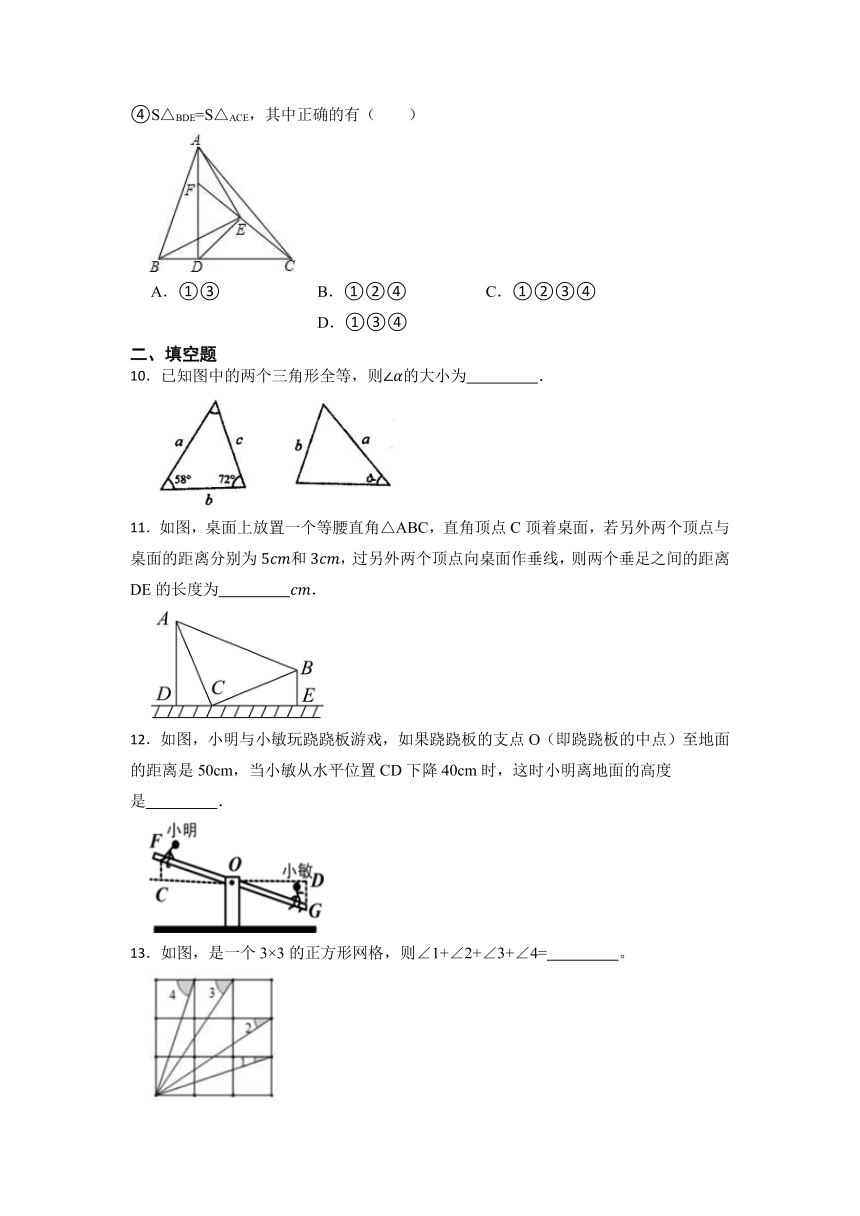
7.以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
A.如图1,展开后,测得∠1=∠2
B.如图2,展开后,测得∠1=∠2,且∠3=∠4
C.如图3,测得∠1=∠2
D.如图4,展开后,再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
8.在如图所示的网格中,是格点三角形(即顶点恰好是网格线的交点),则与有一条公共边且全等(不含)的所有格点三角形的个数是( )
A.4个 B.3个 C.2个 D.1个
9.如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )
A.①③ B.①②④ C.①②③④ D.①③④
二、填空题
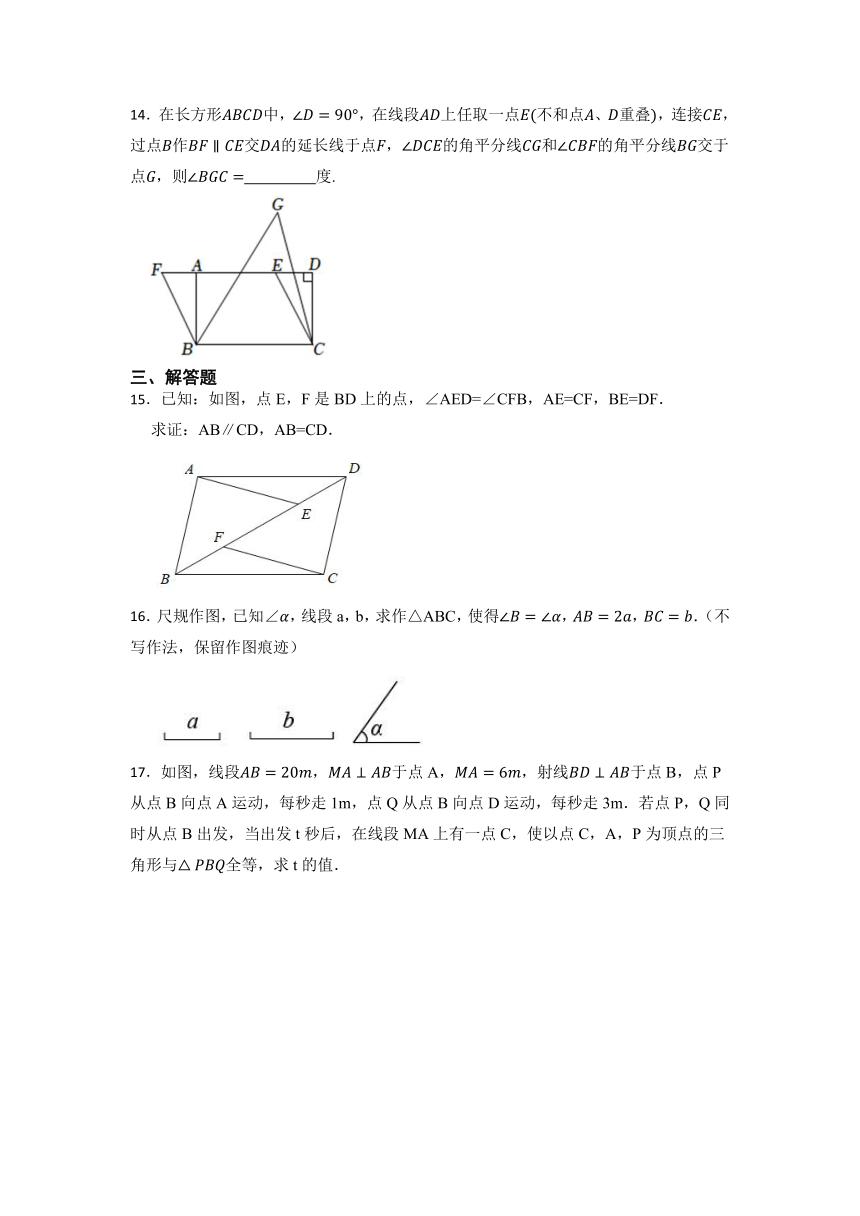
10.已知图中的两个三角形全等,则的大小为 .
11.如图,桌面上放置一个等腰直角△ABC,直角顶点C顶着桌面,若另外两个顶点与桌面的距离分别为和,过另外两个顶点向桌面作垂线,则两个垂足之间的距离DE的长度为 .
12.如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小敏从水平位置CD下降40cm时,这时小明离地面的高度是 .
13.如图,是一个3×3的正方形网格,则∠1+∠2+∠3+∠4= 。
14.在长方形中,,在线段上任取一点不和点、重叠,连接,过点作交的延长线于点,的角平分线和的角平分线交于点,则 度.
三、解答题
15.已知:如图,点E,F是BD上的点,∠AED=∠CFB,AE=CF,BE=DF.
求证:AB∥CD,AB=CD.
16.尺规作图,已知∠,线段a,b,求作△ABC,使得,,.(不写作法,保留作图痕迹)
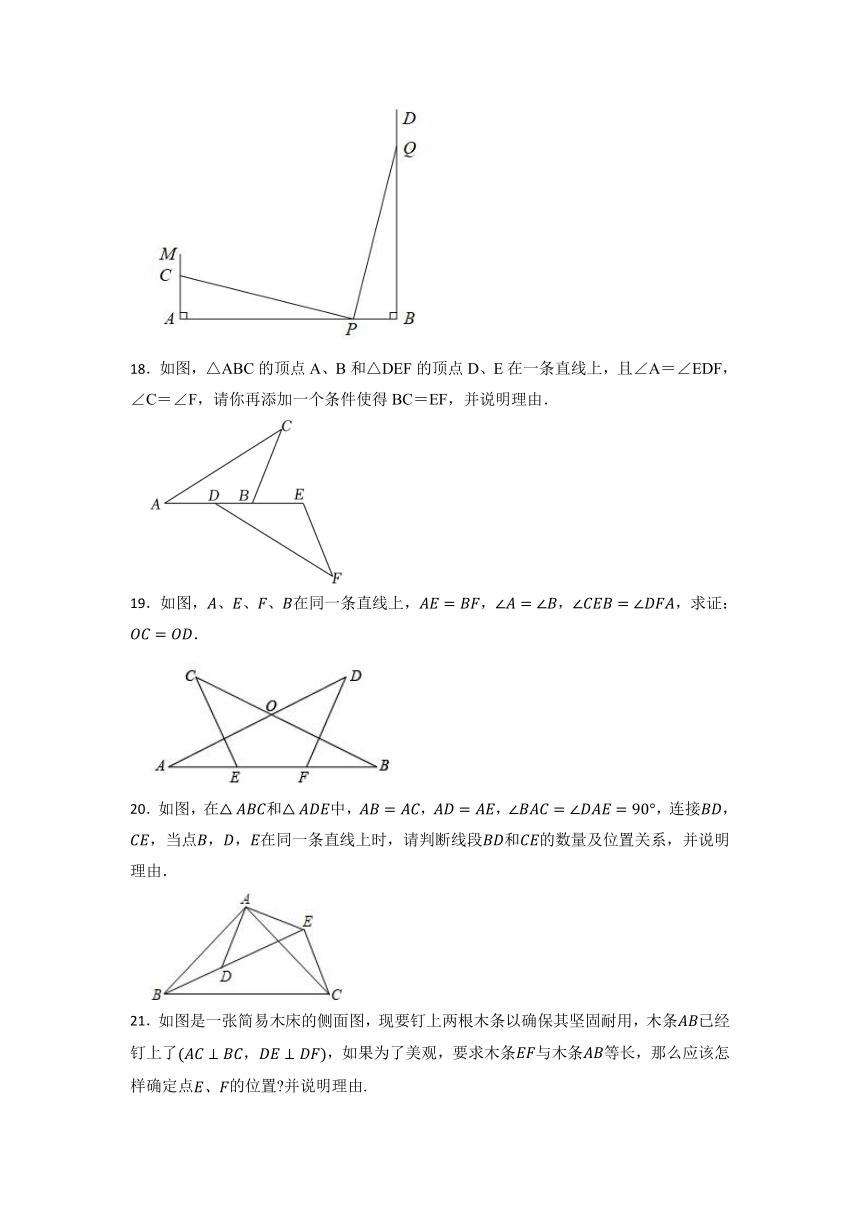
17.如图,线段,于点A,,射线于点B,点P从点B向点A运动,每秒走1m,点Q从点B向点D运动,每秒走3m.若点P,Q同时从点B出发,当出发t秒后,在线段MA上有一点C,使以点C,A,P为顶点的三角形与全等,求t的值.
18.如图,△ABC的顶点A、B和△DEF的顶点D、E在一条直线上,且∠A=∠EDF,∠C=∠F,请你再添加一个条件使得BC=EF,并说明理由.
19.如图,、、、在同一条直线上,,,,求证:.
20.如图,在和中,,,,连接,,当点,,在同一条直线上时,请判断线段和的数量及位置关系,并说明理由.
21.如图是一张简易木床的侧面图,现要钉上两根木条以确保其坚固耐用,木条已经钉上了,如果为了美观,要求木条与木条等长,那么应该怎样确定点的位置 并说明理由.
答案解析部分
1.【答案】B
【解析】【解答】解:根据三角形的三边关系,得
第三根木棒的长度应大于30-20=10(cm),而小于30+20=50(cm).
故答案为:B.
【分析】根据三角形三边关系定理可得“两边之差<第三边<两边之和”可得第三边的范围:10<第三边<50,然后根据各选项即可判断求解.
2.【答案】C
【解析】【解答】解:第①块只保留了原三角形的一个角和部分边,根据这块不能配一块与原来完全一样的;
第②块只保留了原三角形的部分边,根据这两块中的任意一块均不能配一块与原来完全一样的;
第③块不仅保留了原三角形的两个角还保留了一边,则可根据来配一块与原来一样的玻璃.
故答案为:C.
【分析】由于③保留两角一边,根据ASA可得全等三角形.
3.【答案】D
【解析】【解答】解:A、由,,AB=AB,满足SAS能证明,故A不符合题意;
B、,,AB=AB,满足SSS能证明,故B不符合题意;
C、,,AB=AB,满足SAS能证明,故C不符合题意;
D、,,AB=AB,满足SSA,不能证明,故D符合题意;
故答案为:D.
【分析】利用全等三角形的判定方法逐项判断即可。
4.【答案】B
【解析】【解答】解:如图,连接AB,
在△ACB和△DCE中,
,
∴△ACB≌△DCE(SAS),
∴AB=DE
故答案为:B.
【分析】连接AB,利用“SAS”证明△ACB≌△DCE,利用全等三角形的对应边相等,可证得结论.
5.【答案】C
【解析】【解答】解:根据作图方法可得AG是∠CAB的角平分线,
∵∠CAB=50°,
∴∠CAD=∠CAB=25°,
∵∠C=90°,
∴∠CDA=90°﹣25°=65°,
故选:C.
【分析】根据角平分线的作法可得AG是∠CAB的角平分线,然后再根据角平分线的性质可得∠CAD=∠CAB=25°,然后再根据直角三角形的性质可得∠CDA=90°﹣25°=65°.
6.【答案】B
【解析】【解答】解:A、能够完全重合的两个图形就是全等形,所以两个面积相等的图形不一定是全等图形,故A错误,不符合题意;
B、两个全等图形形状一定相同,故B正确,符合题意;
C、两个周长相等的图形不一定是全等图形,故C错误,不符合题意;
D、两个正三角形只是形状相同,大小不一定相等,所以不一定是全等图形,故D错误,不符合题意.
故答案为:B.
【分析】能够完全重合的两个图形就是全等形,全等图形的大小、形状都一样,故全等图形的面积、周长都相等,但周长相等、面积相等的图形不一定是全等图形,据此一一判断得出答案.
7.【答案】C
【解析】【解答】解:A、∵∠1=∠2,
∴a∥b,故A不符合题意;
B、∵∠1=∠2,且∠3=∠4 ,∠1+∠2=180°,∠3+∠4=180°,
∴∠1=∠2=∠3=∠4=90°,
∴a∥b,故B不符合题意;
C、∠1=∠2不能证明a∥b,故C符合题意;
D、在△AOC和△BOD中
∴△AOC≌△BOD(SAS),
∴∠CAO=∠DBO,
∴a∥b,故D不符合题意;
故答案为:C
【分析】利用内错角相等,两直线平行,可对A作出判断;利用邻补角的定义,可得到∠1=∠2=∠3=∠4,利用内错角相等,两直线平行,可对B作出判断;利用平行线的判定定理,可对C作出判断;利用SAS证明△AOC≌△BOD,利用全等三角形的对应角相等,可知∠CAO=∠DBO,然后利用内错角相等,两直线平行,可证得a∥b,可对D作出判断.
8.【答案】A
【解析】【解答】解:如图所示,
以BC为公共边的全等三角形有三个分别为,,,
以AB为公共边的全等三角形有一个为,
∴共有4个三角形与△ABC有一条公共边且全等,
故答案为:A.
【分析】根据全等三角形的判定,结合图形求解即可。
9.【答案】C
【解析】【解答】①∵AD为△ABC的高线,∴∠CBE+∠ABE+∠BAD=90°.
∵Rt△ABE是等腰直角三角形,∴∠ABE=∠BAE=∠BAD+∠DAE=45°,AE=BE,∴∠CBE+∠BAD=45°,∴∠DAE=∠CBE.在△DAE和△CBE中,∵,∴△ADE≌△BCE(SAS);故①符合题意;
②∵△ADE≌△BCE,∴∠EDA=∠ECB.
∵∠ADE+∠EDC=90°,∴∠EDC+∠ECB=90°,∴∠DEC=90°,∴CE⊥DE;故②符合题意;
③∵∠BDE=∠ADB+∠ADE,∠AFE=∠ADC+∠ECD,∴∠BDE=∠AFE.
∵∠BED+∠BEF=∠AEF+∠BEF=90°,∴∠BED=∠AEF.
在△AEF和△BED中,∵,∴△AEF≌△BED(AAS),∴BD=AF;故③符合题意;
④∵AD=BC,BD=AF,∴CD=DF.
∵AD⊥BC,∴△FDC是等腰直角三角形.
∵DE⊥CE,∴EF=CE,∴S△AEF=S△ACE.
∵△AEF≌△BED,∴S△AEF=S△BED,∴S△BDE=S△ACE.故④符合题意.
故答案为:C.
【分析】全等三角形的判定与性质的综合应用。
10.【答案】50°
【解析】【解答】解:根据全等三角形的性质可知,两个三角形中边长为b的边所对的角相等,
因此,
故答案为:50°.
【分析】利用全等三角形的性质可得。
11.【答案】8
【解析】【解答】解:∵∠CDA=∠ACB=∠CEB=90°,
∴∠ACD +∠DAC=∠ACD+∠ECB=∠ECB+∠CBE=90°,
∴∠ACD =∠CBE,∠DAC=∠ECB,
在△ACD和△CBE中
,
∴△ACD≌△CBE(ASA),
∴AD=CE,CD=BE,
∴DE=DC+CE=BE+AD=3+5=8(cm).
故答案为:8.
【分析】先利用“ASA”证明△ACD≌△CBE可得AD=CE,CD=BE,再利用线段的和差及等量代换可得DE=DC+CE=BE+AD=3+5=8。
12.【答案】90cm
【解析】【解答】∵O是CD和FG的中点,
∴FO=OG,CO=DO,
又∠FOC=∠GOD,
∴ΔFOC≌ΔGOD,
∴FC=GD=40cm,
∴小明离地面的高度是:50+40=90cm.
【分析】小明此时的高度等于,注意离地高度。
13.【答案】180°
【解析】【解答】解:对图中的点进行标注,如图所示,设正方形网格的单位长度为1.
∵ 如图是一个3×3的正方形网格
∴
∵正方形网格的单位长度为1
∴BC=AE=1,AB=ED=MN=3,BF=AN=2
∵BC=AE=1,,AB=ED
∴ABC≌DEA(SAS)
∴
∵在AED中,
∴
∴
同理可得:
∴∠1+∠2+∠3+∠4= 180°
故答案为:180°.
【分析】根据全等三角形的判定可以得到ABC≌DEA,从而得知,结合直角三角形的性质得到 ,继而得到了,同理可以得到,即可以求出∠1+∠2+∠3+∠4= 180°
14.【答案】45
【解析】【解答】解:四边形ABCD是长方形,
∴,
,
∵,
,
,
是的角平分线,是的角平分线,
,,
设,则,
,
,
,
,
故答案为:45.
【分析】由矩形的性质得AD∥BC,由平行线的性质得∠AEC+∠BCE=180°,∠CBF+∠BCE=180°,根据同角的补角相等得∠CBF=∠AEC,根据角平分线的定义得∠ECG=∠DCG,∠CBG=∠FBG,设∠ECG=∠DCG=x,用含x的式子表示出∠BCE、∠CBF及∠CBG,最后根据三角形的内角和定理计算即可.
15.【答案】证明:∵∠AED=∠CFB,
∴∠AEB=∠CFD,
∵AE=CF,BE=DF,
∴△ABE≌△CDF(SAS),
∴AB=CD,∠ABD=∠CDB,
∴AB∥CD.
【解析】【分析】先利用“SAS”证明△ABE≌△CDF可得AB=CD,∠ABD=∠CDB,即可得到AB∥CD。
16.【答案】解:即为所求作的三角形,
【解析】【分析】作∠B=∠α,然后截取AB=2a,BC=b,再连接AC即可.
17.【答案】解:当△APC≌△BQP时,AP=BQ,即20-t=3t,
解得:t=5;
当△APC≌△BPQ时,AP=BP=AB=10m,
此时所用时间为10秒,AC=BQ=10m,不合题意,舍去;
综上,出发5秒后,在线段MA上有一点C,使以点C,A,P为顶点的三角形与△PBQ全等.
【解析】【分析】分两种情况:①当△APC≌△BQP时,②当△APC≌△BPQ时,再分别列出方程求解即可。
18.【答案】解:添加的条件为AC=DF,理由如下:
在△ABC和△DEF,
,
∴△ABC≌△DEF(ASA),
∴BC=EF.
【解析】【分析】三角形全等的判定定理有:边角边、角角边、角边角和边边边定理,根据三角形全等的条件添加条件,再根据全等三角形的性质,即可得出结论.
19.【答案】解:∵AE=BF,
∴AE+EF=BF+EF,即AF=BE,
在△AFD和△BEC中,
,
∴△AFD≌△BEC(ASA),
∴AD=BC,
∵∠A=∠B,
∴OA=OB,
∴AD-OA=BC-OB,
即OD=OC.
【解析】【分析】先证出△AFD≌△BEC(ASA),可得AD=BC,再结合OA=OB,利用线段的和差求出即可。
20.【答案】解:结论:且;
理由如下:
,
.
.
在和中
,
≌(SAS)
,,
,
,
即,
,
.
【解析】【分析】利用“SAS”证明 ≌,可得 ,,再求出,然后利用三角形的内角和可得,从而可得。
21.【答案】解:利用刻度尺测量使BC=DF,AC=DE,此时木条EF与木条AB等长.
理由:∵AC⊥BC,DE⊥DF,
∴∠ACB=∠EDF=90°,
在△ACB和△EDF中
∴△ACB≌△EDF(SAS)
∴EF=AB.
∴使BC=DF,AC=DE,此时木条EF与木条AB等长.
【解析】【分析】利用垂直的定义可证得∠ACB=∠EDF=90°,利用SAS证明△ACB≌△EDF,利用全等三角形的对应边相等,可证得EF=AB,即可求解.
一、单选题
1.现有两根木棒,它们的长分别是20cm和30cm.若要钉一个三角架,则下列四根木棒的长度应选( )
A.10cm B.30cm C.50cm D.70cm
2.某同学把三角形的玻璃打碎成了3块,现要到玻璃店配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去
C.带③去 D.①②③都带去
3.如图,下列各组条件中,不能得到的是( )
A., B.,
C., D.,
4.如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离.我们可以证明出△ABC≌△DEC,进而得出AB=DE,那么判定△ABC和△DEC全等的依据是( )
A.SSS B.SAS C.ASA D.AAS
5.如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:
①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于EF长为半径画弧,两弧相交于点G;
③作射线AG,交BC边于点D.
则∠ADC的度数为( )
A.40° B.55° C.65° D.75°
6.下列说法正确的是( )
A.两个面积相等的图形一定是全等图形
B.两个全等图形形状一定相同
C.两个周长相等的图形一定是全等图形
D.两个正三角形一定是全等图形
7.以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
A.如图1,展开后,测得∠1=∠2
B.如图2,展开后,测得∠1=∠2,且∠3=∠4
C.如图3,测得∠1=∠2
D.如图4,展开后,再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
8.在如图所示的网格中,是格点三角形(即顶点恰好是网格线的交点),则与有一条公共边且全等(不含)的所有格点三角形的个数是( )
A.4个 B.3个 C.2个 D.1个
9.如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )
A.①③ B.①②④ C.①②③④ D.①③④
二、填空题
10.已知图中的两个三角形全等,则的大小为 .
11.如图,桌面上放置一个等腰直角△ABC,直角顶点C顶着桌面,若另外两个顶点与桌面的距离分别为和,过另外两个顶点向桌面作垂线,则两个垂足之间的距离DE的长度为 .
12.如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小敏从水平位置CD下降40cm时,这时小明离地面的高度是 .
13.如图,是一个3×3的正方形网格,则∠1+∠2+∠3+∠4= 。
14.在长方形中,,在线段上任取一点不和点、重叠,连接,过点作交的延长线于点,的角平分线和的角平分线交于点,则 度.
三、解答题
15.已知:如图,点E,F是BD上的点,∠AED=∠CFB,AE=CF,BE=DF.
求证:AB∥CD,AB=CD.
16.尺规作图,已知∠,线段a,b,求作△ABC,使得,,.(不写作法,保留作图痕迹)
17.如图,线段,于点A,,射线于点B,点P从点B向点A运动,每秒走1m,点Q从点B向点D运动,每秒走3m.若点P,Q同时从点B出发,当出发t秒后,在线段MA上有一点C,使以点C,A,P为顶点的三角形与全等,求t的值.
18.如图,△ABC的顶点A、B和△DEF的顶点D、E在一条直线上,且∠A=∠EDF,∠C=∠F,请你再添加一个条件使得BC=EF,并说明理由.
19.如图,、、、在同一条直线上,,,,求证:.
20.如图,在和中,,,,连接,,当点,,在同一条直线上时,请判断线段和的数量及位置关系,并说明理由.
21.如图是一张简易木床的侧面图,现要钉上两根木条以确保其坚固耐用,木条已经钉上了,如果为了美观,要求木条与木条等长,那么应该怎样确定点的位置 并说明理由.
答案解析部分
1.【答案】B
【解析】【解答】解:根据三角形的三边关系,得
第三根木棒的长度应大于30-20=10(cm),而小于30+20=50(cm).
故答案为:B.
【分析】根据三角形三边关系定理可得“两边之差<第三边<两边之和”可得第三边的范围:10<第三边<50,然后根据各选项即可判断求解.
2.【答案】C
【解析】【解答】解:第①块只保留了原三角形的一个角和部分边,根据这块不能配一块与原来完全一样的;
第②块只保留了原三角形的部分边,根据这两块中的任意一块均不能配一块与原来完全一样的;
第③块不仅保留了原三角形的两个角还保留了一边,则可根据来配一块与原来一样的玻璃.
故答案为:C.
【分析】由于③保留两角一边,根据ASA可得全等三角形.
3.【答案】D
【解析】【解答】解:A、由,,AB=AB,满足SAS能证明,故A不符合题意;
B、,,AB=AB,满足SSS能证明,故B不符合题意;
C、,,AB=AB,满足SAS能证明,故C不符合题意;
D、,,AB=AB,满足SSA,不能证明,故D符合题意;
故答案为:D.
【分析】利用全等三角形的判定方法逐项判断即可。
4.【答案】B
【解析】【解答】解:如图,连接AB,
在△ACB和△DCE中,
,
∴△ACB≌△DCE(SAS),
∴AB=DE
故答案为:B.
【分析】连接AB,利用“SAS”证明△ACB≌△DCE,利用全等三角形的对应边相等,可证得结论.
5.【答案】C
【解析】【解答】解:根据作图方法可得AG是∠CAB的角平分线,
∵∠CAB=50°,
∴∠CAD=∠CAB=25°,
∵∠C=90°,
∴∠CDA=90°﹣25°=65°,
故选:C.
【分析】根据角平分线的作法可得AG是∠CAB的角平分线,然后再根据角平分线的性质可得∠CAD=∠CAB=25°,然后再根据直角三角形的性质可得∠CDA=90°﹣25°=65°.
6.【答案】B
【解析】【解答】解:A、能够完全重合的两个图形就是全等形,所以两个面积相等的图形不一定是全等图形,故A错误,不符合题意;
B、两个全等图形形状一定相同,故B正确,符合题意;
C、两个周长相等的图形不一定是全等图形,故C错误,不符合题意;
D、两个正三角形只是形状相同,大小不一定相等,所以不一定是全等图形,故D错误,不符合题意.
故答案为:B.
【分析】能够完全重合的两个图形就是全等形,全等图形的大小、形状都一样,故全等图形的面积、周长都相等,但周长相等、面积相等的图形不一定是全等图形,据此一一判断得出答案.
7.【答案】C
【解析】【解答】解:A、∵∠1=∠2,
∴a∥b,故A不符合题意;
B、∵∠1=∠2,且∠3=∠4 ,∠1+∠2=180°,∠3+∠4=180°,
∴∠1=∠2=∠3=∠4=90°,
∴a∥b,故B不符合题意;
C、∠1=∠2不能证明a∥b,故C符合题意;
D、在△AOC和△BOD中
∴△AOC≌△BOD(SAS),
∴∠CAO=∠DBO,
∴a∥b,故D不符合题意;
故答案为:C
【分析】利用内错角相等,两直线平行,可对A作出判断;利用邻补角的定义,可得到∠1=∠2=∠3=∠4,利用内错角相等,两直线平行,可对B作出判断;利用平行线的判定定理,可对C作出判断;利用SAS证明△AOC≌△BOD,利用全等三角形的对应角相等,可知∠CAO=∠DBO,然后利用内错角相等,两直线平行,可证得a∥b,可对D作出判断.
8.【答案】A
【解析】【解答】解:如图所示,
以BC为公共边的全等三角形有三个分别为,,,
以AB为公共边的全等三角形有一个为,
∴共有4个三角形与△ABC有一条公共边且全等,
故答案为:A.
【分析】根据全等三角形的判定,结合图形求解即可。
9.【答案】C
【解析】【解答】①∵AD为△ABC的高线,∴∠CBE+∠ABE+∠BAD=90°.
∵Rt△ABE是等腰直角三角形,∴∠ABE=∠BAE=∠BAD+∠DAE=45°,AE=BE,∴∠CBE+∠BAD=45°,∴∠DAE=∠CBE.在△DAE和△CBE中,∵,∴△ADE≌△BCE(SAS);故①符合题意;
②∵△ADE≌△BCE,∴∠EDA=∠ECB.
∵∠ADE+∠EDC=90°,∴∠EDC+∠ECB=90°,∴∠DEC=90°,∴CE⊥DE;故②符合题意;
③∵∠BDE=∠ADB+∠ADE,∠AFE=∠ADC+∠ECD,∴∠BDE=∠AFE.
∵∠BED+∠BEF=∠AEF+∠BEF=90°,∴∠BED=∠AEF.
在△AEF和△BED中,∵,∴△AEF≌△BED(AAS),∴BD=AF;故③符合题意;
④∵AD=BC,BD=AF,∴CD=DF.
∵AD⊥BC,∴△FDC是等腰直角三角形.
∵DE⊥CE,∴EF=CE,∴S△AEF=S△ACE.
∵△AEF≌△BED,∴S△AEF=S△BED,∴S△BDE=S△ACE.故④符合题意.
故答案为:C.
【分析】全等三角形的判定与性质的综合应用。
10.【答案】50°
【解析】【解答】解:根据全等三角形的性质可知,两个三角形中边长为b的边所对的角相等,
因此,
故答案为:50°.
【分析】利用全等三角形的性质可得。
11.【答案】8
【解析】【解答】解:∵∠CDA=∠ACB=∠CEB=90°,
∴∠ACD +∠DAC=∠ACD+∠ECB=∠ECB+∠CBE=90°,
∴∠ACD =∠CBE,∠DAC=∠ECB,
在△ACD和△CBE中
,
∴△ACD≌△CBE(ASA),
∴AD=CE,CD=BE,
∴DE=DC+CE=BE+AD=3+5=8(cm).
故答案为:8.
【分析】先利用“ASA”证明△ACD≌△CBE可得AD=CE,CD=BE,再利用线段的和差及等量代换可得DE=DC+CE=BE+AD=3+5=8。
12.【答案】90cm
【解析】【解答】∵O是CD和FG的中点,
∴FO=OG,CO=DO,
又∠FOC=∠GOD,
∴ΔFOC≌ΔGOD,
∴FC=GD=40cm,
∴小明离地面的高度是:50+40=90cm.
【分析】小明此时的高度等于,注意离地高度。
13.【答案】180°
【解析】【解答】解:对图中的点进行标注,如图所示,设正方形网格的单位长度为1.
∵ 如图是一个3×3的正方形网格
∴
∵正方形网格的单位长度为1
∴BC=AE=1,AB=ED=MN=3,BF=AN=2
∵BC=AE=1,,AB=ED
∴ABC≌DEA(SAS)
∴
∵在AED中,
∴
∴
同理可得:
∴∠1+∠2+∠3+∠4= 180°
故答案为:180°.
【分析】根据全等三角形的判定可以得到ABC≌DEA,从而得知,结合直角三角形的性质得到 ,继而得到了,同理可以得到,即可以求出∠1+∠2+∠3+∠4= 180°
14.【答案】45
【解析】【解答】解:四边形ABCD是长方形,
∴,
,
∵,
,
,
是的角平分线,是的角平分线,
,,
设,则,
,
,
,
,
故答案为:45.
【分析】由矩形的性质得AD∥BC,由平行线的性质得∠AEC+∠BCE=180°,∠CBF+∠BCE=180°,根据同角的补角相等得∠CBF=∠AEC,根据角平分线的定义得∠ECG=∠DCG,∠CBG=∠FBG,设∠ECG=∠DCG=x,用含x的式子表示出∠BCE、∠CBF及∠CBG,最后根据三角形的内角和定理计算即可.
15.【答案】证明:∵∠AED=∠CFB,
∴∠AEB=∠CFD,
∵AE=CF,BE=DF,
∴△ABE≌△CDF(SAS),
∴AB=CD,∠ABD=∠CDB,
∴AB∥CD.
【解析】【分析】先利用“SAS”证明△ABE≌△CDF可得AB=CD,∠ABD=∠CDB,即可得到AB∥CD。
16.【答案】解:即为所求作的三角形,
【解析】【分析】作∠B=∠α,然后截取AB=2a,BC=b,再连接AC即可.
17.【答案】解:当△APC≌△BQP时,AP=BQ,即20-t=3t,
解得:t=5;
当△APC≌△BPQ时,AP=BP=AB=10m,
此时所用时间为10秒,AC=BQ=10m,不合题意,舍去;
综上,出发5秒后,在线段MA上有一点C,使以点C,A,P为顶点的三角形与△PBQ全等.
【解析】【分析】分两种情况:①当△APC≌△BQP时,②当△APC≌△BPQ时,再分别列出方程求解即可。
18.【答案】解:添加的条件为AC=DF,理由如下:
在△ABC和△DEF,
,
∴△ABC≌△DEF(ASA),
∴BC=EF.
【解析】【分析】三角形全等的判定定理有:边角边、角角边、角边角和边边边定理,根据三角形全等的条件添加条件,再根据全等三角形的性质,即可得出结论.
19.【答案】解:∵AE=BF,
∴AE+EF=BF+EF,即AF=BE,
在△AFD和△BEC中,
,
∴△AFD≌△BEC(ASA),
∴AD=BC,
∵∠A=∠B,
∴OA=OB,
∴AD-OA=BC-OB,
即OD=OC.
【解析】【分析】先证出△AFD≌△BEC(ASA),可得AD=BC,再结合OA=OB,利用线段的和差求出即可。
20.【答案】解:结论:且;
理由如下:
,
.
.
在和中
,
≌(SAS)
,,
,
,
即,
,
.
【解析】【分析】利用“SAS”证明 ≌,可得 ,,再求出,然后利用三角形的内角和可得,从而可得。
21.【答案】解:利用刻度尺测量使BC=DF,AC=DE,此时木条EF与木条AB等长.
理由:∵AC⊥BC,DE⊥DF,
∴∠ACB=∠EDF=90°,
在△ACB和△EDF中
∴△ACB≌△EDF(SAS)
∴EF=AB.
∴使BC=DF,AC=DE,此时木条EF与木条AB等长.
【解析】【分析】利用垂直的定义可证得∠ACB=∠EDF=90°,利用SAS证明△ACB≌△EDF,利用全等三角形的对应边相等,可证得EF=AB,即可求解.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
