人教A版(2019)必修二 10.1.2 事件的关系和运算 教学设计(表格式)
文档属性
| 名称 | 人教A版(2019)必修二 10.1.2 事件的关系和运算 教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 482.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-19 21:12:45 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 高中数学 年级 高一 学期 春季
课题 10.1.2事件的关系和运算
教科书 书 名:普通高中教科书数学必修第二册 出版社:人民教育出版社 出版日期:2019年6月
教学目标
1. 理解事件的关系与运算. 2. 通过事件之间的运算,理解互斥事件和对立事件的概念.
教学内容
教学重点:事件运算关系的实际含义. 教学难点:事件运算关系的应用.
教学过程
一、情景导入 在掷骰子的试验中,可以定义许多事件.例如,事件C1={出现1点},事件C2={出现2点},事件C3={出现3点},事件C4={出现4点},事件C5={出现5点},事件C6={出现6点},事件D1={出现的点数不大于1},事件D2={出现的点数大于3},事件D3={出现的点数小于5},事件E={出现的点数小于7},事件F={出现的点数为偶数},事件G={出现的点数为奇数}…… 你还能写出这个实验中其他一些事件吗?请用集合的形式表示这些事件.借助集合与集合的关系和运算,你能发现这些事件之间的联系吗? 要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探. 二、预习课本,引入新课 阅读课本229-232页,思考并完成以下问题 1.事件的关系或运算的含义? 要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。 三、新知探究 课本研读】阅读课本,学习记忆相关概念. 包含关系定义一般地,若事件发生,则事件一定发生, 我们就称事件包含事件. (或事件包含于事件)含义发生导致发生符号表示 (或)图形表示特殊情形如果事件包含事件,事件也包含事件,即且,则称事件与事件相等,记作
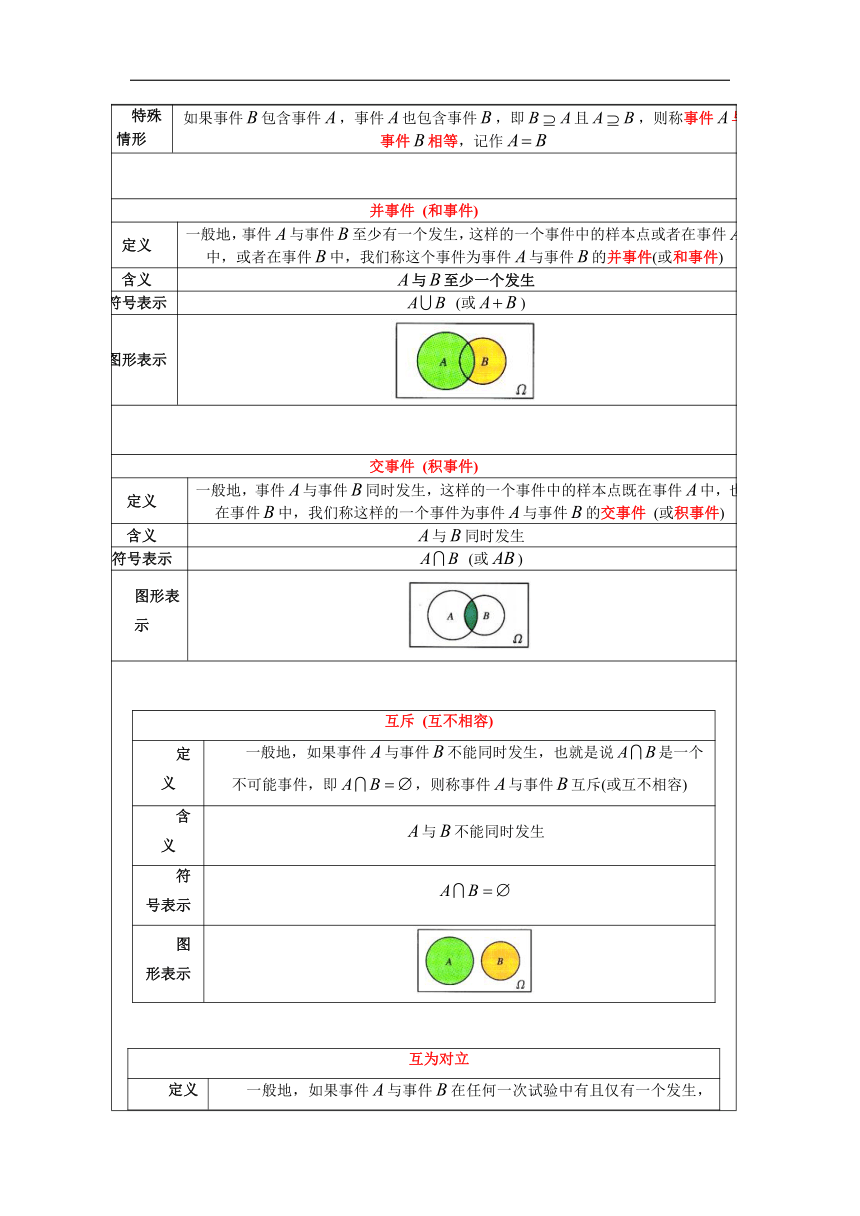
并事件 (和事件)定义一般地,事件与事件至少有一个发生,这样的一个事件中的样本点或者在事件中,或者在事件中,我们称这个事件为事件与事件的并事件(或和事件)含义与至少一个发生符号表示 (或)图形表示
交事件 (积事件)定义一般地,事件与事件同时发生,这样的一个事件中的样本点既在事件中,也在事件中,我们称这样的一个事件为事件与事件的交事件 (或积事件)含义与同时发生符号表示 (或)图形表示
互斥 (互不相容)定义一般地,如果事件与事件不能同时发生,也就是说是一个不可能事件,即,则称事件与事件互斥(或互不相容)含义与不能同时发生符号表示图形表示
互为对立定义一般地,如果事件与事件在任何一次试验中有且仅有一个发生,即,且,那么称事件与事件互为对立.事件的对立事件记为.含义与有且仅有一个发生符号表示,图形表示
事件的关系或运算的含义,以及相应的符号表示事件的关系或运算含义符号表示包含发生导致发生并事件(和事件)与至少一个发生 或交事件(积事件)与同时发生或互斥(互不相容)与不能同时发生互为对立与有且仅有一个发生,
【推广】可以定义多个事件的和事件以及积事件. 例如,对于三个事件, (或)发生当且仅当中至少一个发生, (或 )发生当且仅当同时发生,等等. 四、典例分析、举一反三 例5 如图, 由甲、乙两个元件组成一个并联电路,每个元件可能正常或失效. 设事件 “甲元件正常”,“乙元件正常”. (1)写出表示两个元件工作状态的样本空间; (2)用集合的形式表示事件以及它们的对立事件; (3)用集合的形式表示事件和事件,并说明它们的含义及关系. 解:(1)用分别表示甲,乙两个元件的状态,则可以用 表示这个并联电路的状态,以1表示元件正常,0表示元件失效,则样本空间为. (2)根据题意,可得, , (3), 表示电路工作正常,表示电路工作不正常;和互为对立事件. 例6 一个袋子中有大小和质地相同的4个球,其中有2个红色球(标号为1和2),2个绿色球(标号为3和4),从袋中不放回地依次随机摸出2个球. 设事件“第一次摸到红球”,“第二次摸到红球”,“两次都摸到红球”, “两次都摸到绿球”, “两个球颜色相同”,“两个球颜色不同”. (1)用集合的形式分别写出试验的样本空间以及上述各事件; (2)事件与,与, 与之间各有什么关系 (3)事件与事件的并事件与事件有什么关系 事件与事件的交事件与事件有什么关系 解:(1)所有的试验结果如图所示,用数组表示可能的结果, 是第一次摸到的球的标号,是第二次摸到的球的标号, 则试验的样本空间 事件“第一次摸到红球”,即1或2,于是 事件“第二次摸到红球”,即1或2,于是 同理,有,,, (2)因为,所以事件包含事件; 因为,所以事件与事件互斥; 因为,,所以事件与事件互为对立事件. (3)因为,所以事件是事件与事件的并事件; 因为,所以事件是事件与事件的交事件. 【小组互动】完成课本练习1、2,同桌交换检查,老师答疑. 反思感悟 事件间运算方法 (1)利用事件间运算的定义.列出同一条件下的试验所有可能出现的结果,分析并利用这些结果进行事件间的运算. (2)利用Venn图.借助集合间运算的思想,分析同一条件下的试验所有可能出现的结果,把这些结果在图中列出,进行运算. 五、课堂小结 (1)事件的包含关系与相等关系. (2)交事件和并事件. (3)互斥事件和对立事件. 2.方法归纳:列举法、Venn图法. 3.常见误区:互斥事件和对立事件之间的关系易混淆.
课程基本信息
学科 高中数学 年级 高一 学期 春季
课题 10.1.2事件的关系和运算
教科书 书 名:普通高中教科书数学必修第二册 出版社:人民教育出版社 出版日期:2019年6月
教学目标
1. 理解事件的关系与运算. 2. 通过事件之间的运算,理解互斥事件和对立事件的概念.
教学内容
教学重点:事件运算关系的实际含义. 教学难点:事件运算关系的应用.
教学过程
一、情景导入 在掷骰子的试验中,可以定义许多事件.例如,事件C1={出现1点},事件C2={出现2点},事件C3={出现3点},事件C4={出现4点},事件C5={出现5点},事件C6={出现6点},事件D1={出现的点数不大于1},事件D2={出现的点数大于3},事件D3={出现的点数小于5},事件E={出现的点数小于7},事件F={出现的点数为偶数},事件G={出现的点数为奇数}…… 你还能写出这个实验中其他一些事件吗?请用集合的形式表示这些事件.借助集合与集合的关系和运算,你能发现这些事件之间的联系吗? 要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探. 二、预习课本,引入新课 阅读课本229-232页,思考并完成以下问题 1.事件的关系或运算的含义? 要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。 三、新知探究 课本研读】阅读课本,学习记忆相关概念. 包含关系定义一般地,若事件发生,则事件一定发生, 我们就称事件包含事件. (或事件包含于事件)含义发生导致发生符号表示 (或)图形表示特殊情形如果事件包含事件,事件也包含事件,即且,则称事件与事件相等,记作
并事件 (和事件)定义一般地,事件与事件至少有一个发生,这样的一个事件中的样本点或者在事件中,或者在事件中,我们称这个事件为事件与事件的并事件(或和事件)含义与至少一个发生符号表示 (或)图形表示
交事件 (积事件)定义一般地,事件与事件同时发生,这样的一个事件中的样本点既在事件中,也在事件中,我们称这样的一个事件为事件与事件的交事件 (或积事件)含义与同时发生符号表示 (或)图形表示
互斥 (互不相容)定义一般地,如果事件与事件不能同时发生,也就是说是一个不可能事件,即,则称事件与事件互斥(或互不相容)含义与不能同时发生符号表示图形表示
互为对立定义一般地,如果事件与事件在任何一次试验中有且仅有一个发生,即,且,那么称事件与事件互为对立.事件的对立事件记为.含义与有且仅有一个发生符号表示,图形表示
事件的关系或运算的含义,以及相应的符号表示事件的关系或运算含义符号表示包含发生导致发生并事件(和事件)与至少一个发生 或交事件(积事件)与同时发生或互斥(互不相容)与不能同时发生互为对立与有且仅有一个发生,
【推广】可以定义多个事件的和事件以及积事件. 例如,对于三个事件, (或)发生当且仅当中至少一个发生, (或 )发生当且仅当同时发生,等等. 四、典例分析、举一反三 例5 如图, 由甲、乙两个元件组成一个并联电路,每个元件可能正常或失效. 设事件 “甲元件正常”,“乙元件正常”. (1)写出表示两个元件工作状态的样本空间; (2)用集合的形式表示事件以及它们的对立事件; (3)用集合的形式表示事件和事件,并说明它们的含义及关系. 解:(1)用分别表示甲,乙两个元件的状态,则可以用 表示这个并联电路的状态,以1表示元件正常,0表示元件失效,则样本空间为. (2)根据题意,可得, , (3), 表示电路工作正常,表示电路工作不正常;和互为对立事件. 例6 一个袋子中有大小和质地相同的4个球,其中有2个红色球(标号为1和2),2个绿色球(标号为3和4),从袋中不放回地依次随机摸出2个球. 设事件“第一次摸到红球”,“第二次摸到红球”,“两次都摸到红球”, “两次都摸到绿球”, “两个球颜色相同”,“两个球颜色不同”. (1)用集合的形式分别写出试验的样本空间以及上述各事件; (2)事件与,与, 与之间各有什么关系 (3)事件与事件的并事件与事件有什么关系 事件与事件的交事件与事件有什么关系 解:(1)所有的试验结果如图所示,用数组表示可能的结果, 是第一次摸到的球的标号,是第二次摸到的球的标号, 则试验的样本空间 事件“第一次摸到红球”,即1或2,于是 事件“第二次摸到红球”,即1或2,于是 同理,有,,, (2)因为,所以事件包含事件; 因为,所以事件与事件互斥; 因为,,所以事件与事件互为对立事件. (3)因为,所以事件是事件与事件的并事件; 因为,所以事件是事件与事件的交事件. 【小组互动】完成课本练习1、2,同桌交换检查,老师答疑. 反思感悟 事件间运算方法 (1)利用事件间运算的定义.列出同一条件下的试验所有可能出现的结果,分析并利用这些结果进行事件间的运算. (2)利用Venn图.借助集合间运算的思想,分析同一条件下的试验所有可能出现的结果,把这些结果在图中列出,进行运算. 五、课堂小结 (1)事件的包含关系与相等关系. (2)交事件和并事件. (3)互斥事件和对立事件. 2.方法归纳:列举法、Venn图法. 3.常见误区:互斥事件和对立事件之间的关系易混淆.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
