人教A版(2019)必修二 10.1.2 事件的关系和运算 (课件31张)
文档属性
| 名称 | 人教A版(2019)必修二 10.1.2 事件的关系和运算 (课件31张) |  | |
| 格式 | pptx | ||
| 文件大小 | 714.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-19 21:14:53 | ||
图片预览






文档简介
(共31张PPT)
10.1.2事件的关系与运算
1.结合具体事例,理解事件的包含关系及相等关系
2.能结合实例进行随机事件的并、交运算;
3.通过实例,理解随机事件的互斥与对立关系.
学习目标
学习重点 事件的关系与运算的意义
核心素养 数学抽象、逻辑推理、数学运算
一、回顾旧知
1.随机试验
可重复性、可预知性、随机性
2.样本空间、样本点
Ω={ω1,ω2,…,ωn} 写随机试验的样本空间时,
要按照一定的顺序,特别注意题目的关键字,
如“先后”“依次”“放回”“不放回”等.
3.辨析随机事件、必然事件、不可能事件时
要注意看清条件
二、探究新知
请用集合形式表示上述这些事件.
你能发现这些事件之间的关系吗?
B
A
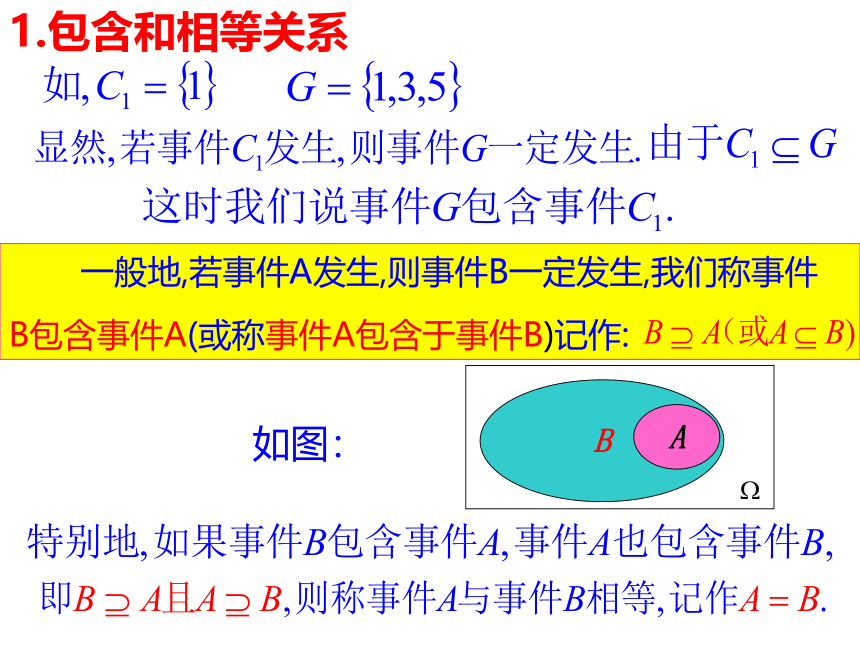
如图:
一般地,若事件A发生,则事件B一定发生,我们称事件
B包含事件A(或称事件A包含于事件B)记作:
1.包含和相等关系
一般地,事件A与事件B至少有一个发生,这样的一个事件中的样本点或者在A中,或者在B中,我们称这个事件为事件A与事件B的并事件(或和事件),记作 .
B
A
如图:
2.并事件(或和事件)
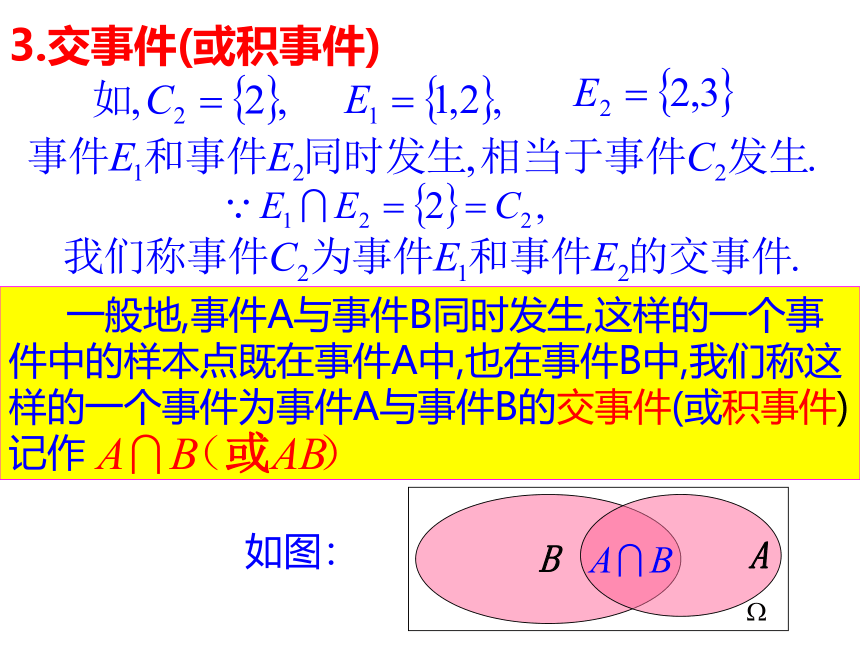
一般地,事件A与事件B同时发生,这样的一个事件中的样本点既在事件A中,也在事件B中,我们称这样的一个事件为事件A与事件B的交事件(或积事件)记作
B
A
如图:
3.交事件(或积事件)
A
B
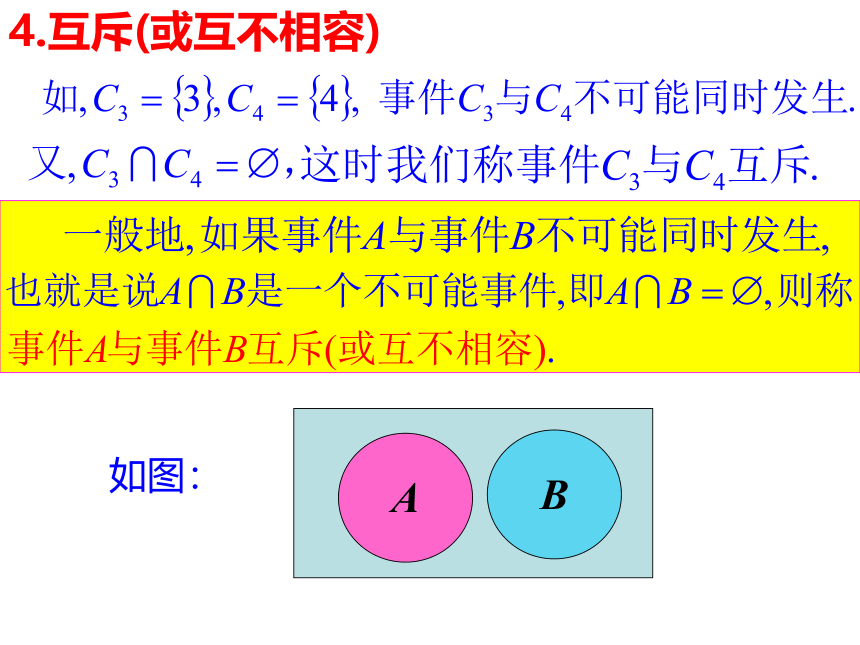
如图:
4.互斥(或互不相容)
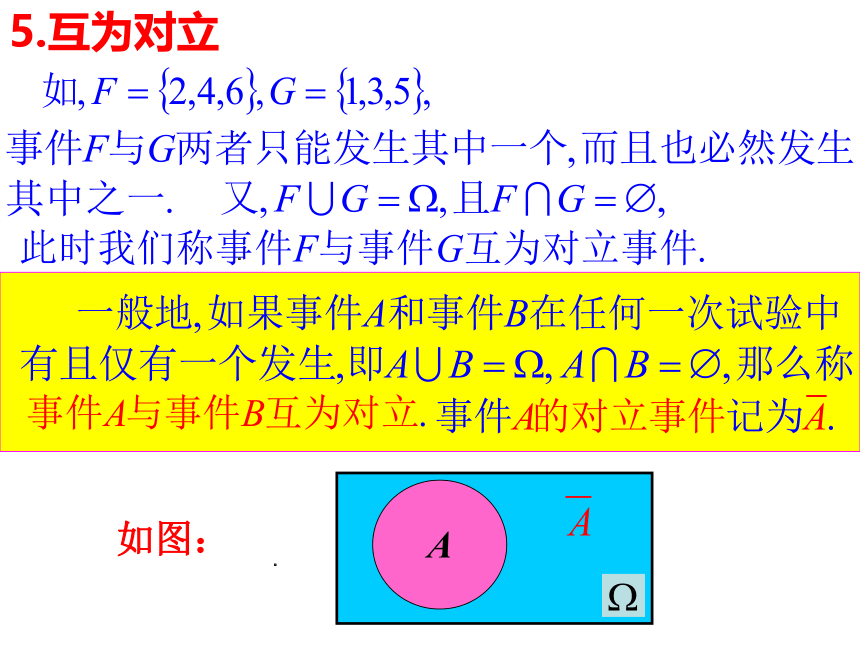
5.互为对立
A
如图:
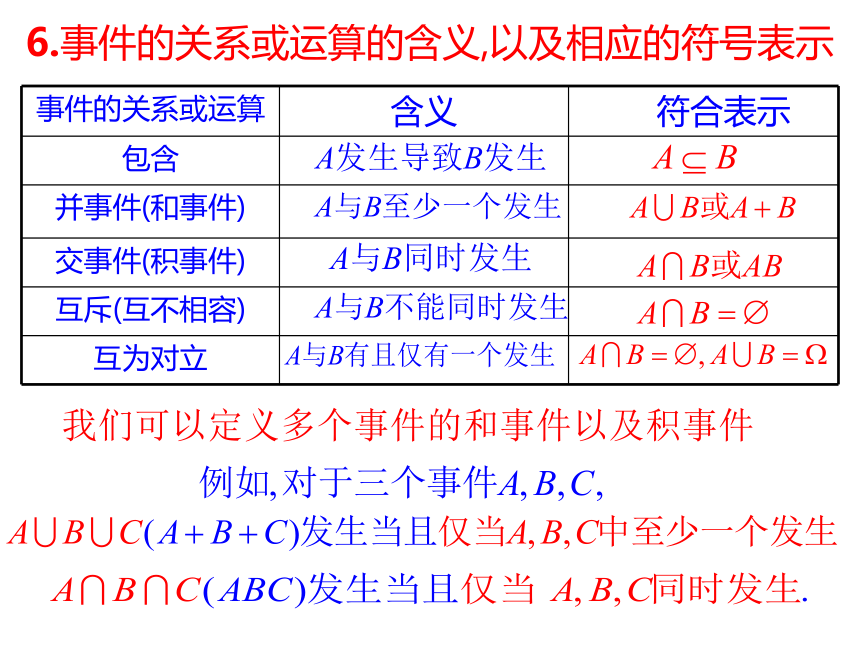
6.事件的关系或运算的含义,以及相应的符号表示
事件的关系或运算 含义 符合表示
包含
并事件(和事件)
交事件(积事件)
互斥(互不相容)
互为对立
三、应用新知
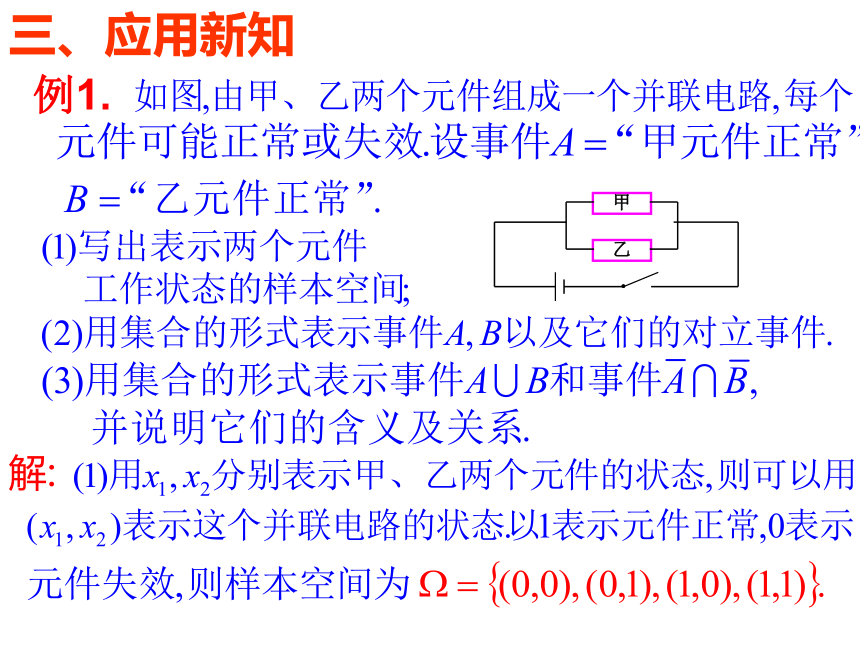
例1.
甲
乙
·
解:
解:
例1.
甲
乙
·
例2.
解:
例2.
解(2)
例2.
解(3)
1、某检查员从一批产品中抽取8件进行检查,观察其中的次品数,记:A ={次品数少于5件};
B ={次品数恰有2件} C ={次品数多于3件};
试写出下列事件的基本事件组成:
A∪ B , A ∩C, B∩ C .
A∪B = A
A∩C ={有4件次品}
B∩C =
课堂练习
2、一个人打靶时连续射击两次,事件“至少有
一次中靶”的互为对立事件是( )
A.至多有一次中靶 B. 两次都中靶
C.只有一次中靶 D.两次都不中靶
D
课堂练习
1、互斥事件是不可能同时发生的两个事件,而对立事件是其中必有一个要发生的互斥事件.因此,对立事件是互斥事件,但互斥事件不一定是对立事件
2、对立事件是对两个事件而言的,而互斥事件是对两个或两个以上事件而言的.
互斥事件与对立事件联系与区别
3、袋中装有白球3个,黑球4个,从中任取3个,是对立事件的为( )
①恰有1个白球和全是白球;
②至少有1个白球和全是黑球;
③至少有1个白球和至少有2个白球;
④至少有1个白球和至少有1个黑球.
A.① B.② C.③ D.④
B
课堂练习
4、袋内红、白、黑球分别为3个、2个、1个,从中任取2个,则互斥而不对立的两个事件是 ( )
A.至少有一个白球;红、黑球各1个
B.至少有一个白球;至少有一个红球
C.恰有一个白球;一个白球一个黑球
D.至少有一个白球;都是白球
A
事件的关系和运算:
(2)并事件(和事件):
(3)交事件(积事件):
(4)互斥事件:
(5)互为对立事件:
(1)包含关系:
且 是必然事件
四、课堂小结
1.某人射击一次,设事件A为“击中环数小于4”,事件B为“击中环数大于4”,事件C为“击中环数不小于4”,事件D为“击中环数大于0且小于4”,则正确的关系是
A.A与B为对立事件 B.B与C互斥
C.C与D为对立事件 D.B与D互斥
1
2
3
4
√
巩固练习
1
2
3
4
在A中,A和B是互斥但不对立事件,故A错误;
在B中,B和C能同时发生,不是互斥事件,故B错误;
在C中,C与D是互斥事件,故C错误;
在D中,B与D为互斥事件,故D正确.
2.在包含10件次品的100件产品中,抽查10件产品,记事件A为“至少有2件次品”,则A的对立事件为
A.至多有2件次品 B.至多有1件次品
C.至多有2件正品 D.至少有2件正品
1
2
3
4
√
至少有2件次品包含2,3,4,5,6,7,8,9,10件次品,共9个样本点,故它的对立事件为含有1或0件次品,即至多有1件次品.
3.(多选)某小组有三名男生和两名女生,从中任选两名去参加比赛,则下列事件是互斥事件的是
A.“恰有一名男生”和“全是男生”
B.“至少有一名男生”和“至少有一名女生”
C.“至少有一名男生”和“全是男生”
D.“至少有一名男生”和“全是女生”
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.如果A,B是互斥事件,那么
√
1
2
3
4
5.从0,1,2,3,4,5中任取两个数字组成一个两位数.事件A表示组成的两位数是偶数,事件B表示组成的两位数中十位数字大于个位数字,则事件A∩B用样本点表示为_________________________.
{10,20,30,40,50,32,42,52,54}
1
2
3
4
从0,1,2,3,4,5中任取两个数字组成一个两位数,所有的样本点为10,12,13,14,15,20,21,23,24,25,30,31,32,34,35,40,41,42,43,45,50,51,52,53,54,共25个,则事件A={10,12,14,20,24,30,32,34,40,42,50,52,54},
事件B={10,20,30,40,50,21,31,41,51,32,42,52,43,53,54},
故事件A∩B用样本点表示为{10,20,30,40,50,32,42,52,54}.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A是互斥事件,恰有一名男生的实质是选出的两人中有一名男生和一名女生,它与全是男生不可能同时发生;
B不是互斥事件,当选出的两人是一男一女时,“至少有一名男生”和“至少有一名女生”同时发生;
C不是互斥事件;
D是互斥事件.
6.从某大学数学系图书室中任选一本书.设A={数学书};B={中文版的书};C={2022年后出版的书}.问:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)在什么条件下有A∩B∩C=A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
在“图书室中所有数学书都是2022年后出版的且为中文版”的条件下才有A∩B∩C=A.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.1.2事件的关系与运算
1.结合具体事例,理解事件的包含关系及相等关系
2.能结合实例进行随机事件的并、交运算;
3.通过实例,理解随机事件的互斥与对立关系.
学习目标
学习重点 事件的关系与运算的意义
核心素养 数学抽象、逻辑推理、数学运算
一、回顾旧知
1.随机试验
可重复性、可预知性、随机性
2.样本空间、样本点
Ω={ω1,ω2,…,ωn} 写随机试验的样本空间时,
要按照一定的顺序,特别注意题目的关键字,
如“先后”“依次”“放回”“不放回”等.
3.辨析随机事件、必然事件、不可能事件时
要注意看清条件
二、探究新知
请用集合形式表示上述这些事件.
你能发现这些事件之间的关系吗?
B
A
如图:
一般地,若事件A发生,则事件B一定发生,我们称事件
B包含事件A(或称事件A包含于事件B)记作:
1.包含和相等关系
一般地,事件A与事件B至少有一个发生,这样的一个事件中的样本点或者在A中,或者在B中,我们称这个事件为事件A与事件B的并事件(或和事件),记作 .
B
A
如图:
2.并事件(或和事件)
一般地,事件A与事件B同时发生,这样的一个事件中的样本点既在事件A中,也在事件B中,我们称这样的一个事件为事件A与事件B的交事件(或积事件)记作
B
A
如图:
3.交事件(或积事件)
A
B
如图:
4.互斥(或互不相容)
5.互为对立
A
如图:
6.事件的关系或运算的含义,以及相应的符号表示
事件的关系或运算 含义 符合表示
包含
并事件(和事件)
交事件(积事件)
互斥(互不相容)
互为对立
三、应用新知
例1.
甲
乙
·
解:
解:
例1.
甲
乙
·
例2.
解:
例2.
解(2)
例2.
解(3)
1、某检查员从一批产品中抽取8件进行检查,观察其中的次品数,记:A ={次品数少于5件};
B ={次品数恰有2件} C ={次品数多于3件};
试写出下列事件的基本事件组成:
A∪ B , A ∩C, B∩ C .
A∪B = A
A∩C ={有4件次品}
B∩C =
课堂练习
2、一个人打靶时连续射击两次,事件“至少有
一次中靶”的互为对立事件是( )
A.至多有一次中靶 B. 两次都中靶
C.只有一次中靶 D.两次都不中靶
D
课堂练习
1、互斥事件是不可能同时发生的两个事件,而对立事件是其中必有一个要发生的互斥事件.因此,对立事件是互斥事件,但互斥事件不一定是对立事件
2、对立事件是对两个事件而言的,而互斥事件是对两个或两个以上事件而言的.
互斥事件与对立事件联系与区别
3、袋中装有白球3个,黑球4个,从中任取3个,是对立事件的为( )
①恰有1个白球和全是白球;
②至少有1个白球和全是黑球;
③至少有1个白球和至少有2个白球;
④至少有1个白球和至少有1个黑球.
A.① B.② C.③ D.④
B
课堂练习
4、袋内红、白、黑球分别为3个、2个、1个,从中任取2个,则互斥而不对立的两个事件是 ( )
A.至少有一个白球;红、黑球各1个
B.至少有一个白球;至少有一个红球
C.恰有一个白球;一个白球一个黑球
D.至少有一个白球;都是白球
A
事件的关系和运算:
(2)并事件(和事件):
(3)交事件(积事件):
(4)互斥事件:
(5)互为对立事件:
(1)包含关系:
且 是必然事件
四、课堂小结
1.某人射击一次,设事件A为“击中环数小于4”,事件B为“击中环数大于4”,事件C为“击中环数不小于4”,事件D为“击中环数大于0且小于4”,则正确的关系是
A.A与B为对立事件 B.B与C互斥
C.C与D为对立事件 D.B与D互斥
1
2
3
4
√
巩固练习
1
2
3
4
在A中,A和B是互斥但不对立事件,故A错误;
在B中,B和C能同时发生,不是互斥事件,故B错误;
在C中,C与D是互斥事件,故C错误;
在D中,B与D为互斥事件,故D正确.
2.在包含10件次品的100件产品中,抽查10件产品,记事件A为“至少有2件次品”,则A的对立事件为
A.至多有2件次品 B.至多有1件次品
C.至多有2件正品 D.至少有2件正品
1
2
3
4
√
至少有2件次品包含2,3,4,5,6,7,8,9,10件次品,共9个样本点,故它的对立事件为含有1或0件次品,即至多有1件次品.
3.(多选)某小组有三名男生和两名女生,从中任选两名去参加比赛,则下列事件是互斥事件的是
A.“恰有一名男生”和“全是男生”
B.“至少有一名男生”和“至少有一名女生”
C.“至少有一名男生”和“全是男生”
D.“至少有一名男生”和“全是女生”
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.如果A,B是互斥事件,那么
√
1
2
3
4
5.从0,1,2,3,4,5中任取两个数字组成一个两位数.事件A表示组成的两位数是偶数,事件B表示组成的两位数中十位数字大于个位数字,则事件A∩B用样本点表示为_________________________.
{10,20,30,40,50,32,42,52,54}
1
2
3
4
从0,1,2,3,4,5中任取两个数字组成一个两位数,所有的样本点为10,12,13,14,15,20,21,23,24,25,30,31,32,34,35,40,41,42,43,45,50,51,52,53,54,共25个,则事件A={10,12,14,20,24,30,32,34,40,42,50,52,54},
事件B={10,20,30,40,50,21,31,41,51,32,42,52,43,53,54},
故事件A∩B用样本点表示为{10,20,30,40,50,32,42,52,54}.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A是互斥事件,恰有一名男生的实质是选出的两人中有一名男生和一名女生,它与全是男生不可能同时发生;
B不是互斥事件,当选出的两人是一男一女时,“至少有一名男生”和“至少有一名女生”同时发生;
C不是互斥事件;
D是互斥事件.
6.从某大学数学系图书室中任选一本书.设A={数学书};B={中文版的书};C={2022年后出版的书}.问:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)在什么条件下有A∩B∩C=A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
在“图书室中所有数学书都是2022年后出版的且为中文版”的条件下才有A∩B∩C=A.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
