有理数的乘方(苏科版)[上学期]

课件15张PPT。
有理数的乘方教学案例设计 （第一课时）

1、理解有理数乘方的意义。
2、知道底数、指数、幂的概念，能进行乘方运算。 学习目标一、创设情境1扣2扣3扣二、数学实验 四、探索新知、培养能力1、? 求__________________的运算叫乘方。乘方运算的结果叫做__________。
2、? 2×2×2×2×2×2记作_______读作________。2叫做_____，6叫做_____。
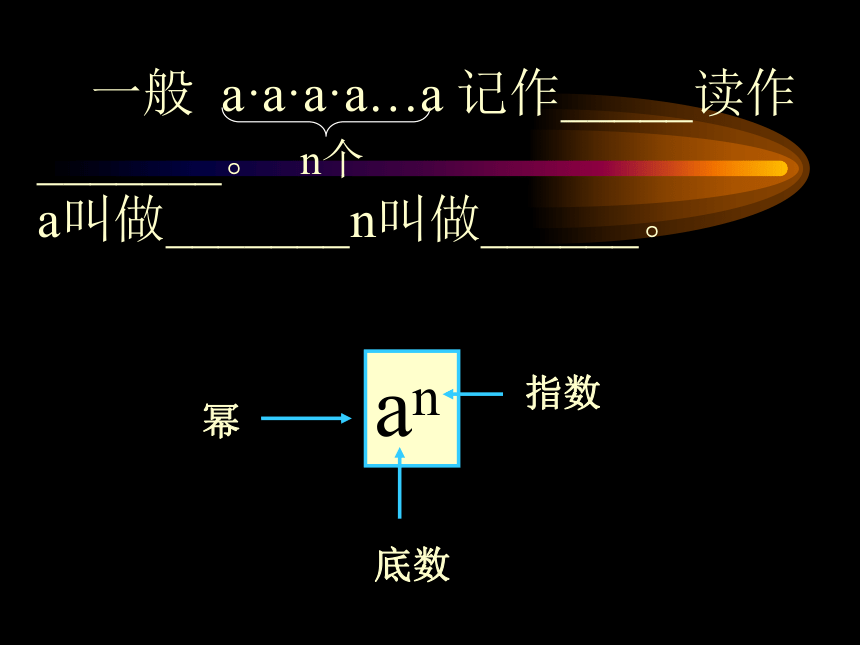
3、 7×7×7记作_______读作_______7叫做________3叫做_____。 一般 a·a·a·a…a 记作_____读作_______。 n个 a叫做_______n叫做______。
an幂底数指数五、研讨范例，提高能力例1、计算
1、①26 ②73 ③(-3)4
④(-4)3 ⑤-34
2、试一试：在横线上填“>”或“<”。
(1) 22___0 23___0 (1/2)5____0
(2) (-2)2__0 (-3)4___0 (-4)6____0
(3) (-2)1 __0 (-3)3___0 (-4)5____0
你能发现正数幂与负数幂的符号特点吗？
正数的任何次幂都是正数
负数的奇数次幂是负数
负数的偶数次幂是正数 大发现例2 计算 (1) (1/2)5
(2) (3/5)3
(3) (-2/3)4

六、试一试（走出教材 拓展延伸）
（一）?? P56练一练1
（二）?? 判断正误（打“√”或“×”）
（1）45=4×5（ ） （2）(-3)4=-34 ( )
（3）( 2/3 )3= 2/27 ( ) （4）26=62（ ）（三）?? 填空（n正整数）
(-1)2=________ (-1)3=________
(-1)4=________ (-1)5=________
(-1)6=________ (-1)7=________
(-1)100=_______ (-1)101=______
(-1)2n=______ (-1)2n-1=_____
1、?你找到的规律是__________________
2、? 若X2=1，则X=___________
1、?你找到的规律是__________________
2、? 若X2=1，则X=___________
（四）拓展延伸
观察图示： +()2+()3+()4+()5=_________



?

?
?（四）观察图示求值：
1/2+(1/2)2+(1/2)3+(1/2)4+(1/2)5=_________
11七、小结1、? 乘方是一种特殊的乘法。
2、? 底数为负数和分数时候应加括号
3、? 关注生活，用数学眼光观察生活中
的实际问题。
4、? “一般——特殊——一般”的数学思 想方法是研究问题的一种常用方法。
?
?八、作业

P58 1、2、6