3.3.1指数函数的概念2022-2023学年高一上学期数学北师大版(2019)必修第一册(word 教案)
文档属性
| 名称 | 3.3.1指数函数的概念2022-2023学年高一上学期数学北师大版(2019)必修第一册(word 教案) |

|
|
| 格式 | docx | ||
| 文件大小 | 496.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-19 00:00:00 | ||
图片预览



文档简介
指数运算与指数函数
3.3.1 指数函数的概念
(1)知识目标:
掌握指数函数的定义;通过指数函数的图象,归纳出指数函数的性质;利用指数函数的性质在不等式、方程问题中的应用.
(2)核心素养目标:
通过指数函数概念、图象和性质的学习,使学生掌握研究函数的一般方法,提高学生的数学抽象和逻辑推理能力.
重难点:
(1) 指数函数的概念;
(2) 指数函数的图象和性质;
(3) 指数函数性质以及利用指数函数的单调性比较实数大小、解不等式等方面的应用.
PPT课件
一、指数函数概念探究
曾经有人断言,一张A4纸,不可能将其对折超过8次,是不是这样呢?
让我们来计算一下,一张标准A4纸,规格为长29.7cm,宽21cm,厚度大约0.01cm,折叠8次,纸的长度变为29.7×cm,厚度变为0.01×cm,这时纸的长度已经小于厚度了,无法再折叠了。
问题1:假设一张厚度0.01cm的A4纸可以无限折叠下去,那么折叠30次的高度大约是多少?折叠50次呢?
师生活动:小组合作讨论,通过对折白纸得出对折次数与所得层数的关系;通过观察绳子的变化,得出剪的次数与剩下的绳长之间的关系.
预设的答案:折叠30次,厚度为0.01×km,大约是12个珠穆朗玛峰的高度了;折叠50次,厚度为0.01×km,约为1.13亿km,地球与太阳的距离约1.5亿km,已接近地球与太阳的距离了。
设计意图:通过探究折纸问题与剪绳问题,导入新课.
问题2:
(1)上面的两个关系式是我们之前学过的某一函数吗?
(2)那它们是函数吗?
(3)有何共同特征?
师生活动:思考问题2,并回答问题,教师引入指数函数的定义,对于给定正数,且时,对于任意的实数,都有唯一确定的与之对应.因此是一个定义在实数集上的函数,称为指数函数.其中是自变量,且.指数函数的定义域为,值域为.
预设的答案:(1)不是学过的函数;(2)是函数,为自变量,为因变量,随的变化而变化;(3)函数解析式都是指数形式,底数为定值,且自变量在指数位置.
设计意图:通过对这三个问题的思考,抽象出指数函数的概念,体现了数学抽象与直观想象的核心素养.
问题3:知道了指数函数的定义,我们能够判断出怎样的函数叫做指数函数吗?
师生活动:教师引导学生从形式定义入手,由指数函数的定义(且)可知,在形式上需从指数,底数,系数三方面说明,学生思考判断函数为指数函数的依据,并发表自己的见解.
预设的答案:
1.指数为单一的
2.大于0且不等于1
3.系数为1,且不含其它项
设计意图:学生通过对形式定义的理解,思考判断函数为指数函数的依据.
问题4:判断下列函数哪些为指数函数?
师生活动:学生独立完成,教师强调判断技巧,判断某些函数是否为指数函数,要看它等价化简之后的形式.
预设的答案: 是指数函数.其它都不是.
设计意图:加深对指数函数的定义的理解,运用判断依据判断哪些函数为指数函数,再次强调判断依据.
问题5:为什么规定底数且?
师生活动:学生思考,以四人为一组讨论,并进行分享.
预设的答案: 若,中不能取像这样的数,此时,函数图象不连续,若,则函数即为,图象过于简单,没有研究的价值.
设计意图:培养学生合作探究以及逻辑推理的能力.
指数函数(且)的图象和性质探究
问题6:如何讨论一个函数的性质,用什么方法?从什么角度?
预设的答案:(用华罗庚的名言“数缺形时少直观,形缺数时难入微,数形结合百般好,割裂分家万事休”引出数形结合法研究函数的性质)
教师:指数函数的图象是怎样的?有怎样的性质呢?首先让我们研究一下底数大于1的情形。
动手实践1:作出指数函数、的图象.
列表、描点、连线得函数的图象如图
… …
… …
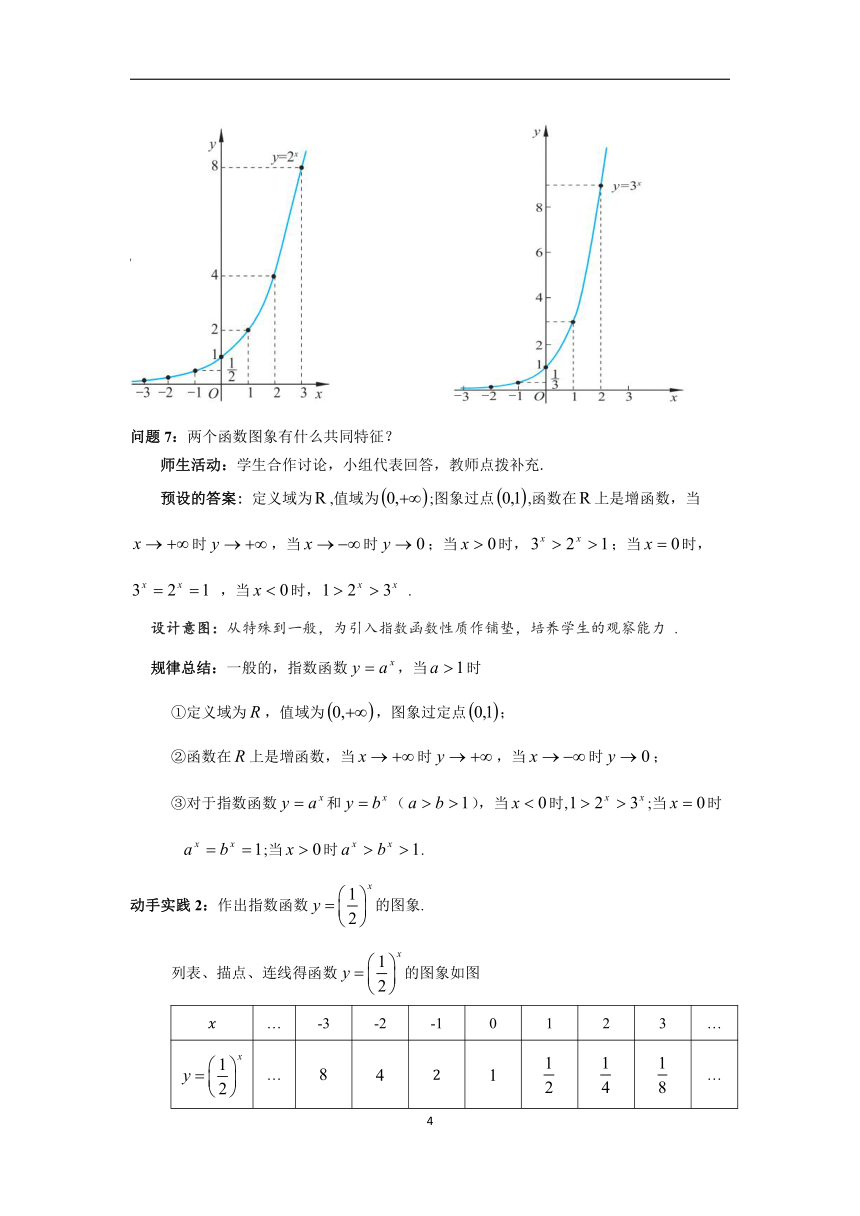
同理可作出指数函数的图象
预设的答案:
问题7:两个函数图象有什么共同特征?
师生活动:学生合作讨论,小组代表回答,教师点拨补充.
预设的答案: 定义域为,值域为;图象过点,函数在上是增函数,当时,当时;当时,;当时, ,当时, .
设计意图:从特殊到一般,为引入指数函数性质作铺垫,培养学生的观察能力 .
规律总结:一般的,指数函数,当时
①定义域为,值域为,图象过定点;
②函数在上是增函数,当时,当时;
③对于指数函数和(),当时,;当时;当时.
动手实践2:作出指数函数的图象.
列表、描点、连线得函数的图象如图
… -3 -2 -1 0 1 2 3 …
… …
同理可作出指数函数的图象
问题8:这两个函数图象有什么共同特征?
师生活动:学生合作讨论,小组代表回答,教师点拨补充.
预设的答案: 定义域为,值域为;图象过点,函数在上是减函数,当时,当时;当时,;当时, ,当时, .
设计意图:从特殊到一般,为引入指数函数性质作铺垫,培养学生的观察能力 .
规律总结:一般的,指数函数,当时
①定义域为,值域为,图象过定点;
②函数在上是增函数,当时,当时;
③对于指数函数和(),当时当时,;当时;
三、初步应用
例1.比较下列各题中两个数的大小:
(1); (2);
师生活动:教师点拨补充,PPT演示解答过程.
预设的答案:由指数函数,当时,函数在上单增
(1),∴
(2),∴
设计意图:熟悉指数函数的性质应用.
例2.(1)求使不等式成立的实数的集合;
(2)已知方程,求实数的值;
师生活动:教师点拨补充,PPT演示解答过程.
预设的答案:
(1)不等式,即,由函数在上单增,得,所以实数的集合为;
(2)方程,即,得,所以.
设计意图:指数函数的性质的灵活应用.
例3.比较下列各题中两个数的大小:
(1) (2);
师生活动:学生类比例1的做法,独立完成,由学生代表上台展示.
预设的答案:由指数函数,当时,函数在上单调递减
设计意图:熟悉指数函数的性质应用.
课堂练习
【课堂练习一】
解不等式;
【课堂练习二】
(2)已知函数(为常数,且)的图象经过点,.
① 求函数的解析式;
②若函数,求的值域.
师生活动:学生独立完成,学生代表在黑板完成解答,教师做出评价.
预设的答案:
(1) 不等式,即
∵函数为增函数,∴,解得
不等式的解集为.
(2) ①图象经过点,得,解得
函数的解析式为
②
,,∴
所以.
设计意图:充分掌握指数函数的性质应用.
四、归纳小结,布置作业
问题10:本节课我们主要学习了哪些内容
师生活动:学生尝试总结,老师适当补充.
预设的答案:
指数函数的定义及特征;指数函数的性质应用.
教材P89,习题3-3:A组第3、4、5、6,B组第1、2、3题.
五、目标检测设计
1.函数,且,则( )
A.4 B.5 C.6 D.8
设计意图:考查指数函数求值.
2.函数则的值为( )
A. B. C.2 D.4
设计意图:考查分段函数中的指数函数求值.
3.函数是指数函数,则a的取值范围是________.
4.已知是指数函数,则实数m的值是___________.
设计意图:3,4考查根据指数函数的形式特征求参数的值.
5.指数函数图像经过点,
(1)求函数的解析式;
(2)解不等式.
设计意图:考查指数函数的定义和简单性质.
参考答案:
1.B
2.C
3.
4.3
5.(1);(2);
7
3.3.1 指数函数的概念
(1)知识目标:
掌握指数函数的定义;通过指数函数的图象,归纳出指数函数的性质;利用指数函数的性质在不等式、方程问题中的应用.
(2)核心素养目标:
通过指数函数概念、图象和性质的学习,使学生掌握研究函数的一般方法,提高学生的数学抽象和逻辑推理能力.
重难点:
(1) 指数函数的概念;
(2) 指数函数的图象和性质;
(3) 指数函数性质以及利用指数函数的单调性比较实数大小、解不等式等方面的应用.
PPT课件
一、指数函数概念探究
曾经有人断言,一张A4纸,不可能将其对折超过8次,是不是这样呢?
让我们来计算一下,一张标准A4纸,规格为长29.7cm,宽21cm,厚度大约0.01cm,折叠8次,纸的长度变为29.7×cm,厚度变为0.01×cm,这时纸的长度已经小于厚度了,无法再折叠了。
问题1:假设一张厚度0.01cm的A4纸可以无限折叠下去,那么折叠30次的高度大约是多少?折叠50次呢?
师生活动:小组合作讨论,通过对折白纸得出对折次数与所得层数的关系;通过观察绳子的变化,得出剪的次数与剩下的绳长之间的关系.
预设的答案:折叠30次,厚度为0.01×km,大约是12个珠穆朗玛峰的高度了;折叠50次,厚度为0.01×km,约为1.13亿km,地球与太阳的距离约1.5亿km,已接近地球与太阳的距离了。
设计意图:通过探究折纸问题与剪绳问题,导入新课.
问题2:
(1)上面的两个关系式是我们之前学过的某一函数吗?
(2)那它们是函数吗?
(3)有何共同特征?
师生活动:思考问题2,并回答问题,教师引入指数函数的定义,对于给定正数,且时,对于任意的实数,都有唯一确定的与之对应.因此是一个定义在实数集上的函数,称为指数函数.其中是自变量,且.指数函数的定义域为,值域为.
预设的答案:(1)不是学过的函数;(2)是函数,为自变量,为因变量,随的变化而变化;(3)函数解析式都是指数形式,底数为定值,且自变量在指数位置.
设计意图:通过对这三个问题的思考,抽象出指数函数的概念,体现了数学抽象与直观想象的核心素养.
问题3:知道了指数函数的定义,我们能够判断出怎样的函数叫做指数函数吗?
师生活动:教师引导学生从形式定义入手,由指数函数的定义(且)可知,在形式上需从指数,底数,系数三方面说明,学生思考判断函数为指数函数的依据,并发表自己的见解.
预设的答案:
1.指数为单一的
2.大于0且不等于1
3.系数为1,且不含其它项
设计意图:学生通过对形式定义的理解,思考判断函数为指数函数的依据.
问题4:判断下列函数哪些为指数函数?
师生活动:学生独立完成,教师强调判断技巧,判断某些函数是否为指数函数,要看它等价化简之后的形式.
预设的答案: 是指数函数.其它都不是.
设计意图:加深对指数函数的定义的理解,运用判断依据判断哪些函数为指数函数,再次强调判断依据.
问题5:为什么规定底数且?
师生活动:学生思考,以四人为一组讨论,并进行分享.
预设的答案: 若,中不能取像这样的数,此时,函数图象不连续,若,则函数即为,图象过于简单,没有研究的价值.
设计意图:培养学生合作探究以及逻辑推理的能力.
指数函数(且)的图象和性质探究
问题6:如何讨论一个函数的性质,用什么方法?从什么角度?
预设的答案:(用华罗庚的名言“数缺形时少直观,形缺数时难入微,数形结合百般好,割裂分家万事休”引出数形结合法研究函数的性质)
教师:指数函数的图象是怎样的?有怎样的性质呢?首先让我们研究一下底数大于1的情形。
动手实践1:作出指数函数、的图象.
列表、描点、连线得函数的图象如图
… …
… …
同理可作出指数函数的图象
预设的答案:
问题7:两个函数图象有什么共同特征?
师生活动:学生合作讨论,小组代表回答,教师点拨补充.
预设的答案: 定义域为,值域为;图象过点,函数在上是增函数,当时,当时;当时,;当时, ,当时, .
设计意图:从特殊到一般,为引入指数函数性质作铺垫,培养学生的观察能力 .
规律总结:一般的,指数函数,当时
①定义域为,值域为,图象过定点;
②函数在上是增函数,当时,当时;
③对于指数函数和(),当时,;当时;当时.
动手实践2:作出指数函数的图象.
列表、描点、连线得函数的图象如图
… -3 -2 -1 0 1 2 3 …
… …
同理可作出指数函数的图象
问题8:这两个函数图象有什么共同特征?
师生活动:学生合作讨论,小组代表回答,教师点拨补充.
预设的答案: 定义域为,值域为;图象过点,函数在上是减函数,当时,当时;当时,;当时, ,当时, .
设计意图:从特殊到一般,为引入指数函数性质作铺垫,培养学生的观察能力 .
规律总结:一般的,指数函数,当时
①定义域为,值域为,图象过定点;
②函数在上是增函数,当时,当时;
③对于指数函数和(),当时当时,;当时;
三、初步应用
例1.比较下列各题中两个数的大小:
(1); (2);
师生活动:教师点拨补充,PPT演示解答过程.
预设的答案:由指数函数,当时,函数在上单增
(1),∴
(2),∴
设计意图:熟悉指数函数的性质应用.
例2.(1)求使不等式成立的实数的集合;
(2)已知方程,求实数的值;
师生活动:教师点拨补充,PPT演示解答过程.
预设的答案:
(1)不等式,即,由函数在上单增,得,所以实数的集合为;
(2)方程,即,得,所以.
设计意图:指数函数的性质的灵活应用.
例3.比较下列各题中两个数的大小:
(1) (2);
师生活动:学生类比例1的做法,独立完成,由学生代表上台展示.
预设的答案:由指数函数,当时,函数在上单调递减
设计意图:熟悉指数函数的性质应用.
课堂练习
【课堂练习一】
解不等式;
【课堂练习二】
(2)已知函数(为常数,且)的图象经过点,.
① 求函数的解析式;
②若函数,求的值域.
师生活动:学生独立完成,学生代表在黑板完成解答,教师做出评价.
预设的答案:
(1) 不等式,即
∵函数为增函数,∴,解得
不等式的解集为.
(2) ①图象经过点,得,解得
函数的解析式为
②
,,∴
所以.
设计意图:充分掌握指数函数的性质应用.
四、归纳小结,布置作业
问题10:本节课我们主要学习了哪些内容
师生活动:学生尝试总结,老师适当补充.
预设的答案:
指数函数的定义及特征;指数函数的性质应用.
教材P89,习题3-3:A组第3、4、5、6,B组第1、2、3题.
五、目标检测设计
1.函数,且,则( )
A.4 B.5 C.6 D.8
设计意图:考查指数函数求值.
2.函数则的值为( )
A. B. C.2 D.4
设计意图:考查分段函数中的指数函数求值.
3.函数是指数函数,则a的取值范围是________.
4.已知是指数函数,则实数m的值是___________.
设计意图:3,4考查根据指数函数的形式特征求参数的值.
5.指数函数图像经过点,
(1)求函数的解析式;
(2)解不等式.
设计意图:考查指数函数的定义和简单性质.
参考答案:
1.B
2.C
3.
4.3
5.(1);(2);
7
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
