【新课标】6.2.1平行四边形的判定 课件(共20张PPT)
文档属性
| 名称 | 【新课标】6.2.1平行四边形的判定 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 14:23:01 | ||
图片预览





文档简介
(共20张PPT)
6.2.1平行四边形的判定
北师版八年级下册
教学目标
1.经历平行四边形的判定定理的探索过程,发展学生的合情推理的能力.
2. 探索并证明平行四边形的判定定理,发展学生的演绎推理的能力.
新知导入
实验室有一块平行四边形的玻璃片(记作:ABCD),在做实验时,小明不小心碰碎了一部分(如图所示),他想配一块一模一样的赔给学校,如果把剩下的玻璃带去玻璃店,他能做到吗?
新知讲解
工具:取四根细木条,其中两根长度相同,另外两根长度也相同
动手:能否合理摆放这四根细木条,使得连接四个顶点后成为平行四边形?
思考:你能说明你得到的四边形是平行四边形吗?
动动手
新知讲解
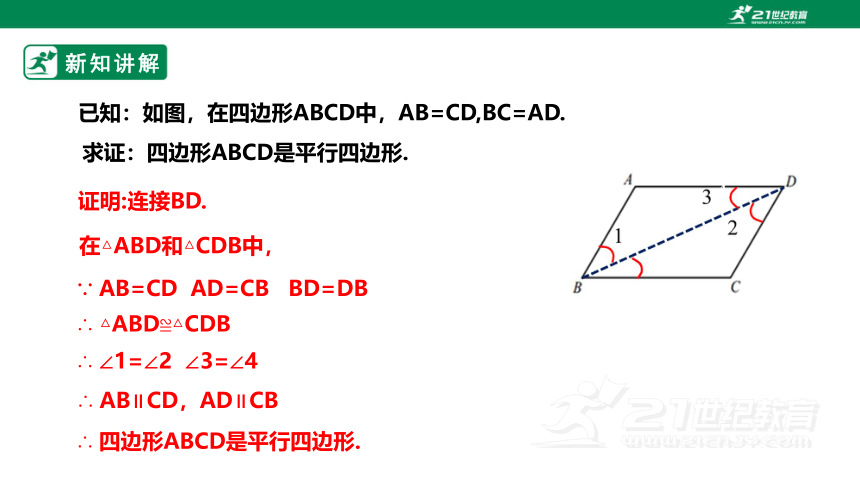
已知:如图,在四边形ABCD中,AB=CD,BC=AD.
∴ 四边形ABCD是平行四边形.
证明:连接BD.
在△ABD和△CDB中,
∵ AB=CD AD=CB BD=DB
∴ △ABD≌△CDB
∴ ∠1=∠2 ∠3=∠4
∴ AB∥CD,AD∥CB
求证:四边形ABCD是平行四边形.
归纳总结
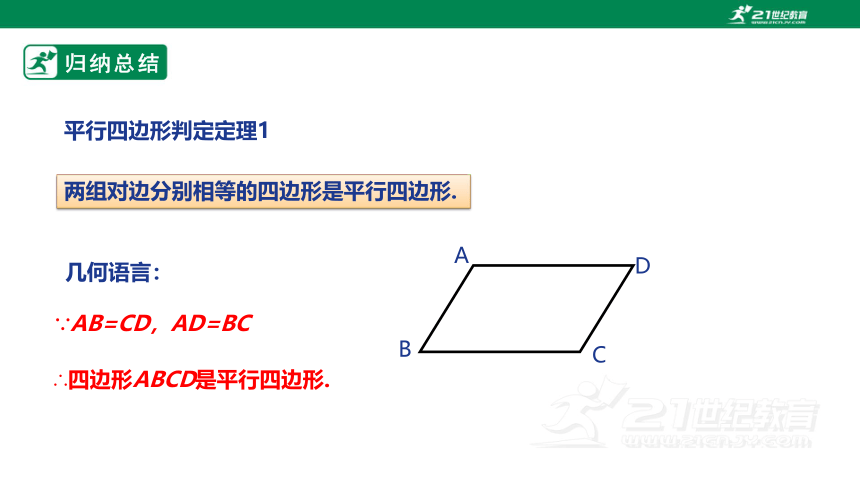
两组对边分别相等的四边形是平行四边形.
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1
B
D
C
A
探究新知
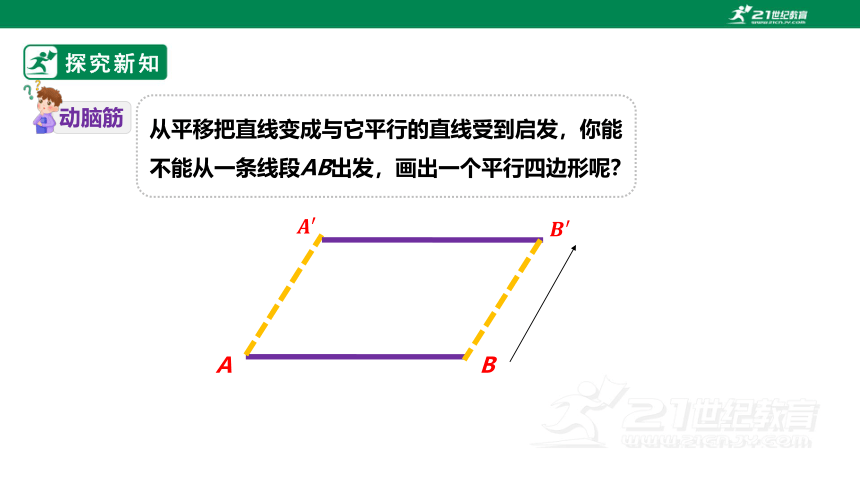
从平移把直线变成与它平行的直线受到启发,你能不能从一条线段AB出发,画出一个平行四边形呢?
B
A
动脑筋
探究新知
将线段AB 沿着如图所给的方向和距离,平移到A′B ′,构成四边形
ABB ′A′.
想一想:这个四边形具备了怎样的特征?
猜想:一组对边平行且相等的四边形是平行四边形.
你能用一句话概括你的发现吗?
探究新知
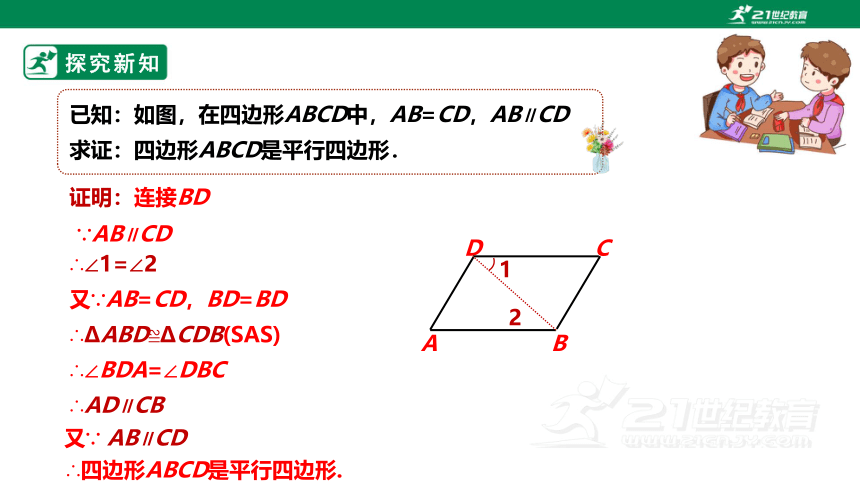
已知:如图,在四边形ABCD中,AB=CD,AB∥CD
求证:四边形ABCD是平行四边形.
B
C
A
D
证明:连接BD
∵AB∥CD
∴∠1=∠2
又∵AB=CD,BD=BD
∴ΔABD≌ΔCDB(SAS)
∴∠BDA=∠DBC
又∵ AB∥CD
∴四边形ABCD是平行四边形.
∴AD∥CB
1
2
归纳总结
一组对边平行且相等的四边形是平行四边形
A
B
C
D
∵AB∥CD, AB=CD.
∴四边形ABCD是平行四边形
几何语言:
平行四边形判定定理2
典例精析
例1、已知:如图,在□ABCD中,点E,F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
∴ ED = FB,ED∥FB.
∴ 四边形 BFDE 是平行四边形(一组对边平行且相等的四边形是平行四边形).
证明:∵ 四边形 ABCD 是平行四边形,
∴ AD = CB(平行四边形的对边相等),
AD ∥ CB(平行四边形的定义).
∵ E,F 分别是 AD 和 CB 的中点,
∴ ED = AD,FB =CB.
练一练
如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,求证:四边形EFNM是平行四边形.
证明:
∵四边形ABCD是平行四边形
∴AD//BC
∵EF=MN
∴四边形EFNM是平行四边形.
课堂练习
1.如图,在四边形ABCD中,点E是BC边的中点,连接DE并延长,交AB的延长线于F点,AB=BF. 添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( )
A.AD=BC B.CD=BF
C.∠A=∠C D.∠F=∠CDE
D
课堂练习
2.四边形的四条边长分别是a,b,c,d,其中a,b为一组对边长,c,d为另一组对边长且a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
A.任意四边形 B.平行四边形
C.对角线相等的四边形 D.对角线垂直的四边形
B
3.已知AD//BC ,要使这个四边形ABCD为平行四边形,需要增加条件 .
AD=BC或AB//CD
课堂练习
4.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
证明:作对角线BD,交AC于点O,
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形.
D
O
A
B
C
E
F
课堂练习
5. 如图,在平行四边形ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,试证明四边形AFCE是平行四边形.
证明:∵在平行四边形ABCD中,
AE、CF分别是∠DAB、 ∠BCD的角平分线
∴∠B=∠D,AB=CD, AD∥BC
∠BAE=∠DCF=∠DAB=∠BCD
∴△ABE≌△CDF(ASA)
∴BE=DF∴AF=CE ∵AF∥CE
∴四边形AFCE是平行四边形
(一组对边平行且相等的四边形是平行四边形)
板书设计
课题:6.2.1平行四边形的判定
1.两组对边分别相等的四边形是平行四边形
2.一组对边平行且相等的四边形是平行四边形
作业布置
【必做题】
教材142页练习题1、2题
【选做题】
教材143页练习题3题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
6.2.1平行四边形的判定
北师版八年级下册
教学目标
1.经历平行四边形的判定定理的探索过程,发展学生的合情推理的能力.
2. 探索并证明平行四边形的判定定理,发展学生的演绎推理的能力.
新知导入
实验室有一块平行四边形的玻璃片(记作:ABCD),在做实验时,小明不小心碰碎了一部分(如图所示),他想配一块一模一样的赔给学校,如果把剩下的玻璃带去玻璃店,他能做到吗?
新知讲解
工具:取四根细木条,其中两根长度相同,另外两根长度也相同
动手:能否合理摆放这四根细木条,使得连接四个顶点后成为平行四边形?
思考:你能说明你得到的四边形是平行四边形吗?
动动手
新知讲解
已知:如图,在四边形ABCD中,AB=CD,BC=AD.
∴ 四边形ABCD是平行四边形.
证明:连接BD.
在△ABD和△CDB中,
∵ AB=CD AD=CB BD=DB
∴ △ABD≌△CDB
∴ ∠1=∠2 ∠3=∠4
∴ AB∥CD,AD∥CB
求证:四边形ABCD是平行四边形.
归纳总结
两组对边分别相等的四边形是平行四边形.
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1
B
D
C
A
探究新知
从平移把直线变成与它平行的直线受到启发,你能不能从一条线段AB出发,画出一个平行四边形呢?
B
A
动脑筋
探究新知
将线段AB 沿着如图所给的方向和距离,平移到A′B ′,构成四边形
ABB ′A′.
想一想:这个四边形具备了怎样的特征?
猜想:一组对边平行且相等的四边形是平行四边形.
你能用一句话概括你的发现吗?
探究新知
已知:如图,在四边形ABCD中,AB=CD,AB∥CD
求证:四边形ABCD是平行四边形.
B
C
A
D
证明:连接BD
∵AB∥CD
∴∠1=∠2
又∵AB=CD,BD=BD
∴ΔABD≌ΔCDB(SAS)
∴∠BDA=∠DBC
又∵ AB∥CD
∴四边形ABCD是平行四边形.
∴AD∥CB
1
2
归纳总结
一组对边平行且相等的四边形是平行四边形
A
B
C
D
∵AB∥CD, AB=CD.
∴四边形ABCD是平行四边形
几何语言:
平行四边形判定定理2
典例精析
例1、已知:如图,在□ABCD中,点E,F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
∴ ED = FB,ED∥FB.
∴ 四边形 BFDE 是平行四边形(一组对边平行且相等的四边形是平行四边形).
证明:∵ 四边形 ABCD 是平行四边形,
∴ AD = CB(平行四边形的对边相等),
AD ∥ CB(平行四边形的定义).
∵ E,F 分别是 AD 和 CB 的中点,
∴ ED = AD,FB =CB.
练一练
如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,求证:四边形EFNM是平行四边形.
证明:
∵四边形ABCD是平行四边形
∴AD//BC
∵EF=MN
∴四边形EFNM是平行四边形.
课堂练习
1.如图,在四边形ABCD中,点E是BC边的中点,连接DE并延长,交AB的延长线于F点,AB=BF. 添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( )
A.AD=BC B.CD=BF
C.∠A=∠C D.∠F=∠CDE
D
课堂练习
2.四边形的四条边长分别是a,b,c,d,其中a,b为一组对边长,c,d为另一组对边长且a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
A.任意四边形 B.平行四边形
C.对角线相等的四边形 D.对角线垂直的四边形
B
3.已知AD//BC ,要使这个四边形ABCD为平行四边形,需要增加条件 .
AD=BC或AB//CD
课堂练习
4.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
证明:作对角线BD,交AC于点O,
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形.
D
O
A
B
C
E
F
课堂练习
5. 如图,在平行四边形ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,试证明四边形AFCE是平行四边形.
证明:∵在平行四边形ABCD中,
AE、CF分别是∠DAB、 ∠BCD的角平分线
∴∠B=∠D,AB=CD, AD∥BC
∠BAE=∠DCF=∠DAB=∠BCD
∴△ABE≌△CDF(ASA)
∴BE=DF∴AF=CE ∵AF∥CE
∴四边形AFCE是平行四边形
(一组对边平行且相等的四边形是平行四边形)
板书设计
课题:6.2.1平行四边形的判定
1.两组对边分别相等的四边形是平行四边形
2.一组对边平行且相等的四边形是平行四边形
作业布置
【必做题】
教材142页练习题1、2题
【选做题】
教材143页练习题3题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
