4.5函数模型的应用(二)第2课时2022-2023学年高一上学期数学人教A版(2019)必修第一册(word教案)
文档属性
| 名称 | 4.5函数模型的应用(二)第2课时2022-2023学年高一上学期数学人教A版(2019)必修第一册(word教案) |

|
|
| 格式 | docx | ||
| 文件大小 | 918.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-19 00:00:00 | ||
图片预览



文档简介
环节四 函数模型的应用(二)第2课时
1.通过热门的实际问题建立数学模型来求解的,经历建模的过程,提升学生的数学素养.
2.能识别三种函数的增长模式不同,合理选择.
3.函数建模思想是重要的思想,让学生不断探索寻求最贴合的函数模型,提升数学抽象能力和建模能力.
教学重点:掌握建模的过程和步骤.
教学难点:掌握函数建模的思想和方法.
PPT.
知识应用
例5 假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
问题1 为了选择出合适的投资方案,我们可以利用什么数学工具比较这三种投资方案的回报情况?
答案:我们可以利用函数工具对这三种投资方案进行比较.可以先建立三种投资方案所对应的函数模型,再通过比较它们的增长情况,为选择投资方案提供依据.
追问1 三种方案的本质是三个不同的函数模型,你能根据题中提供的三种投资方案的描述,分析出其中的常量、变量及其相互关系,并建立三种投资方案所对应的函数模型吗?
答案:三种投资方案每天所得的回报都是随天数的变化而变化的,即每天的回报是关于天数的函数,因此可设第x天所得回报是y元.
方案一每天的回报是固定的40元,可以用函数y=40(x∈N*)进行描述.
方案二每天的回报是递增的,并且第一天的回报是10元,以后每天回报的增加量是10元,可以用函数y=10x(x∈N*)进行描述.
方案三每天的回报也是递增的,并且第一天的回报是0.4元,但以后每天回报的增长率是1,即以后每天的回报都是前一天的1+1=2倍,可以用函数y=0.4×2x-1(x∈N*)进行描述.
追问2 三种方案所对应的三个函数模型有何差异?我们可以通过什么方法对它们增长情况的差异进行分析?
答案:三个模型中,第一个是常数函数,第二个是直线型函数,第三个是指数型函数.要对它们增长情况的差异进行分析,可以通过列表的方式,比较函数值和自变量的变化情况.也可以在同一直角坐标系中画出三个函数的图象,观察图象的变化趋势.
追问3 利用计算器,列出三种方案所对应的三个函数的自变量与函数值,以及函数值增加量的对应值表.并根据对应值表,在同一直角坐标系中,画出三个函数的图象.根据对应值表和函数图象,描述一下三种方案的特点.
答案 完成的对应值表如表1.
表1
x 方案一 方案二 方案三
y 增加量/元 y 增加量/元 y 增加量/元
1 40 10 0.4
2 40 0 20 10 0.8 0.4
3 40 0 30 10 1.6 0.8
4 40 0 40 10 3.2 1.6
5 40 0 50 10 6.4 3.2
6 40 0 60 10 12.8 6.4
7 40 0 70 10 25.6 12.8
8 40 0 80 10 51.2 25.6
9 40 0 90 10 102.4 51.2
10 40 0 100 10 204.8 102.4
… … … … … … …
30 40 0 300 10 214 748 364.8 107 374 182.4
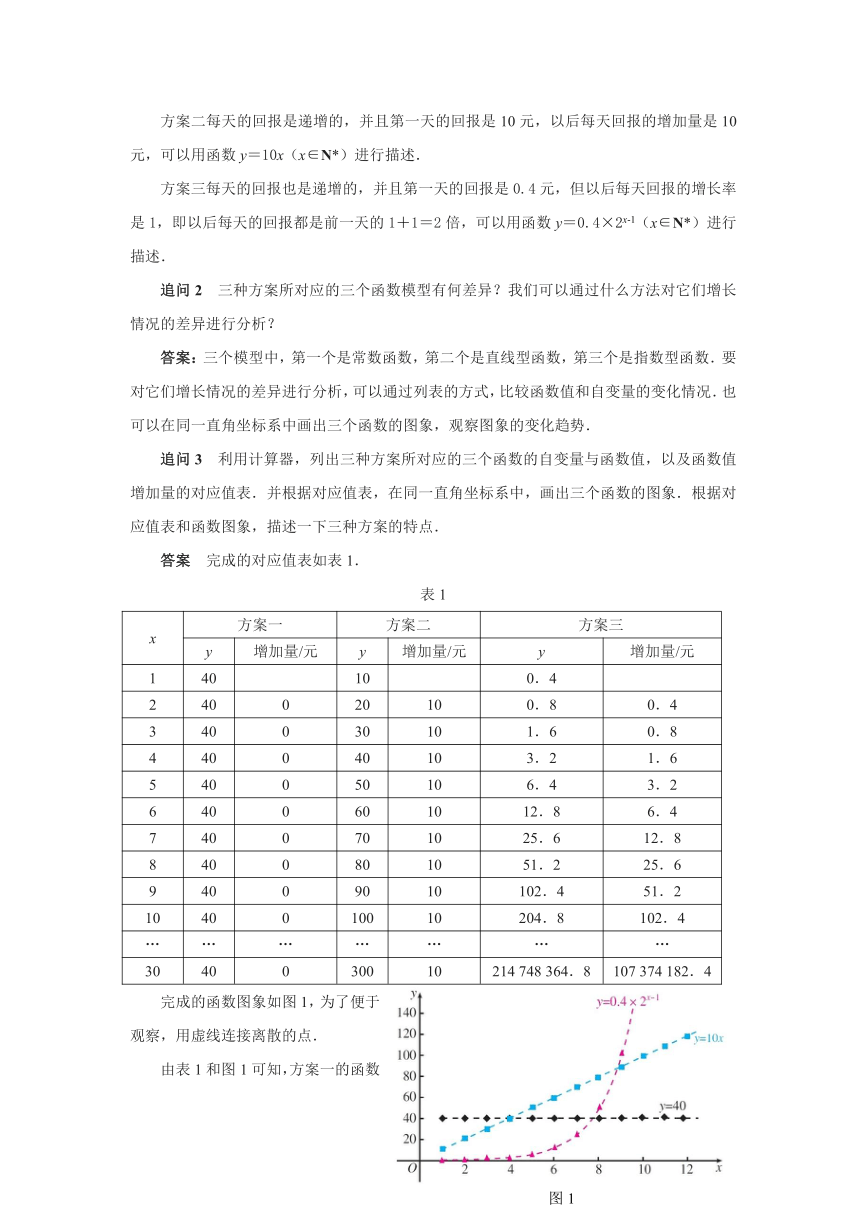
完成的函数图象如图1,为了便于观察,用虚线连接离散的点.
由表1和图1可知,方案一的函数是常函数,方案二、方案三的函数都是增函数,但方案三的函数与方案二的函数的增长情况很不相同.可以看到,尽管方案一、方案二在第一天所得回报分别是方案三的100倍和25倍,但它们的增长量固定不变,而方案三是“指数增长”,其“增长量”是成倍增加的,从第7天开始,方案三比其他两个方案增长得快得多,这种增长速度是方案一、方案二所无法企及的.从每天所得回报看,在第1~3天,方案一最多;在第4天,方案一和方案二一样多,方案三最少;在第5~8天,方案二最多;第9天开始,方案三比其他两个方案所得回报多得多,到第30天,所回报已超过2亿元.
问题2 根据上一问中,对每天的回报数的分析,是否应作出这样的选择:投资5天以下选方案一,投资5~8天选方案二,投资8天以上选方案三?
答案:计算每天回报的增加量(或增长率)是对数据的基本处理方法,虽然根据数表和图象都可以直观看出三种函数模型的增长差异,但要具体到投资的天数,回报的增加量还不足以作为选择投资方案的依据.因为无论是每天的回报,还是每天回报的增加量,都只能反映出一天或者相比于前一天的回报情况,并不能反映出投资的总回报,所以不应这样选择投资方案.
追问 如果不应该这样选择投资方案,那么还应该如何分析三种方案所对应的三个函数模型,进行方案的选择?
答案:投资方案的选择,应该考虑投资一定天数后,总的回报数,因此需要逐天计算累计的回报数.通过利用计算器计算,列出三种方案累计的回报数如表2.
表2
方案 天数
1 2 3 4 5 6 7 8 9 10 11
一 40 80 120 160 200 240 280 320 360 400 440
二 10 30 60 100 150 210 280 360 450 550 660
三 0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4 409.2 818.8
因此,投资1~6天,应选择方案一;投资7天,应选择方案一或方案二;投资8~10天,应选择方案二;投资11天(含11天)以上,则应选择方案三.
例6 某公司为了实现1 000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:,,,其中哪个模型能符合公司的要求?
问题3 根据题目条件,你认为应该如何选择符合公司要求的函数模型?
答案:三种函数模型都是从数学语言的角度,描述了奖金y随销售利润x的变化情况.因此要选择出符合公司要求的函数模型,应当将公司要求也用数学语言进行描述,然后在该要求下,判断三种函数模型是否满足要求,进行选择.
追问 根据题中给出的条件,你能将公司对奖金的要求,转化为用数学语言描述的要求吗?
答案:由于公司总的利润目标为1 000万元,所以销售人员的销售利润一般不会超过公司总的利润.于是只需要在区间上,寻找并验证所选函数是否满足两条要求:第一,奖金总数不超过5万元,即函数的最大值不大于5,;第二,奖金不超过利润的25%,即函数值不超过自变量的0.25倍,.
问题4 函数图象能直观反映函数的性质特征,从而可以直观判断函数模型是否符合公司的要求.为此,你能否在同一直角坐标系中画出函数图象,并根据第一个要求,在同一直角坐标系中再把函数的图象画出,然后通过观察作出初步的判断吗?
答案:利用信息技术在同一直角坐标系中画出函数,,,的图象,画好的函数图象如图2.
观察图象,在区间上,模型,的图象都有一部分在直线的上方,只有模型的图象始终在的下方,这说明只有按模型进行奖励时才符合公司的第一个要求.
追问 为了确认上述判断,我们需要通过具体的计算,确定哪个模型能满足第一个要求,即奖金数不超过5万元,也即.你能结合三个模型所对应的三个函数的性质,计算并判断出它们在区间上,是否满足吗?
答案:对于模型,它在区间上单调递增,而且当时,,因此,当时,,所以该模型不符合要求.
对于模型,由函数图象,并利用信息技术,可知在区间内有一个点x0满足,由于它在区间上单调递增,因此当时,,所以该模型也不符合要求.
对于模型,它在区间上单调递增,而且当时,,所以它符合奖金总数不超过5万元的要求.
问题5 我们已经判断出符合第一个要求的模型只有,还需要进一步判断,按该模型奖励时,奖金是否不超过利润的25%,即当时,是否有,即成立.你认为可以用什么方法判断?
答案:由于和分别为对数型函数和直线型函数,它们在上都是单调递增的,但是它们的增长速度不同.由“4.4.3不同函数增长的差异”可知,的增长速度要比慢得多,所以可以构造函数,在时,观察函数图象的变化趋势,然后再通过定量的计算进行判断是否有.
追问 在直角坐标系中画出函数在区间上的图象.观察图象,然后通过计算判断,在区间上是否有?
答案:利用信息技术画出函数,的图象如图3.
由图象可知函数在区间上单调递减,因此
,
即
.
所以,当时,,说明按模型奖励,奖金不会超过利润的25%.
综上所述,模型确实能符合公司要求.
(二)课堂练习
1.某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y(万公顷)关于年数x(年)的函数关系较为近似的是( )
A.y=0.2x B.y=(x2+2x)
C.y= D.y=0.2+log16x
解:因为三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,可以看出来不是线性增加,故选项A不符合题意;
对于选项B:把x=1,2,3分别代入解析式中,得y=0.3,0.8,1.5,函数值与实际数值相差较大;
对于选项C:把x=1,2,3分别代入解析式中,得y=0.2,0.4,0.8,函数值与实际数值完全吻合或相差无几;
对于选项D:把x=1代入解析式中,得y=0.2;把x=2代入解析式中,得y=0.2+log162=0.45;把x=3代入解析式中,得y=0.2+log163=0.2+log23<0.2+log24=0.7,与选项C相比,选项C更近似,
故选:C.
2.噪声是指发声体做无规则振动时发出的声音.声音由物体的振动产生,以波的形式在一定的介质(如固体 液体 气体)中进行传播.噪声不但会对听力造成损伤,也对人们的生活工作有所干扰,还能诱发多种致癌致命的疾病.科学家经过大量的分析发现:声音强度D(分贝)与声音能量I(W/cm2)之间存在函数关系.经测定,数据如下表:
声音能量 10-13 10-12 ×10-12 ×10-12 ×10-12 ×10-12
声音强度D 30 40 42.7875 44.4716 45.6820 46.6276
为了描述声音强度D(分贝)与声音能量I(W/cm2)之间的函数关系,现有以下两种模型供选择:D=KI+B,D=MlgI+N.
(1)选出你认为符合实际的函数模型,简单叙述理由,并写出相应的解析式;
(2)对于人的耳朵,(40,60]分贝的声音比较适宜室内谈话,(60,70]分贝的声音比较适宜室外谈话.试问声音能量在什么范围时适合人与人交流谈话?
解:(1)选择D=MlgI+N.
原因:当自变量的取值为10-12,×10-12,×10-12,×10-12,×10-12时,
发现自变量增加量为常数×10-12时,但函数增加量不是常数,
所以不选择一次函数,而选择D=MlgI+N.
由已知可得:,
即,解之得,
所以解析式为D=10lgI+160.
(2)由已知可得:当40<D≤70时,适合人与人交流谈话,所以40<10lgI+160≤70,
即:-120<10lgI≤-90,
即:-12<lgI≤-9,所以10-12<I≤10-9.
所以当声音能量I∈(10-12,10-9]时,适合人与人交流谈话.
环节三、归纳总结
问题6 (1)通过解答以上两道例题的实际问题,并结合教科书中的例3和例4,你能归纳出建立函数模型解决实际问题的基本过程吗?
(2)回顾本单元的内容,你能用思维导图梳理本单元的研究内容和方法吗?
答案:(1)用函数建立数学模型解决实际问题的基本过程如下图5:
这一过程包括分析和理解实际问题的增长情况(是“对数增长”“直线上升”还是“指数爆炸”);根据增长情况选择函数类型构建数学模型,将实际问题化归为数学问题;通过运算、推理求解函数模型;用得到的函数模型描述实际问题的变化规律,解决有关问题.在这一过程中,往往需要利用信息技术帮助画图、运算等.
(2)本单元研究内容和方法的思维导图如图6:
本类资源
探究式教学(Hands-on Inquiry Based Learning),又称“做中学”、发现法、研究法,是指学生在学习概念和原理时,教师只是给他们一些事例和问题,让学生自己通过阅读、观察、实验、思考、讨论、听讲等途径去主动探究,自行发现并掌握相应的原理和结论的一种方法。它的指导思想是在教师的指导下,以学生为主体,让学生自觉地、主动地探索,掌握认识和解决问题的方法和步骤,研究客观事物的属性,发现事物发展的起因和事物内部的联系,从中找出规律,形成概念,建立自己的认知模型和学习方法架构。可见,在探究式教学的过程中,学生的主体地位、主动能力都得到了加强。
本类专题资源涵盖了小学、中学常见的数学探究,通过交互动画的形式,展示了定理推导、方法总结、规律探究、问题解决的过程。直观形象、生动有趣,培养学习兴趣,提升教学效率。
1.通过热门的实际问题建立数学模型来求解的,经历建模的过程,提升学生的数学素养.
2.能识别三种函数的增长模式不同,合理选择.
3.函数建模思想是重要的思想,让学生不断探索寻求最贴合的函数模型,提升数学抽象能力和建模能力.
教学重点:掌握建模的过程和步骤.
教学难点:掌握函数建模的思想和方法.
PPT.
知识应用
例5 假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
问题1 为了选择出合适的投资方案,我们可以利用什么数学工具比较这三种投资方案的回报情况?
答案:我们可以利用函数工具对这三种投资方案进行比较.可以先建立三种投资方案所对应的函数模型,再通过比较它们的增长情况,为选择投资方案提供依据.
追问1 三种方案的本质是三个不同的函数模型,你能根据题中提供的三种投资方案的描述,分析出其中的常量、变量及其相互关系,并建立三种投资方案所对应的函数模型吗?
答案:三种投资方案每天所得的回报都是随天数的变化而变化的,即每天的回报是关于天数的函数,因此可设第x天所得回报是y元.
方案一每天的回报是固定的40元,可以用函数y=40(x∈N*)进行描述.
方案二每天的回报是递增的,并且第一天的回报是10元,以后每天回报的增加量是10元,可以用函数y=10x(x∈N*)进行描述.
方案三每天的回报也是递增的,并且第一天的回报是0.4元,但以后每天回报的增长率是1,即以后每天的回报都是前一天的1+1=2倍,可以用函数y=0.4×2x-1(x∈N*)进行描述.
追问2 三种方案所对应的三个函数模型有何差异?我们可以通过什么方法对它们增长情况的差异进行分析?
答案:三个模型中,第一个是常数函数,第二个是直线型函数,第三个是指数型函数.要对它们增长情况的差异进行分析,可以通过列表的方式,比较函数值和自变量的变化情况.也可以在同一直角坐标系中画出三个函数的图象,观察图象的变化趋势.
追问3 利用计算器,列出三种方案所对应的三个函数的自变量与函数值,以及函数值增加量的对应值表.并根据对应值表,在同一直角坐标系中,画出三个函数的图象.根据对应值表和函数图象,描述一下三种方案的特点.
答案 完成的对应值表如表1.
表1
x 方案一 方案二 方案三
y 增加量/元 y 增加量/元 y 增加量/元
1 40 10 0.4
2 40 0 20 10 0.8 0.4
3 40 0 30 10 1.6 0.8
4 40 0 40 10 3.2 1.6
5 40 0 50 10 6.4 3.2
6 40 0 60 10 12.8 6.4
7 40 0 70 10 25.6 12.8
8 40 0 80 10 51.2 25.6
9 40 0 90 10 102.4 51.2
10 40 0 100 10 204.8 102.4
… … … … … … …
30 40 0 300 10 214 748 364.8 107 374 182.4
完成的函数图象如图1,为了便于观察,用虚线连接离散的点.
由表1和图1可知,方案一的函数是常函数,方案二、方案三的函数都是增函数,但方案三的函数与方案二的函数的增长情况很不相同.可以看到,尽管方案一、方案二在第一天所得回报分别是方案三的100倍和25倍,但它们的增长量固定不变,而方案三是“指数增长”,其“增长量”是成倍增加的,从第7天开始,方案三比其他两个方案增长得快得多,这种增长速度是方案一、方案二所无法企及的.从每天所得回报看,在第1~3天,方案一最多;在第4天,方案一和方案二一样多,方案三最少;在第5~8天,方案二最多;第9天开始,方案三比其他两个方案所得回报多得多,到第30天,所回报已超过2亿元.
问题2 根据上一问中,对每天的回报数的分析,是否应作出这样的选择:投资5天以下选方案一,投资5~8天选方案二,投资8天以上选方案三?
答案:计算每天回报的增加量(或增长率)是对数据的基本处理方法,虽然根据数表和图象都可以直观看出三种函数模型的增长差异,但要具体到投资的天数,回报的增加量还不足以作为选择投资方案的依据.因为无论是每天的回报,还是每天回报的增加量,都只能反映出一天或者相比于前一天的回报情况,并不能反映出投资的总回报,所以不应这样选择投资方案.
追问 如果不应该这样选择投资方案,那么还应该如何分析三种方案所对应的三个函数模型,进行方案的选择?
答案:投资方案的选择,应该考虑投资一定天数后,总的回报数,因此需要逐天计算累计的回报数.通过利用计算器计算,列出三种方案累计的回报数如表2.
表2
方案 天数
1 2 3 4 5 6 7 8 9 10 11
一 40 80 120 160 200 240 280 320 360 400 440
二 10 30 60 100 150 210 280 360 450 550 660
三 0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4 409.2 818.8
因此,投资1~6天,应选择方案一;投资7天,应选择方案一或方案二;投资8~10天,应选择方案二;投资11天(含11天)以上,则应选择方案三.
例6 某公司为了实现1 000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:,,,其中哪个模型能符合公司的要求?
问题3 根据题目条件,你认为应该如何选择符合公司要求的函数模型?
答案:三种函数模型都是从数学语言的角度,描述了奖金y随销售利润x的变化情况.因此要选择出符合公司要求的函数模型,应当将公司要求也用数学语言进行描述,然后在该要求下,判断三种函数模型是否满足要求,进行选择.
追问 根据题中给出的条件,你能将公司对奖金的要求,转化为用数学语言描述的要求吗?
答案:由于公司总的利润目标为1 000万元,所以销售人员的销售利润一般不会超过公司总的利润.于是只需要在区间上,寻找并验证所选函数是否满足两条要求:第一,奖金总数不超过5万元,即函数的最大值不大于5,;第二,奖金不超过利润的25%,即函数值不超过自变量的0.25倍,.
问题4 函数图象能直观反映函数的性质特征,从而可以直观判断函数模型是否符合公司的要求.为此,你能否在同一直角坐标系中画出函数图象,并根据第一个要求,在同一直角坐标系中再把函数的图象画出,然后通过观察作出初步的判断吗?
答案:利用信息技术在同一直角坐标系中画出函数,,,的图象,画好的函数图象如图2.
观察图象,在区间上,模型,的图象都有一部分在直线的上方,只有模型的图象始终在的下方,这说明只有按模型进行奖励时才符合公司的第一个要求.
追问 为了确认上述判断,我们需要通过具体的计算,确定哪个模型能满足第一个要求,即奖金数不超过5万元,也即.你能结合三个模型所对应的三个函数的性质,计算并判断出它们在区间上,是否满足吗?
答案:对于模型,它在区间上单调递增,而且当时,,因此,当时,,所以该模型不符合要求.
对于模型,由函数图象,并利用信息技术,可知在区间内有一个点x0满足,由于它在区间上单调递增,因此当时,,所以该模型也不符合要求.
对于模型,它在区间上单调递增,而且当时,,所以它符合奖金总数不超过5万元的要求.
问题5 我们已经判断出符合第一个要求的模型只有,还需要进一步判断,按该模型奖励时,奖金是否不超过利润的25%,即当时,是否有,即成立.你认为可以用什么方法判断?
答案:由于和分别为对数型函数和直线型函数,它们在上都是单调递增的,但是它们的增长速度不同.由“4.4.3不同函数增长的差异”可知,的增长速度要比慢得多,所以可以构造函数,在时,观察函数图象的变化趋势,然后再通过定量的计算进行判断是否有.
追问 在直角坐标系中画出函数在区间上的图象.观察图象,然后通过计算判断,在区间上是否有?
答案:利用信息技术画出函数,的图象如图3.
由图象可知函数在区间上单调递减,因此
,
即
.
所以,当时,,说明按模型奖励,奖金不会超过利润的25%.
综上所述,模型确实能符合公司要求.
(二)课堂练习
1.某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y(万公顷)关于年数x(年)的函数关系较为近似的是( )
A.y=0.2x B.y=(x2+2x)
C.y= D.y=0.2+log16x
解:因为三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,可以看出来不是线性增加,故选项A不符合题意;
对于选项B:把x=1,2,3分别代入解析式中,得y=0.3,0.8,1.5,函数值与实际数值相差较大;
对于选项C:把x=1,2,3分别代入解析式中,得y=0.2,0.4,0.8,函数值与实际数值完全吻合或相差无几;
对于选项D:把x=1代入解析式中,得y=0.2;把x=2代入解析式中,得y=0.2+log162=0.45;把x=3代入解析式中,得y=0.2+log163=0.2+log23<0.2+log24=0.7,与选项C相比,选项C更近似,
故选:C.
2.噪声是指发声体做无规则振动时发出的声音.声音由物体的振动产生,以波的形式在一定的介质(如固体 液体 气体)中进行传播.噪声不但会对听力造成损伤,也对人们的生活工作有所干扰,还能诱发多种致癌致命的疾病.科学家经过大量的分析发现:声音强度D(分贝)与声音能量I(W/cm2)之间存在函数关系.经测定,数据如下表:
声音能量 10-13 10-12 ×10-12 ×10-12 ×10-12 ×10-12
声音强度D 30 40 42.7875 44.4716 45.6820 46.6276
为了描述声音强度D(分贝)与声音能量I(W/cm2)之间的函数关系,现有以下两种模型供选择:D=KI+B,D=MlgI+N.
(1)选出你认为符合实际的函数模型,简单叙述理由,并写出相应的解析式;
(2)对于人的耳朵,(40,60]分贝的声音比较适宜室内谈话,(60,70]分贝的声音比较适宜室外谈话.试问声音能量在什么范围时适合人与人交流谈话?
解:(1)选择D=MlgI+N.
原因:当自变量的取值为10-12,×10-12,×10-12,×10-12,×10-12时,
发现自变量增加量为常数×10-12时,但函数增加量不是常数,
所以不选择一次函数,而选择D=MlgI+N.
由已知可得:,
即,解之得,
所以解析式为D=10lgI+160.
(2)由已知可得:当40<D≤70时,适合人与人交流谈话,所以40<10lgI+160≤70,
即:-120<10lgI≤-90,
即:-12<lgI≤-9,所以10-12<I≤10-9.
所以当声音能量I∈(10-12,10-9]时,适合人与人交流谈话.
环节三、归纳总结
问题6 (1)通过解答以上两道例题的实际问题,并结合教科书中的例3和例4,你能归纳出建立函数模型解决实际问题的基本过程吗?
(2)回顾本单元的内容,你能用思维导图梳理本单元的研究内容和方法吗?
答案:(1)用函数建立数学模型解决实际问题的基本过程如下图5:
这一过程包括分析和理解实际问题的增长情况(是“对数增长”“直线上升”还是“指数爆炸”);根据增长情况选择函数类型构建数学模型,将实际问题化归为数学问题;通过运算、推理求解函数模型;用得到的函数模型描述实际问题的变化规律,解决有关问题.在这一过程中,往往需要利用信息技术帮助画图、运算等.
(2)本单元研究内容和方法的思维导图如图6:
本类资源
探究式教学(Hands-on Inquiry Based Learning),又称“做中学”、发现法、研究法,是指学生在学习概念和原理时,教师只是给他们一些事例和问题,让学生自己通过阅读、观察、实验、思考、讨论、听讲等途径去主动探究,自行发现并掌握相应的原理和结论的一种方法。它的指导思想是在教师的指导下,以学生为主体,让学生自觉地、主动地探索,掌握认识和解决问题的方法和步骤,研究客观事物的属性,发现事物发展的起因和事物内部的联系,从中找出规律,形成概念,建立自己的认知模型和学习方法架构。可见,在探究式教学的过程中,学生的主体地位、主动能力都得到了加强。
本类专题资源涵盖了小学、中学常见的数学探究,通过交互动画的形式,展示了定理推导、方法总结、规律探究、问题解决的过程。直观形象、生动有趣,培养学习兴趣,提升教学效率。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
