人教A版(2019)必修二 10.2 事件的相互独立性 (课件38张)
文档属性
| 名称 | 人教A版(2019)必修二 10.2 事件的相互独立性 (课件38张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-19 00:00:00 | ||
图片预览











文档简介
(共38张PPT)
10.2 事件的相互独立性
学习目标
1.了解两个随机事件相互独立的含义;
2.结合古典概型,利用独立性计算概率;
3.能利用相互独立性事件同时发生的概率公式解决一些简单的实际问题.
核心素养
数学抽象、数学建模、逻辑推理。
温故知新
温故知新
新课导入
前面我们研究过互斥事件、对立事件的概率性质,还研究过和事件的概率计算方法.
对于积事件的概率,你能提出什么值得研究的问题吗? 我们知道,积事件AB就是事件A与事件B同时发生. 因此,积事件AB发生的概率一定与事件A,B发生的概率有关. 那么,这种关系会是怎样的呢?
下面我们来讨论一类与积事件有关的特殊问题.
探究1
下面两个随机试验各定义了一对随机事件A和B,你觉得事件A发生与否会影响事件B发生的概率吗?
试验1:分别抛掷两枚质地均匀的硬币,A= “第一枚硬币正面朝上”,B=“第二枚硬币反面朝上”.
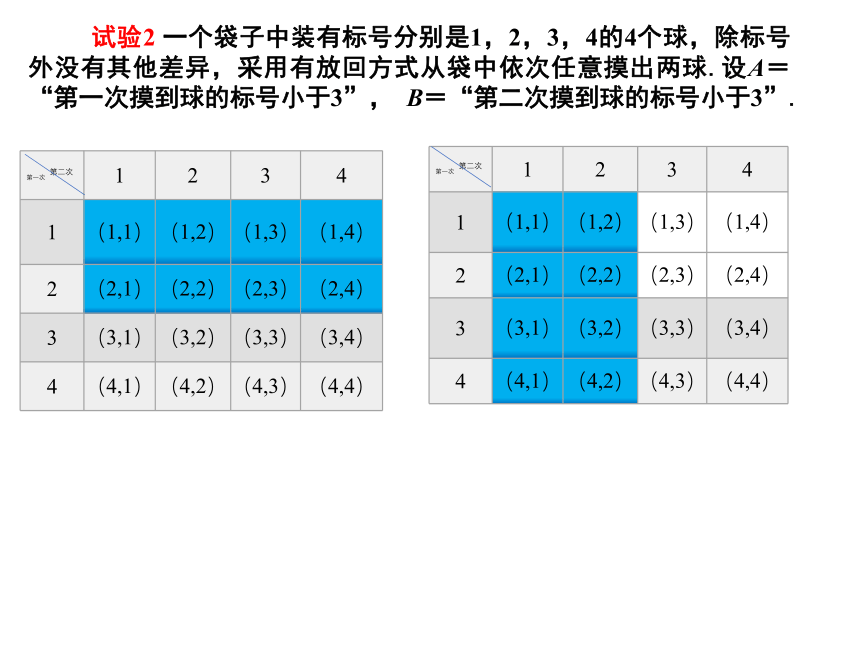
试验2: —个袋子中装有标号分别是1, 2, 3, 4的4个球,除标号外没有其它差异. 采用有放回方式从袋中依次任意摸出两球. A= “第一次摸到球的标号小于3”,B = “第二次摸到球的标号小于3”.
分别计算P(A),P(B),P(AB),你有什么发现?
新课讲解
因为两枚硬币分别拋掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率.
下面两个随机试验各定义了一对随机事件A和B,你觉得事件A发生与否会影响事件B发生的概率吗?
试验1:分别抛掷两枚质地均匀的硬币,A= “第一枚硬币正面朝上”,B=“第二枚硬币反面朝上”.
计算P(A),P(B),P(AB),你有什么发现?
新课讲解
下面两个随机试验各定义了一对随机事件A和B,你觉得事件A发生与否会影响事件B发生的概率吗?
试验1:分别抛掷两枚质地均匀的硬币,A= “第一枚硬币正面朝上”,B=“第二枚硬币反面朝上”.
计算P(A),P(B),P(AB),你有什么发现?
用1表示硬币“正面朝上”,用0表示硬币“反面朝上”,则样本空间为Ω ={(1, 1), (1, 0), (0, 1), (0, 0)}, 包含 4 个等可能的样本点. 而 A ={(1, 1), (1, 0)}, B={(1, 0), (0, 0)}, 所以AB={(1, 0)}. 由古典概型概率计算公式,得
P(A)=P(B)= , P(AB)= . 于是P(AB)=P(A)P(B).
积事件AB的概率P(AB)恰好等于P(A)与P(B)的乘积.
试验2 一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异,采用有放回方式从袋中依次任意摸出两球.设A=“第一次摸到球的标号小于3”, B=“第二次摸到球的标号小于3”.
第一次 第二次 1 2 3 4
1 (1,1) (1,2) (1,3) (1,4)
2 (2,1) (2,2) (2,3) (2,4)
3 (3,1) (3,2) (3,3) (3,4)
4 (4,1) (4,2) (4,3) (4,4)
第一次 第二次 1 2 3 4
1 (1,1) (1,2) (1,3) (1,4)
2 (2,1) (2,2) (2,3) (2,4)
3 (3,1) (3,2) (3,3) (3,4)
4 (4,1) (4,2) (4,3) (4,4)
试验2 一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异,采用有放回方式从袋中依次任意摸出两球.设A=“第一次摸到球的标号小于3”, B=“第二次摸到球的标号小于3”.
即 积事件AB的概率P(AB)恰好等于P(A)与P(B)的乘积.
从上述两个试验的共性中得到启发,我们引入这种事件关系的一般定义:
对任意两个事件A与B , 如果 P(AB)=P(A)P(B)成立,则称事件A与事件B相互独立(mutually independent), 简称为独立.
P(AB)=P(A)P(B) 事件A与B相互独立.
由两个事件相互独立的定义,容易验证必然事件Ω,不可能事件Φ都与任意事件相互独立.
这是因为必然事件Ω总会发生,不会受任何事件是否发生的影响;同样,不可能事件Φ总不会发生,也不受任何事件是否发生的影响. 当然,它们也不影响其他事件是否发生.
一、两个事件相互独立
互为对立的两个事件是非常特殊的一种事件关系. 如果事件A与事件B相互独立,那么它们的对立事件是否也相互独立?
以有放回摸球试验为例,分别验证A与B、A与B、A与B是否独立,你有什么发现?
对于A与因为A=AB∪AB,而且AB与AB互斥,
所以P(A) =P(AB ∪AB)=P(AB)+P(AB)
=P(A)P(B)+P(AB), 所以
P(AB) =P(A)-P(A)P(B)=P(A)(1-P(B))=P(A)P(B)
由事件的独立性定义,A与B相互独立.
类似地,可以证明事件A与B,A与B也都相互独立.
探究2
例1. 一个袋子中有标号分别为1, 2, 3, 4的4个球,除标号外没有其他差异. 采用不放回方式从中任意摸球两次. 设事件A = “第一次摸出球的标号小于3”,事件B =“第二次摸出球的标号小于3”,那么事件A与事件B是否相互独立?
解:∵样本空间为Ω ={(m, n) | m, n∈{1, 2, 3, 4} 且
m ≠ n}, 包含 12 个等可能的样本点. 而 A ={(1, 2), (1, 3),(1, 4), (2, 1),(2, 3), (2, 4)}含 6 个样本点,
B={(m, n) | m∈{1, 2, 3, 4}, n∈{1, 2}且m ≠ n} 含 6 个样本点, ∴AB={(1, 2), (2, 1) }含 2 个样本点.
所以P(A)=P(B)= = , P(AB)= ≠ ×
此时P(AB) ≠ P(A)P(B), 因此, 事件A与事件B不独立.
[题型一] 事件独立性的判断
[题型一] 事件独立性的判断
例3. 甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8 , 乙的中靶概率为0.9 , 求下列事件的概率:
(1) 两人都中靶; (2) 恰好有一人中靶;
(3) 两人都脱靶; (4) 至少有一人中靶.
[题型二] 求相互独立事件的概率
分析:设A=“甲中靶”, B= “乙中靶”, 从要求的概率可知,需要先分别求A,B的对立事件A,B的概率,并利用A, B, A, B构建相应的事件.
例3. 甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8 , 乙的中靶概率为0.9 , 求下列事件的概率:
(1) 两人都中靶; (2) 恰好有一人中靶;
(3) 两人都脱靶; (4) 至少有一人中靶.
[题型二] 求相互独立事件的概率
解:设A=“甲中靶”, B= “乙中靶”, A=“甲脱靶”, B= “乙脱靶”, 由于 甲、乙射击互不影响,∴A与B相互独立,∴A与B ,A与B,A与B也相互独立,
由已知得P(A)=0.8,P(B)=0.9,P(A)=0.2,P(B)=0.1.
(1) AB = “两人都中靶”,由事件独立性的定义,得
P(AB) =P(A)P(B) =0.8×0.9=0.72.
例3. 甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8 , 乙的中靶概率为0.9 , 求下列事件的概率:
(1) 两人都中靶; (2) 恰好有一人中靶;
(3) 两人都脱靶; (4) 至少有一人中靶.
[题型二] 求相互独立事件的概率
解:设A=“甲中靶”, B= “乙中靶”, A=“甲脱靶”, B= “乙脱靶”, 由于 甲、乙射击互不影响,∴A与B相互独立,∴A与B ,A与B,A与B也相互独立,
由已知得P(A)=0.8,P(B)=0.9,P(A)=0.2,P(B)=0.1.
(2)“恰好有一人中靶” =AB∪AB, 且AB与AB互斥,根据概率的加法公式和事件独立性定义,得
P(AB∪AB) =P(AB)+P(AB) =P(A)P(B)+P(A)P(B)
=0.8×0.1+0.2×0.9=0.26.
例3. 甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8 , 乙的中靶概率为0.9 , 求下列事件的概率:
(1) 两人都中靶; (2) 恰好有一人中靶;
(3) 两人都脱靶; (4) 至少有一人中靶.
[题型二] 求相互独立事件的概率
解:设A=“甲中靶”, B= “乙中靶”, A=“甲脱靶”, B= “乙脱靶”, 由于 甲、乙射击互不影响,∴A与B相互独立,∴A与B ,A与B,A与B也相互独立,
由已知得P(A)=0.8,P(B)=0.9,P(A)=0.2,P(B)=0.1.
(3)事件“两人都脱靶” =AB,所以
P(AB) =P(A)P(B)=(1-0.8) × (1-0.9) =0.02.
例3. 甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8 , 乙的中靶概率为0.9 , 求下列事件的概率:
(1) 两人都中靶; (2) 恰好有一人中靶;
(3) 两人都脱靶; (4) 至少有一人中靶.
[题型二] 求相互独立事件的概率
解:设A=“甲中靶”, B= “乙中靶”, A=“甲脱靶”, B= “乙脱靶”, 由于 甲、乙射击互不影响,∴A与B相互独立,∴A与B ,A与B,A与B也相互独立,
由已知得P(A)=0.8,P(B)=0.9,P(A)=0.2,P(B)=0.1.
(4)方法1:由于事件“至少有一人中靶”的对立事件是“两人都脱靶",根据对立事件的性质得,事件“至少有一人中靶”的概率为
1-P(AB) =1-0.02 =0. 98.
例3. 甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8 , 乙的中靶概率为0.9 , 求下列事件的概率:
(1) 两人都中靶; (2) 恰好有一人中靶;
(3) 两人都脱靶; (4) 至少有一人中靶.
[题型二] 求相互独立事件的概率
解:设A=“甲中靶”, B= “乙中靶”, A=“甲脱靶”, B= “乙脱靶”, 由于 甲、乙射击互不影响,∴A与B相互独立,∴A与B ,A与B,A与B也相互独立,
由已知得P(A)=0.8,P(B)=0.9,P(A)=0.2,P(B)=0.1.
(4)方法2:由于事件“至少有一人中靶”=AB∪AB
∪AB,且AB,AB,AB两两互斥,∴事件“至少有一人中靶”的概率为 P(AB∪AB∪AB )=P(AB)+P(AB)+P(AB)=P(A)P(B)+P(A)P(B)+P(A)P(B)
=0. 98.
[题型二] 求相互独立事件的概率
[题型三] 相互独立事件概率的实际应用
例4. 甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语, 已知甲每轮猜对的概率为 ,乙每轮猜对的概率为 . 在每轮活动中,甲和乙猜对与否互不影响,各轮结果也互不影响. 求“星队”在两轮活动中猜对3个成语的概率.
分析:两轮活动猜对3个成语,相当于事件“甲猜对1个,乙猜对2个”、事件“甲猜对2个, 乙猜对1个”的和事件发生.
解:设A1 , A2分别表示甲两轮猜对1个,2个成语的事件,B1 , B2分别表示乙两轮猜对1个,2个成语的事件.根据独立性假定,得
P(A1)=2× × = ; P(A2)=( )2= ,
P(B1)=2× × = ; P(B2)=( )2= .
设A=“两轮活动'星队'猜对3个成语”,则
A=A1B2 ∪A2B1,且A1B2与A2B1互斥,
所以 P(A) = P(A1B2)+P(A2B1) ;
[题型三] 相互独立事件概率的实际应用
课本P.252例3
例4. 甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语, 已知甲每轮猜对的概率为 ,乙每轮猜对的概率为 . 在每轮活动中,甲和乙猜对与否互不影响,各轮结果也互不影响. 求“星队”在两轮活动中猜对3个成语的概率.
[题型三] 相互独立事件概率的实际应用
例4. 甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语, 已知甲每轮猜对的概率为 ,乙每轮猜对的概率为 . 在每轮活动中,甲和乙猜对与否互不影响,各轮结果也互不影响. 求“星队”在两轮活动中猜对3个成语的概率.
解:设A1 , A2分别表示甲两轮猜对1个,2个成语的事件,B1,B2分别表示乙两轮猜对1个,2个成语的事件
所以 P(A) = P(A1B2)+P(A2B1) ;
又∵A1与B2,A2与B1分别相互独立,
∴ P(A) = P(A1)P(B2)+P(A2)P(B1)
= × + × =
因此,“星队”在两轮活动中猜对3个成语的概率是
(2020·全国Ⅰ卷)甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:
累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
解:根据赛制,至少需要进行四场比赛,
至多需要进行五场比赛.
比赛四场结束,共有三种情况:
所以需要进行第五场比赛的概率为
(3)求丙最终获胜的概率.
解:丙最终获胜,有两种情况:
课堂小结
事件A与B相互独立 P(AB)=P(A)P(B)
3. 求相互独立事件的概率
10.2 事件的相互独立性
学习目标
1.了解两个随机事件相互独立的含义;
2.结合古典概型,利用独立性计算概率;
3.能利用相互独立性事件同时发生的概率公式解决一些简单的实际问题.
核心素养
数学抽象、数学建模、逻辑推理。
温故知新
温故知新
新课导入
前面我们研究过互斥事件、对立事件的概率性质,还研究过和事件的概率计算方法.
对于积事件的概率,你能提出什么值得研究的问题吗? 我们知道,积事件AB就是事件A与事件B同时发生. 因此,积事件AB发生的概率一定与事件A,B发生的概率有关. 那么,这种关系会是怎样的呢?
下面我们来讨论一类与积事件有关的特殊问题.
探究1
下面两个随机试验各定义了一对随机事件A和B,你觉得事件A发生与否会影响事件B发生的概率吗?
试验1:分别抛掷两枚质地均匀的硬币,A= “第一枚硬币正面朝上”,B=“第二枚硬币反面朝上”.
试验2: —个袋子中装有标号分别是1, 2, 3, 4的4个球,除标号外没有其它差异. 采用有放回方式从袋中依次任意摸出两球. A= “第一次摸到球的标号小于3”,B = “第二次摸到球的标号小于3”.
分别计算P(A),P(B),P(AB),你有什么发现?
新课讲解
因为两枚硬币分别拋掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率.
下面两个随机试验各定义了一对随机事件A和B,你觉得事件A发生与否会影响事件B发生的概率吗?
试验1:分别抛掷两枚质地均匀的硬币,A= “第一枚硬币正面朝上”,B=“第二枚硬币反面朝上”.
计算P(A),P(B),P(AB),你有什么发现?
新课讲解
下面两个随机试验各定义了一对随机事件A和B,你觉得事件A发生与否会影响事件B发生的概率吗?
试验1:分别抛掷两枚质地均匀的硬币,A= “第一枚硬币正面朝上”,B=“第二枚硬币反面朝上”.
计算P(A),P(B),P(AB),你有什么发现?
用1表示硬币“正面朝上”,用0表示硬币“反面朝上”,则样本空间为Ω ={(1, 1), (1, 0), (0, 1), (0, 0)}, 包含 4 个等可能的样本点. 而 A ={(1, 1), (1, 0)}, B={(1, 0), (0, 0)}, 所以AB={(1, 0)}. 由古典概型概率计算公式,得
P(A)=P(B)= , P(AB)= . 于是P(AB)=P(A)P(B).
积事件AB的概率P(AB)恰好等于P(A)与P(B)的乘积.
试验2 一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异,采用有放回方式从袋中依次任意摸出两球.设A=“第一次摸到球的标号小于3”, B=“第二次摸到球的标号小于3”.
第一次 第二次 1 2 3 4
1 (1,1) (1,2) (1,3) (1,4)
2 (2,1) (2,2) (2,3) (2,4)
3 (3,1) (3,2) (3,3) (3,4)
4 (4,1) (4,2) (4,3) (4,4)
第一次 第二次 1 2 3 4
1 (1,1) (1,2) (1,3) (1,4)
2 (2,1) (2,2) (2,3) (2,4)
3 (3,1) (3,2) (3,3) (3,4)
4 (4,1) (4,2) (4,3) (4,4)
试验2 一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异,采用有放回方式从袋中依次任意摸出两球.设A=“第一次摸到球的标号小于3”, B=“第二次摸到球的标号小于3”.
即 积事件AB的概率P(AB)恰好等于P(A)与P(B)的乘积.
从上述两个试验的共性中得到启发,我们引入这种事件关系的一般定义:
对任意两个事件A与B , 如果 P(AB)=P(A)P(B)成立,则称事件A与事件B相互独立(mutually independent), 简称为独立.
P(AB)=P(A)P(B) 事件A与B相互独立.
由两个事件相互独立的定义,容易验证必然事件Ω,不可能事件Φ都与任意事件相互独立.
这是因为必然事件Ω总会发生,不会受任何事件是否发生的影响;同样,不可能事件Φ总不会发生,也不受任何事件是否发生的影响. 当然,它们也不影响其他事件是否发生.
一、两个事件相互独立
互为对立的两个事件是非常特殊的一种事件关系. 如果事件A与事件B相互独立,那么它们的对立事件是否也相互独立?
以有放回摸球试验为例,分别验证A与B、A与B、A与B是否独立,你有什么发现?
对于A与因为A=AB∪AB,而且AB与AB互斥,
所以P(A) =P(AB ∪AB)=P(AB)+P(AB)
=P(A)P(B)+P(AB), 所以
P(AB) =P(A)-P(A)P(B)=P(A)(1-P(B))=P(A)P(B)
由事件的独立性定义,A与B相互独立.
类似地,可以证明事件A与B,A与B也都相互独立.
探究2
例1. 一个袋子中有标号分别为1, 2, 3, 4的4个球,除标号外没有其他差异. 采用不放回方式从中任意摸球两次. 设事件A = “第一次摸出球的标号小于3”,事件B =“第二次摸出球的标号小于3”,那么事件A与事件B是否相互独立?
解:∵样本空间为Ω ={(m, n) | m, n∈{1, 2, 3, 4} 且
m ≠ n}, 包含 12 个等可能的样本点. 而 A ={(1, 2), (1, 3),(1, 4), (2, 1),(2, 3), (2, 4)}含 6 个样本点,
B={(m, n) | m∈{1, 2, 3, 4}, n∈{1, 2}且m ≠ n} 含 6 个样本点, ∴AB={(1, 2), (2, 1) }含 2 个样本点.
所以P(A)=P(B)= = , P(AB)= ≠ ×
此时P(AB) ≠ P(A)P(B), 因此, 事件A与事件B不独立.
[题型一] 事件独立性的判断
[题型一] 事件独立性的判断
例3. 甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8 , 乙的中靶概率为0.9 , 求下列事件的概率:
(1) 两人都中靶; (2) 恰好有一人中靶;
(3) 两人都脱靶; (4) 至少有一人中靶.
[题型二] 求相互独立事件的概率
分析:设A=“甲中靶”, B= “乙中靶”, 从要求的概率可知,需要先分别求A,B的对立事件A,B的概率,并利用A, B, A, B构建相应的事件.
例3. 甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8 , 乙的中靶概率为0.9 , 求下列事件的概率:
(1) 两人都中靶; (2) 恰好有一人中靶;
(3) 两人都脱靶; (4) 至少有一人中靶.
[题型二] 求相互独立事件的概率
解:设A=“甲中靶”, B= “乙中靶”, A=“甲脱靶”, B= “乙脱靶”, 由于 甲、乙射击互不影响,∴A与B相互独立,∴A与B ,A与B,A与B也相互独立,
由已知得P(A)=0.8,P(B)=0.9,P(A)=0.2,P(B)=0.1.
(1) AB = “两人都中靶”,由事件独立性的定义,得
P(AB) =P(A)P(B) =0.8×0.9=0.72.
例3. 甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8 , 乙的中靶概率为0.9 , 求下列事件的概率:
(1) 两人都中靶; (2) 恰好有一人中靶;
(3) 两人都脱靶; (4) 至少有一人中靶.
[题型二] 求相互独立事件的概率
解:设A=“甲中靶”, B= “乙中靶”, A=“甲脱靶”, B= “乙脱靶”, 由于 甲、乙射击互不影响,∴A与B相互独立,∴A与B ,A与B,A与B也相互独立,
由已知得P(A)=0.8,P(B)=0.9,P(A)=0.2,P(B)=0.1.
(2)“恰好有一人中靶” =AB∪AB, 且AB与AB互斥,根据概率的加法公式和事件独立性定义,得
P(AB∪AB) =P(AB)+P(AB) =P(A)P(B)+P(A)P(B)
=0.8×0.1+0.2×0.9=0.26.
例3. 甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8 , 乙的中靶概率为0.9 , 求下列事件的概率:
(1) 两人都中靶; (2) 恰好有一人中靶;
(3) 两人都脱靶; (4) 至少有一人中靶.
[题型二] 求相互独立事件的概率
解:设A=“甲中靶”, B= “乙中靶”, A=“甲脱靶”, B= “乙脱靶”, 由于 甲、乙射击互不影响,∴A与B相互独立,∴A与B ,A与B,A与B也相互独立,
由已知得P(A)=0.8,P(B)=0.9,P(A)=0.2,P(B)=0.1.
(3)事件“两人都脱靶” =AB,所以
P(AB) =P(A)P(B)=(1-0.8) × (1-0.9) =0.02.
例3. 甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8 , 乙的中靶概率为0.9 , 求下列事件的概率:
(1) 两人都中靶; (2) 恰好有一人中靶;
(3) 两人都脱靶; (4) 至少有一人中靶.
[题型二] 求相互独立事件的概率
解:设A=“甲中靶”, B= “乙中靶”, A=“甲脱靶”, B= “乙脱靶”, 由于 甲、乙射击互不影响,∴A与B相互独立,∴A与B ,A与B,A与B也相互独立,
由已知得P(A)=0.8,P(B)=0.9,P(A)=0.2,P(B)=0.1.
(4)方法1:由于事件“至少有一人中靶”的对立事件是“两人都脱靶",根据对立事件的性质得,事件“至少有一人中靶”的概率为
1-P(AB) =1-0.02 =0. 98.
例3. 甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8 , 乙的中靶概率为0.9 , 求下列事件的概率:
(1) 两人都中靶; (2) 恰好有一人中靶;
(3) 两人都脱靶; (4) 至少有一人中靶.
[题型二] 求相互独立事件的概率
解:设A=“甲中靶”, B= “乙中靶”, A=“甲脱靶”, B= “乙脱靶”, 由于 甲、乙射击互不影响,∴A与B相互独立,∴A与B ,A与B,A与B也相互独立,
由已知得P(A)=0.8,P(B)=0.9,P(A)=0.2,P(B)=0.1.
(4)方法2:由于事件“至少有一人中靶”=AB∪AB
∪AB,且AB,AB,AB两两互斥,∴事件“至少有一人中靶”的概率为 P(AB∪AB∪AB )=P(AB)+P(AB)+P(AB)=P(A)P(B)+P(A)P(B)+P(A)P(B)
=0. 98.
[题型二] 求相互独立事件的概率
[题型三] 相互独立事件概率的实际应用
例4. 甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语, 已知甲每轮猜对的概率为 ,乙每轮猜对的概率为 . 在每轮活动中,甲和乙猜对与否互不影响,各轮结果也互不影响. 求“星队”在两轮活动中猜对3个成语的概率.
分析:两轮活动猜对3个成语,相当于事件“甲猜对1个,乙猜对2个”、事件“甲猜对2个, 乙猜对1个”的和事件发生.
解:设A1 , A2分别表示甲两轮猜对1个,2个成语的事件,B1 , B2分别表示乙两轮猜对1个,2个成语的事件.根据独立性假定,得
P(A1)=2× × = ; P(A2)=( )2= ,
P(B1)=2× × = ; P(B2)=( )2= .
设A=“两轮活动'星队'猜对3个成语”,则
A=A1B2 ∪A2B1,且A1B2与A2B1互斥,
所以 P(A) = P(A1B2)+P(A2B1) ;
[题型三] 相互独立事件概率的实际应用
课本P.252例3
例4. 甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语, 已知甲每轮猜对的概率为 ,乙每轮猜对的概率为 . 在每轮活动中,甲和乙猜对与否互不影响,各轮结果也互不影响. 求“星队”在两轮活动中猜对3个成语的概率.
[题型三] 相互独立事件概率的实际应用
例4. 甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语, 已知甲每轮猜对的概率为 ,乙每轮猜对的概率为 . 在每轮活动中,甲和乙猜对与否互不影响,各轮结果也互不影响. 求“星队”在两轮活动中猜对3个成语的概率.
解:设A1 , A2分别表示甲两轮猜对1个,2个成语的事件,B1,B2分别表示乙两轮猜对1个,2个成语的事件
所以 P(A) = P(A1B2)+P(A2B1) ;
又∵A1与B2,A2与B1分别相互独立,
∴ P(A) = P(A1)P(B2)+P(A2)P(B1)
= × + × =
因此,“星队”在两轮活动中猜对3个成语的概率是
(2020·全国Ⅰ卷)甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:
累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
解:根据赛制,至少需要进行四场比赛,
至多需要进行五场比赛.
比赛四场结束,共有三种情况:
所以需要进行第五场比赛的概率为
(3)求丙最终获胜的概率.
解:丙最终获胜,有两种情况:
课堂小结
事件A与B相互独立 P(AB)=P(A)P(B)
3. 求相互独立事件的概率
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
