人教A版(2019)选择性必修一 2.2.2 两点式方程 课件(19张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修一 2.2.2 两点式方程 课件(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 337.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-19 23:39:41 | ||
图片预览




文档简介
(共19张PPT)
2.2.2直线的两点式方程
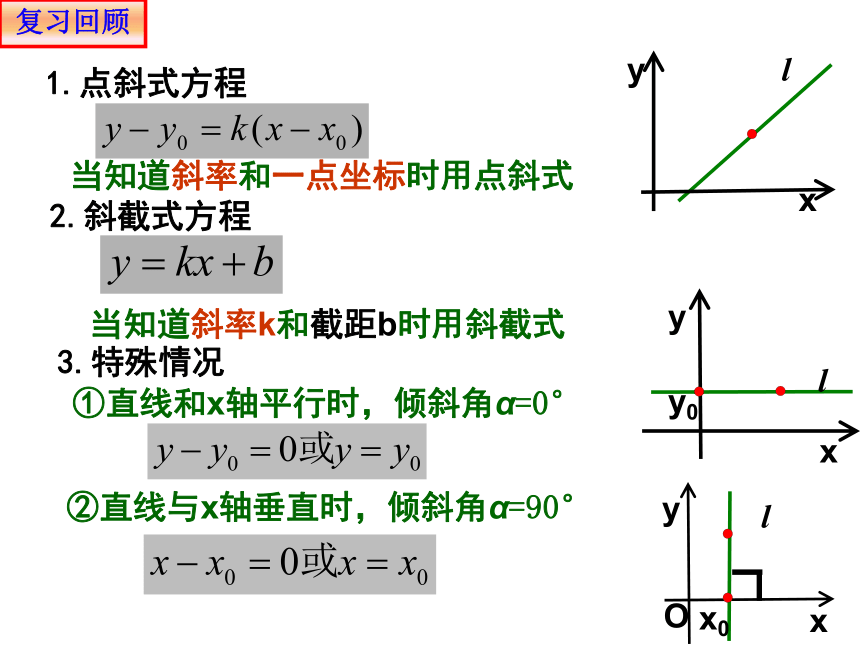
1.点斜式方程
当知道斜率和一点坐标时用点斜式
2.斜截式方程
当知道斜率k和截距b时用斜截式
3.特殊情况
①直线和x轴平行时,倾斜角α=0°
②直线与x轴垂直时,倾斜角α=90°
x
y
l
x
y
l
y0
l
x
y
O
x0
复习回顾
我们知道在直角坐标系内确定一条直线的几何要素:
(1)点和倾斜角(斜率),即已知直线上的一点和直线的斜率可以确定一条直线.
(2)点和方向,即已知直线上的一点和直线的方向向量可以确定一条直线(P68)
(3)已知两点也可以确定一条直线.
这样,在直角坐标系中,给定一个点p0(x0,y0)和斜率k,可得出直线方程。
若给定直线上两点p1(x1,y1)p2(x2,y2),你能否得出直线的方程呢
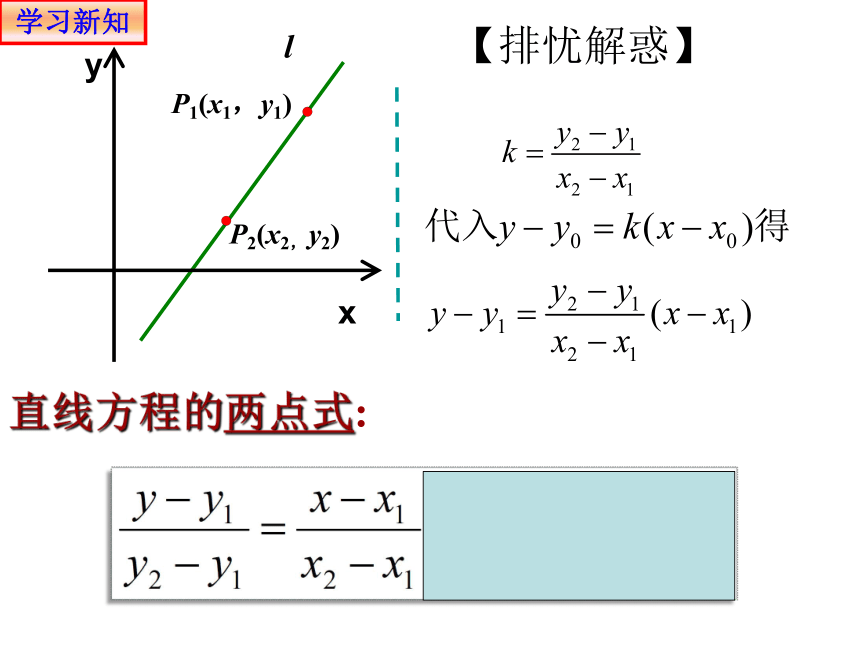
已知直线上两点P1(x1,y1), P2(x2,y2),如何求出通过这两点的直线方程呢?
请同桌同学共同努力,用你认为比较和谐的形式表示直线方程。
思考:
学习新知
尝试:
x
y
l
P2(x2,y2)
P1(x1,y1)
【排忧解惑】
直线方程的两点式:
学习新知
讨论:两点式方程不适用于什么直线?
当直线没有斜率或斜率为0时,即平行于坐标轴或与坐标轴重合的直线不能用两点式求出它们的方程。
直线方程的两点式:
若点P1 ( x1 , y1 ),P2( x2 , y2)中有x1 =x2或y1= y2,此时过这两点的直线方程是什么?
当x1 =x2 时方程为: x =x1
当 y1= y2时方程为: y= y1
学习新知
x
y
A(-5,0)
C(0,2)
B(3,-3)
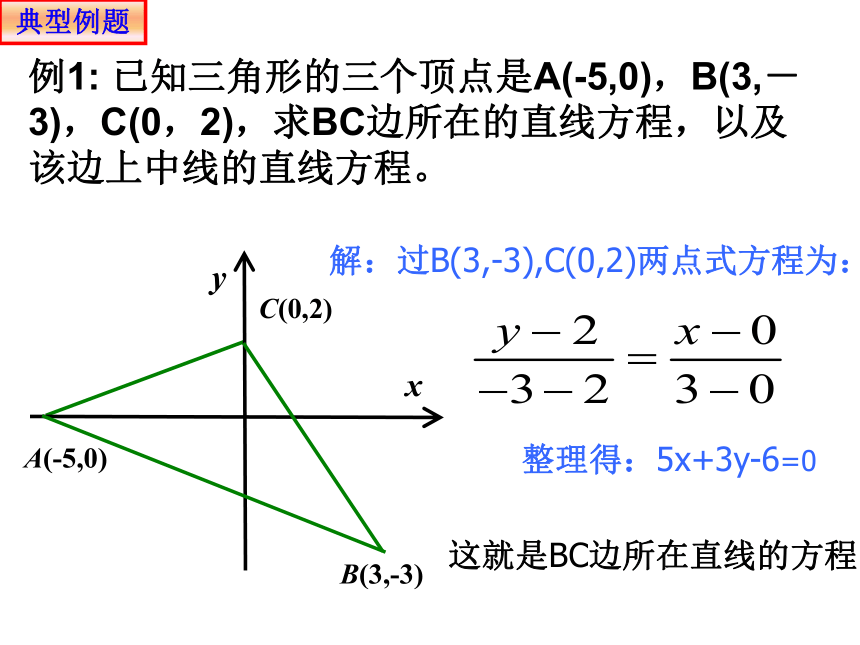
例1: 已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在的直线方程,以及该边上中线的直线方程。
解:过B(3,-3),C(0,2)两点式方程为:
整理得:5x+3y-6=0
这就是BC边所在直线的方程。
典型例题
x
y
A(-5,0)
M(xM,yM)
中点
C(0,2)
B(3,-3)
x+13y+5=0
典型例题
例1: 已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在的直线方程,以及该边上中线的直线方程。
解:将两点A(a,0), B(0,b)的坐标代入两点式,得:
即:
所以直线l的方程为:
例2、已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求这条直线l的方程.
x
l
B
A
O
y
学习新知
x
l
A(a,0)
B(0,b)
a为直线在x轴上的截距
b为直线在y轴上的截距
截距式方程:
学习新知
y
O
不能表示过原点或与坐标轴平行或重合的直线
讨论:
是不是任意一条直线都有截距式方程呢?
截距式方程:
学习新知
(2)若直线l在两坐标轴上的截距相等,
则直线l的方程:
注:(1)截距式适用于与两坐标轴不垂直
且不过原点的直线。
x+y=a
或y=kx
(3)若直线l在两坐标轴上的截距互为相反数,
则直线l的方程:
x-y=a
或y=kx
(4)若直线l在两坐标轴上的截距绝对值相等,
则直线l的方程:
x+y=a
或y=kx
或x-y=a
B
巩固练习
1.求过(1,2)并且在两个坐标轴上的截距相等的直线的斜截式方程。
1.解:
y=2x (与x轴和y轴的截距都为0)
所以直线方程为:y=-x+3
即:a=3
把(1,2)代入得:
设 直线的方程为:
巩固练习
2.过(1,2)并且在两个坐标轴上的截距的绝对值相等的直线的斜截式方程。
解:三条
⑵ 过(1,2)并且在两个坐标轴上的截距的绝对值相等的直线的斜截式方程。
解得:a=b=3或a=-b=-1
直线方程为:y=-x+3=0、y=x+1或y=2x
设
练习课本第64页练习2,3
巩固练习
过点P(1,3),且与x轴、y轴的正半轴围成的三角形的面积等于6的直线方程是( )
A.3x+y-6=0 B.x+3y-10=0 C.3x-y=0 D.x-3y+8=0
巩固练习
总结归纳:在涉及直线与两个坐标轴的截距问题时,常把直线方程设为截距式,由已知条件建立关于两截距的方程,解得截距的值,从而确定方程.
追问:求当围成的三角形面积最小时,直线的方程。
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
知识小结
已知△ABC三顶点A(1,2),B(3,6),C(5,2),M为AB的中点,N为AC的中点,则中位线MN所在的直线方程为( )
A.2x+y-8=0 B.2x-y+8=0 C.2x+y-12=0 D.2x-y-12=0
巩固练习
A
直线ax+by=1(ab≠0)与两坐标轴围成的三角形的面积是 .
如图,某小区内有一块荒地ABCDE,已知BC=210 m,CD=240 m,DE=300 m,EA=180 m,AE∥CD,BC∥DE,∠C=90°,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发.问如何设计才能使开发的面积最大 最大开发面积是多少
应用数学
解:以BC所在直线为x轴,AE所在直线为y轴建立平面直角坐标系(如图),由已知可得A(0,60),B(90,0),
2.2.2直线的两点式方程
1.点斜式方程
当知道斜率和一点坐标时用点斜式
2.斜截式方程
当知道斜率k和截距b时用斜截式
3.特殊情况
①直线和x轴平行时,倾斜角α=0°
②直线与x轴垂直时,倾斜角α=90°
x
y
l
x
y
l
y0
l
x
y
O
x0
复习回顾
我们知道在直角坐标系内确定一条直线的几何要素:
(1)点和倾斜角(斜率),即已知直线上的一点和直线的斜率可以确定一条直线.
(2)点和方向,即已知直线上的一点和直线的方向向量可以确定一条直线(P68)
(3)已知两点也可以确定一条直线.
这样,在直角坐标系中,给定一个点p0(x0,y0)和斜率k,可得出直线方程。
若给定直线上两点p1(x1,y1)p2(x2,y2),你能否得出直线的方程呢
已知直线上两点P1(x1,y1), P2(x2,y2),如何求出通过这两点的直线方程呢?
请同桌同学共同努力,用你认为比较和谐的形式表示直线方程。
思考:
学习新知
尝试:
x
y
l
P2(x2,y2)
P1(x1,y1)
【排忧解惑】
直线方程的两点式:
学习新知
讨论:两点式方程不适用于什么直线?
当直线没有斜率或斜率为0时,即平行于坐标轴或与坐标轴重合的直线不能用两点式求出它们的方程。
直线方程的两点式:
若点P1 ( x1 , y1 ),P2( x2 , y2)中有x1 =x2或y1= y2,此时过这两点的直线方程是什么?
当x1 =x2 时方程为: x =x1
当 y1= y2时方程为: y= y1
学习新知
x
y
A(-5,0)
C(0,2)
B(3,-3)
例1: 已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在的直线方程,以及该边上中线的直线方程。
解:过B(3,-3),C(0,2)两点式方程为:
整理得:5x+3y-6=0
这就是BC边所在直线的方程。
典型例题
x
y
A(-5,0)
M(xM,yM)
中点
C(0,2)
B(3,-3)
x+13y+5=0
典型例题
例1: 已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在的直线方程,以及该边上中线的直线方程。
解:将两点A(a,0), B(0,b)的坐标代入两点式,得:
即:
所以直线l的方程为:
例2、已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求这条直线l的方程.
x
l
B
A
O
y
学习新知
x
l
A(a,0)
B(0,b)
a为直线在x轴上的截距
b为直线在y轴上的截距
截距式方程:
学习新知
y
O
不能表示过原点或与坐标轴平行或重合的直线
讨论:
是不是任意一条直线都有截距式方程呢?
截距式方程:
学习新知
(2)若直线l在两坐标轴上的截距相等,
则直线l的方程:
注:(1)截距式适用于与两坐标轴不垂直
且不过原点的直线。
x+y=a
或y=kx
(3)若直线l在两坐标轴上的截距互为相反数,
则直线l的方程:
x-y=a
或y=kx
(4)若直线l在两坐标轴上的截距绝对值相等,
则直线l的方程:
x+y=a
或y=kx
或x-y=a
B
巩固练习
1.求过(1,2)并且在两个坐标轴上的截距相等的直线的斜截式方程。
1.解:
y=2x (与x轴和y轴的截距都为0)
所以直线方程为:y=-x+3
即:a=3
把(1,2)代入得:
设 直线的方程为:
巩固练习
2.过(1,2)并且在两个坐标轴上的截距的绝对值相等的直线的斜截式方程。
解:三条
⑵ 过(1,2)并且在两个坐标轴上的截距的绝对值相等的直线的斜截式方程。
解得:a=b=3或a=-b=-1
直线方程为:y=-x+3=0、y=x+1或y=2x
设
练习课本第64页练习2,3
巩固练习
过点P(1,3),且与x轴、y轴的正半轴围成的三角形的面积等于6的直线方程是( )
A.3x+y-6=0 B.x+3y-10=0 C.3x-y=0 D.x-3y+8=0
巩固练习
总结归纳:在涉及直线与两个坐标轴的截距问题时,常把直线方程设为截距式,由已知条件建立关于两截距的方程,解得截距的值,从而确定方程.
追问:求当围成的三角形面积最小时,直线的方程。
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
知识小结
已知△ABC三顶点A(1,2),B(3,6),C(5,2),M为AB的中点,N为AC的中点,则中位线MN所在的直线方程为( )
A.2x+y-8=0 B.2x-y+8=0 C.2x+y-12=0 D.2x-y-12=0
巩固练习
A
直线ax+by=1(ab≠0)与两坐标轴围成的三角形的面积是 .
如图,某小区内有一块荒地ABCDE,已知BC=210 m,CD=240 m,DE=300 m,EA=180 m,AE∥CD,BC∥DE,∠C=90°,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发.问如何设计才能使开发的面积最大 最大开发面积是多少
应用数学
解:以BC所在直线为x轴,AE所在直线为y轴建立平面直角坐标系(如图),由已知可得A(0,60),B(90,0),
