人教A版(2019)选择性必修一 2.2.3 直线的一般式方程 课件(15张ppt)
文档属性
| 名称 | 人教A版(2019)选择性必修一 2.2.3 直线的一般式方程 课件(15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 371.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-19 23:40:13 | ||
图片预览






文档简介
(共15张PPT)
2.2.3直线的一般式方程
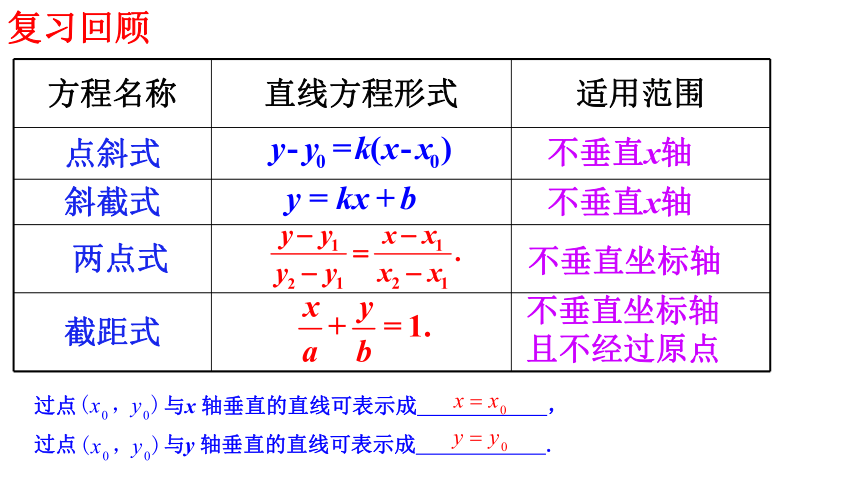
方程名称 直线方程形式 适用范围
点斜式
斜截式
两点式
截距式
不垂直x轴
不垂直x轴
不垂直坐标轴
不垂直坐标轴且不经过原点
复习回顾
过点 与x 轴垂直的直线可表示成 ,
过点 与y 轴垂直的直线可表示成 .
上述四种直线方程,能否写成如下统一形式?Ax + B y + C =0
以上情况都可以写成直线方程的一般形式:Ax+By+C=0, A、B不同时为0。
结论:平面上任意一条直线都可以用一个关于 x , y 的二元一次方程表示.
Ax+By+C=0 (A、B不同时为0)
由上可知:关于x,y的二元一次方程都表示一条直线.
对于问题(2),如果能把任意一个二元一次方程 (A,B不同时为0)化为直线的某种形式,那么它就表示一条直线.
当 时,方程可变形为 ,它表示过点 ,斜率为 的直线;
当 , 时,方程可变形为 ,它表示过点 ,垂直于x 轴的一条直线
思考 (2)任意一个关于x,y 的二元一次方程都表示一条直线吗?
O
y
3
x
1
2
1
2
3
4
A
B
结合例1,我们可以从几何角度看一个二元一次方程,
即一个二元一次方程表示一条直线.
练: 判断下列各对直线是平行还是垂直,并说明理由.
(1) , ;
(2) , .
2.两直线位置关系的判断
直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,
试讨论: (1) l1∥l2 (2) l1⊥l2
A2≠0,B2≠0,C2≠0,
先观察斜率是否存在,
再看斜率是否相等,
l1⊥l2
A1A2+B1B2=0
例3
(1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求实数m的值;
(2)已知直线l1:(a+2)x+(1-a)y-1=0与直线l2:(a-1)x+(2a+3)y+2=0垂直,求实数a的值.
(1)由2×3-m(m+1)=0,得m=-3或m=2.当m=-3时,l1:x-y+2=0,l2:3x-3y+2=0,显然l1与l2不重合,∴l1∥l2.
同理,当m=2时,l1:2x+3y+4=0,l2:2x+3y-2=0,l1与l2不重合,l1∥l2,故m的值为2或-3.
(2)由直线l1⊥l2,得(a+2)(a-1)+(1-a)(2a+3)=0,解得a=±1.
故当a=1或a=-1时,直线l1⊥l2.
3.直线系方程
1)与直线l:Ax+By+C=0 平行的直线系方程为:Ax+By+m=0
(其中m≠C,m为待定系数)
O
x
y
Ax+By+C=0
只是常数不一样,其余相同
2)与直线l:Ax+By+C=0 垂直的直线系方程为:Bx-Ay+m=0
(m为待定系数)
O
x
y
Ax+By+C=0
例4 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线方程:
(1)过点(-1,3)且与l平行;(2)过点(-1,3)且与l垂直.
(1)设所求的直线方程为:3x+4y+m=0
把点(-1,3)代入方程,得
m=-9,方程为3x+4y-9=0
(2)设所求的直线方程为:4x-3y+n=0
把点(-1,3)代入方程,得
n=13,方程为4x-3y+13=0
与含参数的一般式方程有关的问题
直线过定点问题
例5 已知方程(m+2)x+(m-3)y+4=0(m∈R)所表示的直线恒过定点,试求该定点的坐标.
方法一:令m=-2,则方程变为-5y+4=0,
令m=3,则方程变为5x+4=0,
方法二:将方程变形为m(x+y)+2x-3y+4=0.
x+y=0
2x-3y+4=0
1.直线
(1)若 .
(2)若 .
2.与直线 平行的直线可设为
与直线 垂直的直线可设为
1.直线方程的一般式Ax+By+C=0(A,B不同时为零)
2.直线方程的一般式与特殊式的互化.
3.两条直线平行与垂直的判定.
注意B=0
两方面含义:
(1)直线方程都是关于x, y的二元一次方程;
(2)关于x, y的二元一次方程的图象又都是一条直线.
2.2.3直线的一般式方程
方程名称 直线方程形式 适用范围
点斜式
斜截式
两点式
截距式
不垂直x轴
不垂直x轴
不垂直坐标轴
不垂直坐标轴且不经过原点
复习回顾
过点 与x 轴垂直的直线可表示成 ,
过点 与y 轴垂直的直线可表示成 .
上述四种直线方程,能否写成如下统一形式?Ax + B y + C =0
以上情况都可以写成直线方程的一般形式:Ax+By+C=0, A、B不同时为0。
结论:平面上任意一条直线都可以用一个关于 x , y 的二元一次方程表示.
Ax+By+C=0 (A、B不同时为0)
由上可知:关于x,y的二元一次方程都表示一条直线.
对于问题(2),如果能把任意一个二元一次方程 (A,B不同时为0)化为直线的某种形式,那么它就表示一条直线.
当 时,方程可变形为 ,它表示过点 ,斜率为 的直线;
当 , 时,方程可变形为 ,它表示过点 ,垂直于x 轴的一条直线
思考 (2)任意一个关于x,y 的二元一次方程都表示一条直线吗?
O
y
3
x
1
2
1
2
3
4
A
B
结合例1,我们可以从几何角度看一个二元一次方程,
即一个二元一次方程表示一条直线.
练: 判断下列各对直线是平行还是垂直,并说明理由.
(1) , ;
(2) , .
2.两直线位置关系的判断
直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,
试讨论: (1) l1∥l2 (2) l1⊥l2
A2≠0,B2≠0,C2≠0,
先观察斜率是否存在,
再看斜率是否相等,
l1⊥l2
A1A2+B1B2=0
例3
(1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求实数m的值;
(2)已知直线l1:(a+2)x+(1-a)y-1=0与直线l2:(a-1)x+(2a+3)y+2=0垂直,求实数a的值.
(1)由2×3-m(m+1)=0,得m=-3或m=2.当m=-3时,l1:x-y+2=0,l2:3x-3y+2=0,显然l1与l2不重合,∴l1∥l2.
同理,当m=2时,l1:2x+3y+4=0,l2:2x+3y-2=0,l1与l2不重合,l1∥l2,故m的值为2或-3.
(2)由直线l1⊥l2,得(a+2)(a-1)+(1-a)(2a+3)=0,解得a=±1.
故当a=1或a=-1时,直线l1⊥l2.
3.直线系方程
1)与直线l:Ax+By+C=0 平行的直线系方程为:Ax+By+m=0
(其中m≠C,m为待定系数)
O
x
y
Ax+By+C=0
只是常数不一样,其余相同
2)与直线l:Ax+By+C=0 垂直的直线系方程为:Bx-Ay+m=0
(m为待定系数)
O
x
y
Ax+By+C=0
例4 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线方程:
(1)过点(-1,3)且与l平行;(2)过点(-1,3)且与l垂直.
(1)设所求的直线方程为:3x+4y+m=0
把点(-1,3)代入方程,得
m=-9,方程为3x+4y-9=0
(2)设所求的直线方程为:4x-3y+n=0
把点(-1,3)代入方程,得
n=13,方程为4x-3y+13=0
与含参数的一般式方程有关的问题
直线过定点问题
例5 已知方程(m+2)x+(m-3)y+4=0(m∈R)所表示的直线恒过定点,试求该定点的坐标.
方法一:令m=-2,则方程变为-5y+4=0,
令m=3,则方程变为5x+4=0,
方法二:将方程变形为m(x+y)+2x-3y+4=0.
x+y=0
2x-3y+4=0
1.直线
(1)若 .
(2)若 .
2.与直线 平行的直线可设为
与直线 垂直的直线可设为
1.直线方程的一般式Ax+By+C=0(A,B不同时为零)
2.直线方程的一般式与特殊式的互化.
3.两条直线平行与垂直的判定.
注意B=0
两方面含义:
(1)直线方程都是关于x, y的二元一次方程;
(2)关于x, y的二元一次方程的图象又都是一条直线.
