鲁教版五四制初二数学第一单元1.3全等三角形对应练习(含答案)
文档属性
| 名称 | 鲁教版五四制初二数学第一单元1.3全等三角形对应练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 137.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-03 00:00:00 | ||
图片预览

文档简介
鲁教版五四制初二数学第一单元1.3全等三角形对应练习
一.选择题(共8小题)
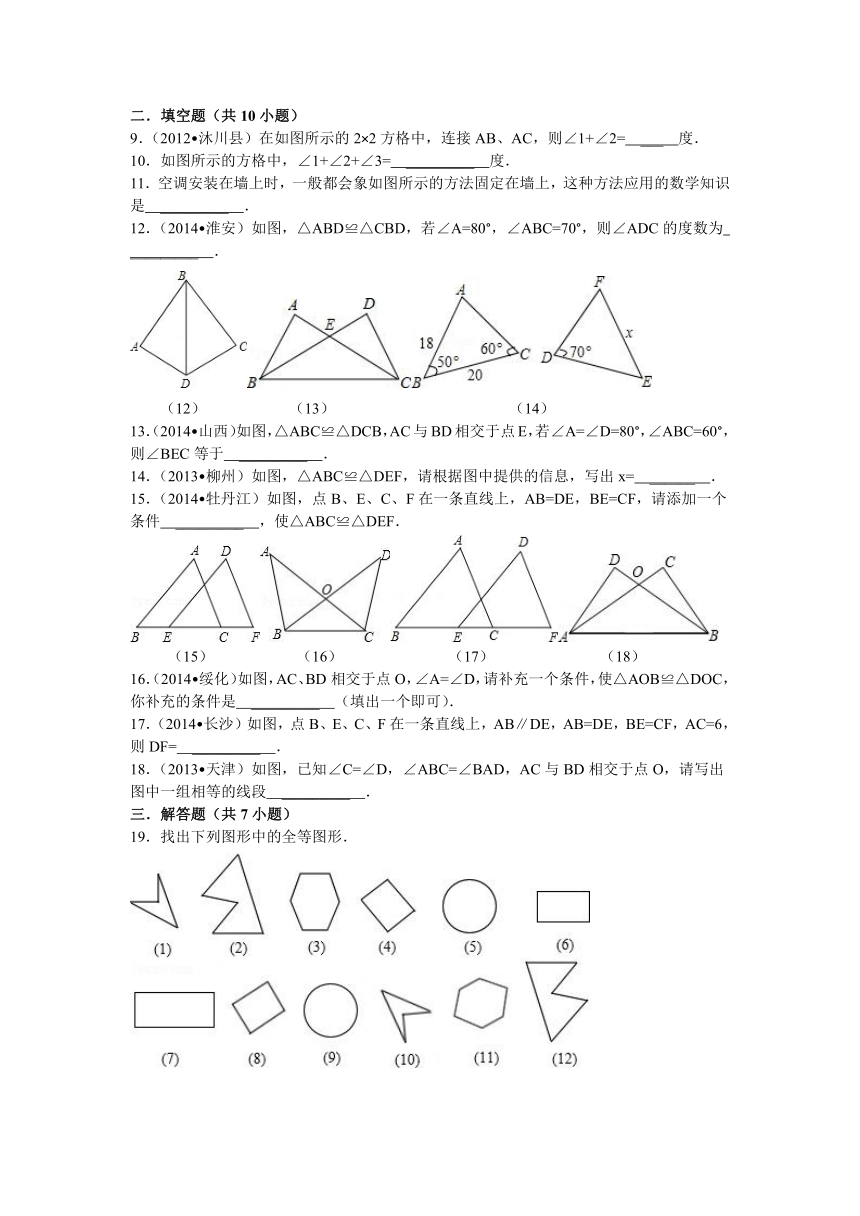
1.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B. 60° C. 58° D. 50°
(1) (3) (4)
2.如果两个图形全等,则这个图形必定是( )
A.形状相同,但大小不同 B. 形状大小均相同
C.大小相同,但形状不同 D. 形状大小均不相同
3.如图,△ABC≌△DEF,则此图中相等的线段有( )
A.1对 B. 2对 C. 3对 D. 4对
4.(2013 金平区)木工师傅在做完门框后,为防止变形常常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的根据是( )
A.矩形的对称性 B. 矩形的四个角都是直角
C.三角形的稳定性 D. 两点之间线段最短
5.(2004 南山区)如图,若△ABC≌△DEF,则∠E等于( )
A.30° B. 50° C. 60° D. 100°
(5) (6) (7)
6.如图,若△ABC≌△ADE,则下列结论不正确的是( )
A.AB=AD B. AC=AD C. AC=AE D. BC=DE
7.(2014 黔西南州)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
8.(2014 塘沽区)如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.∠B=∠C B. ∠BDA=∠CDA C. AB=AC D. BD=CD
(8) (9) (10) (11)
二.填空题(共10小题)
9.(2012 沐川县)在如图所示的2×2方格中,连接AB、AC,则∠1+∠2= ___ 度.
10.如图所示的方格中,∠1+∠2+∠3= _________ 度.
11.空调安装在墙上时,一般都会象如图所示的方法固定在墙上,这种方法应用的数学知识是 _________ .
12.(2014 淮安)如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠ADC的度数为 _________ .
(12) (13) (14)
13.(2014 山西)如图,△ABC≌△DCB,AC与BD相交于点E,若∠A=∠D=80°,∠ABC=60°,则∠BEC等于 _________ .
14.(2013 柳州)如图,△ABC≌△DEF,请根据图中提供的信息,写出x= ______ .
15.(2014 牡丹江)如图,点B、E、C、F在一条直线上,AB=DE,BE=CF,请添加一个条件 _________ ,使△ABC≌△DEF.
(15) (16) (17) (18)
16.(2014 绥化)如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是 _________ (填出一个即可).
17.(2014 长沙)如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF= _________ .
18.(2013 天津)如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,请写出图中一组相等的线段 _________ .
三.解答题(共7小题)
19.找出下列图形中的全等图形.
20.(2014 常州)已知:如图,点C为AB中点,CD=BE,CD∥BE.
求证:△ACD≌△CBE.
21.(2014 漳州)如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)
22.(2014 吉林)如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,
求证:△ABD≌△AEC.
23.(2014 硚口区二模)如图,已知AE=CF,∠AFD=∠CEB,∠A=∠C,求证:△ADF≌△CBE.
24.(2014 昆明)已知:如图,点A、B、C在同一直线上,AB=CD,AE∥CF,且AE=CF.
求证:∠E=∠F.
25.(2014 宜昌)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.
鲁教版五四制初二数学第一单元1.3全等三角形对应练习参考答案
一.选择题(共8小题)
1.D.2.B.3.D.4.C.5.D.6.B.7.C.8.D.
二.填空题(共10小题)
9. 90 10. 135 11.三角形的稳定性 12. 130° 13. 100° 14. 20
15. AC=DF(或∠B=∠DEF或AB∥DE)
16.AB=CD(答案不唯一) 17. 6 18. AC=BD(答案不唯一)
三.解答题(共7小题)
19.解:由题意得:(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形.
20.证明:∵C是AB的中点(已知),∴AC=CB(线段中点的定义).
∵CD∥BE(已知),∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,,∴△ACD≌△CBE(SAS).
21.AC=DF.
证明:∵BF=EC,∴BF﹣CF=EC﹣CF,∴BC=EF,
在△ABC和△DEF中∴△ABC≌△DEF.
22.证明:∵∠BAC=∠DAE,∴∠BAC﹣BAE=∠DAE﹣∠BAE,即∠BAD=∠CAE,
在△ABD和△AEC中,∴△ABD≌△AEC(SAS).
23.解:∵AE=CF,∴AE+EF=CF+EF,∴AF=CE,
在△ADF和△CBE中,,∴△ADF≌△CBE(ASA).
24.证明:∵AE∥CF,∴∠A=∠FCD,
在△ABE和△CDF中,,∴△ABE≌△CDF(SAS),∴∠E=∠F.
25.(1)解:如图,∵在Rt△ABC中,∠ACB=90°,∠B=30°,
∴∠B=30°,∴∠CAB=60°.
又∵AD平分∠CAB,∴∠CAD=∠CAB=30°,即∠CAD=30°;
(2)证明:∵∠ACD+∠ECD=180°,且∠ACD=90°,∴∠ECD=90°,∴∠ACD=∠ECD.
在△ACD与△ECD中,,∴△ACD≌△ECD(SAS),∴DA=DE.
一.选择题(共8小题)
1.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B. 60° C. 58° D. 50°
(1) (3) (4)
2.如果两个图形全等,则这个图形必定是( )
A.形状相同,但大小不同 B. 形状大小均相同
C.大小相同,但形状不同 D. 形状大小均不相同
3.如图,△ABC≌△DEF,则此图中相等的线段有( )
A.1对 B. 2对 C. 3对 D. 4对
4.(2013 金平区)木工师傅在做完门框后,为防止变形常常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的根据是( )
A.矩形的对称性 B. 矩形的四个角都是直角
C.三角形的稳定性 D. 两点之间线段最短
5.(2004 南山区)如图,若△ABC≌△DEF,则∠E等于( )
A.30° B. 50° C. 60° D. 100°
(5) (6) (7)
6.如图,若△ABC≌△ADE,则下列结论不正确的是( )
A.AB=AD B. AC=AD C. AC=AE D. BC=DE
7.(2014 黔西南州)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
8.(2014 塘沽区)如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.∠B=∠C B. ∠BDA=∠CDA C. AB=AC D. BD=CD
(8) (9) (10) (11)
二.填空题(共10小题)
9.(2012 沐川县)在如图所示的2×2方格中,连接AB、AC,则∠1+∠2= ___ 度.
10.如图所示的方格中,∠1+∠2+∠3= _________ 度.
11.空调安装在墙上时,一般都会象如图所示的方法固定在墙上,这种方法应用的数学知识是 _________ .
12.(2014 淮安)如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠ADC的度数为 _________ .
(12) (13) (14)
13.(2014 山西)如图,△ABC≌△DCB,AC与BD相交于点E,若∠A=∠D=80°,∠ABC=60°,则∠BEC等于 _________ .
14.(2013 柳州)如图,△ABC≌△DEF,请根据图中提供的信息,写出x= ______ .
15.(2014 牡丹江)如图,点B、E、C、F在一条直线上,AB=DE,BE=CF,请添加一个条件 _________ ,使△ABC≌△DEF.
(15) (16) (17) (18)
16.(2014 绥化)如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是 _________ (填出一个即可).
17.(2014 长沙)如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF= _________ .
18.(2013 天津)如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,请写出图中一组相等的线段 _________ .
三.解答题(共7小题)
19.找出下列图形中的全等图形.
20.(2014 常州)已知:如图,点C为AB中点,CD=BE,CD∥BE.
求证:△ACD≌△CBE.
21.(2014 漳州)如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)
22.(2014 吉林)如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,
求证:△ABD≌△AEC.
23.(2014 硚口区二模)如图,已知AE=CF,∠AFD=∠CEB,∠A=∠C,求证:△ADF≌△CBE.
24.(2014 昆明)已知:如图,点A、B、C在同一直线上,AB=CD,AE∥CF,且AE=CF.
求证:∠E=∠F.
25.(2014 宜昌)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.
鲁教版五四制初二数学第一单元1.3全等三角形对应练习参考答案
一.选择题(共8小题)
1.D.2.B.3.D.4.C.5.D.6.B.7.C.8.D.
二.填空题(共10小题)
9. 90 10. 135 11.三角形的稳定性 12. 130° 13. 100° 14. 20
15. AC=DF(或∠B=∠DEF或AB∥DE)
16.AB=CD(答案不唯一) 17. 6 18. AC=BD(答案不唯一)
三.解答题(共7小题)
19.解:由题意得:(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形.
20.证明:∵C是AB的中点(已知),∴AC=CB(线段中点的定义).
∵CD∥BE(已知),∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,,∴△ACD≌△CBE(SAS).
21.AC=DF.
证明:∵BF=EC,∴BF﹣CF=EC﹣CF,∴BC=EF,
在△ABC和△DEF中∴△ABC≌△DEF.
22.证明:∵∠BAC=∠DAE,∴∠BAC﹣BAE=∠DAE﹣∠BAE,即∠BAD=∠CAE,
在△ABD和△AEC中,∴△ABD≌△AEC(SAS).
23.解:∵AE=CF,∴AE+EF=CF+EF,∴AF=CE,
在△ADF和△CBE中,,∴△ADF≌△CBE(ASA).
24.证明:∵AE∥CF,∴∠A=∠FCD,
在△ABE和△CDF中,,∴△ABE≌△CDF(SAS),∴∠E=∠F.
25.(1)解:如图,∵在Rt△ABC中,∠ACB=90°,∠B=30°,
∴∠B=30°,∴∠CAB=60°.
又∵AD平分∠CAB,∴∠CAD=∠CAB=30°,即∠CAD=30°;
(2)证明:∵∠ACD+∠ECD=180°,且∠ACD=90°,∴∠ECD=90°,∴∠ACD=∠ECD.
在△ACD与△ECD中,,∴△ACD≌△ECD(SAS),∴DA=DE.
