北师大版数学四年级下册 第五单元 认识方程-第三课时 方程 课件(27张PPT)
文档属性
| 名称 | 北师大版数学四年级下册 第五单元 认识方程-第三课时 方程 课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 971.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-20 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
四年级数学下册教学课件(北师版)
第五单元 认识方程
第三课时 方程
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
结合下列情境说说数量间的等量关系。
(1)小芳家离学校1000米,比小明家离学校远200米。
(2)小沁今年8岁,她爸爸的年龄是她的4倍。
1000-200=小明家离学校的距离
8×4=小沁爸爸的年龄
探索与发现
02
探索与发现
知识点
方程的含义
说一说右面各图中的等量关系。
10g
2g
10克=樱桃的质量+2g
探索与发现
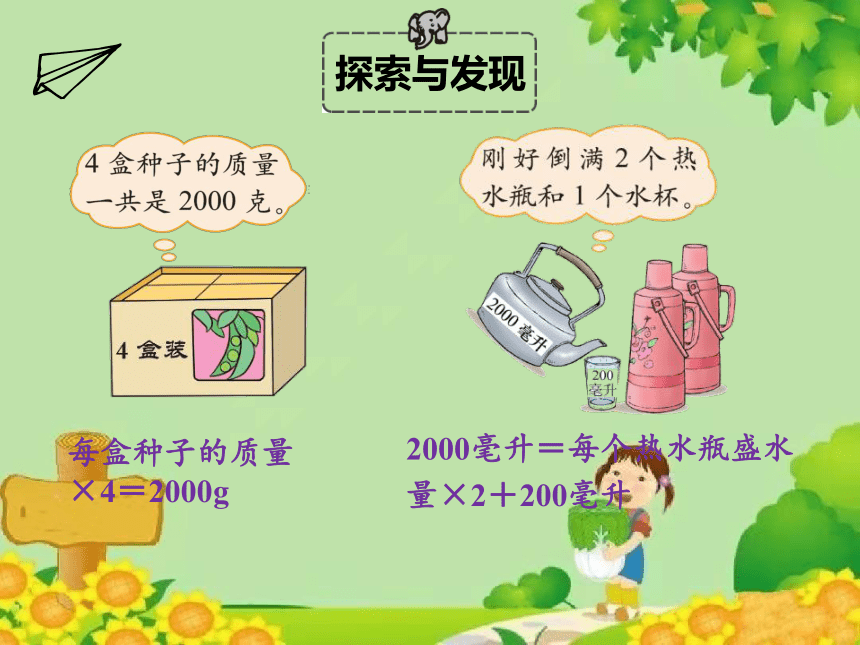
每盒种子的质量×4=2000g
2000毫升=每个热水瓶盛水量×2+200毫升
探索与发现
用x表示樱桃的质量,用式子表示天平中的等量关系。
10g
2g
10克=樱桃的质量+2g
10=x+2
探索与发现
像上面那样,表示其他情境中的等量关系。
每盒种子的质量×4=2000g
4y=2000
用y表示每盒种子的质量……
探索与发现
用z表示每个热水瓶的盛水量……
2000毫升=每个热水瓶盛水量×2+200毫升
2000=2z+200
探索与发现
这些等式有什么共同点?与同伴进行交流。
2000=2z+200
4y=2000
10=x+2
这样含有未知数的等式叫方程
探索与发现
探索与发现
知识提炼
含有未知数的等式叫方程,方程是特殊的等式,所有的方程都是等式,但等式不一定是方程。等式和方程的关系可表示为
方程
等式
探索与发现
小试牛刀
(选自教材P67 T1)先说一说各图中的等量关系,再列出方程。
(1)
(2)
x+20=70
5x+4=44
探索与发现
(3)
4x+6-3=87
(x-5)×4=2x
探索与发现
(4)
2b+15=100
学以致用
03
学以致用
1.(选自教材P67 T2)根据题意先说出等量关系再列出方程。
(1)一辆公共汽车到站时,有5人下车,8人上车,车上现有15人,车上原有x人,那么 。(2)还记得第63页摆图形的游戏吗?用95个小正方形摆出了x个大门,那么 。
x-5+8=15
5x=95
学以致用
2.(选自教材P67 T3)日历表的规律。
认真观察下图阴影方框中正中间的数与其他四个数的关系。
(1)中间数是y,左边的数是 ,右边的数是 ,上面的数是 ,下面的数是 。
y-1
y+1
y-7
y+7
学以致用
(2)方框中5个数之和与中间的数有什么关系?
(3)当5个数的和是115时,中间的数是多少?
5 个数之和是中间数的 5 倍
115÷5=23
学以致用
3.选一选。
(1)5x+8.1=18.1 是( )。
A. 等式不是方程 B. 方程
(2)下面的式子中,( )是方程。
A. 25x B. 15-3=12
C. 6x+1=6 D. 4x+7<9
B
C
学以致用
4.判断下面的式子,是方程的在括号里画“√”,不是方程的画“×”。
(1)3.6-x=0.8( )(2)4.5+x>3.4( )
(3)5x-32=46( )(4)x÷8.2=16.8( )
(5)0.2+8.8=9( )(6)6m-m=120( )
√
√
×
√
×
√
学以致用
5.看图列方程。
3x+4=40
3x+30=150
学以致用
6.你会列方程吗?(只列方程不解答)
苹果和梨的单价分别是每千克 2.5 元和1.8元,我买了 2 千克苹果和一些梨共花了10.4 元,我买了多少千克梨?
解:设买了 x 千克梨。
2.5×2+1.8x=10.4
学以致用
含有未知数的等式叫方程,方程是特殊的等式,所有的方程都是等式,但等式不一定是方程。等式和方程的关系可表示为
方程
等式
课后作业
04
感 谢 观 看
四年级数学下册教学课件(北师版)
第五单元 认识方程
第三课时 方程
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
结合下列情境说说数量间的等量关系。
(1)小芳家离学校1000米,比小明家离学校远200米。
(2)小沁今年8岁,她爸爸的年龄是她的4倍。
1000-200=小明家离学校的距离
8×4=小沁爸爸的年龄
探索与发现
02
探索与发现
知识点
方程的含义
说一说右面各图中的等量关系。
10g
2g
10克=樱桃的质量+2g
探索与发现
每盒种子的质量×4=2000g
2000毫升=每个热水瓶盛水量×2+200毫升
探索与发现
用x表示樱桃的质量,用式子表示天平中的等量关系。
10g
2g
10克=樱桃的质量+2g
10=x+2
探索与发现
像上面那样,表示其他情境中的等量关系。
每盒种子的质量×4=2000g
4y=2000
用y表示每盒种子的质量……
探索与发现
用z表示每个热水瓶的盛水量……
2000毫升=每个热水瓶盛水量×2+200毫升
2000=2z+200
探索与发现
这些等式有什么共同点?与同伴进行交流。
2000=2z+200
4y=2000
10=x+2
这样含有未知数的等式叫方程
探索与发现
探索与发现
知识提炼
含有未知数的等式叫方程,方程是特殊的等式,所有的方程都是等式,但等式不一定是方程。等式和方程的关系可表示为
方程
等式
探索与发现
小试牛刀
(选自教材P67 T1)先说一说各图中的等量关系,再列出方程。
(1)
(2)
x+20=70
5x+4=44
探索与发现
(3)
4x+6-3=87
(x-5)×4=2x
探索与发现
(4)
2b+15=100
学以致用
03
学以致用
1.(选自教材P67 T2)根据题意先说出等量关系再列出方程。
(1)一辆公共汽车到站时,有5人下车,8人上车,车上现有15人,车上原有x人,那么 。(2)还记得第63页摆图形的游戏吗?用95个小正方形摆出了x个大门,那么 。
x-5+8=15
5x=95
学以致用
2.(选自教材P67 T3)日历表的规律。
认真观察下图阴影方框中正中间的数与其他四个数的关系。
(1)中间数是y,左边的数是 ,右边的数是 ,上面的数是 ,下面的数是 。
y-1
y+1
y-7
y+7
学以致用
(2)方框中5个数之和与中间的数有什么关系?
(3)当5个数的和是115时,中间的数是多少?
5 个数之和是中间数的 5 倍
115÷5=23
学以致用
3.选一选。
(1)5x+8.1=18.1 是( )。
A. 等式不是方程 B. 方程
(2)下面的式子中,( )是方程。
A. 25x B. 15-3=12
C. 6x+1=6 D. 4x+7<9
B
C
学以致用
4.判断下面的式子,是方程的在括号里画“√”,不是方程的画“×”。
(1)3.6-x=0.8( )(2)4.5+x>3.4( )
(3)5x-32=46( )(4)x÷8.2=16.8( )
(5)0.2+8.8=9( )(6)6m-m=120( )
√
√
×
√
×
√
学以致用
5.看图列方程。
3x+4=40
3x+30=150
学以致用
6.你会列方程吗?(只列方程不解答)
苹果和梨的单价分别是每千克 2.5 元和1.8元,我买了 2 千克苹果和一些梨共花了10.4 元,我买了多少千克梨?
解:设买了 x 千克梨。
2.5×2+1.8x=10.4
学以致用
含有未知数的等式叫方程,方程是特殊的等式,所有的方程都是等式,但等式不一定是方程。等式和方程的关系可表示为
方程
等式
课后作业
04
感 谢 观 看
