2023年湖北省黄冈、孝感、咸宁中考数学全真模拟试卷(无答案)
文档属性
| 名称 | 2023年湖北省黄冈、孝感、咸宁中考数学全真模拟试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 105.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-21 20:57:31 | ||
图片预览


文档简介
2023年湖北黄冈、孝感、咸宁中考数学全真模拟试卷
(时间:120分钟 总分:120分)
一、选择题(本大题共8小题,共24分)
1.下列算式中,运算结果为负数的是( )
A.﹣(﹣2) B.|﹣2| C.﹣22 D.(﹣2)2
2.2019年被称为中国的5G元年,如果运用5G技术下载一个4.8M的短视频,大约只需要0.000096秒,将数字0.000096用科学记数法表示应为( )
A.0.96×10﹣4 B.9.6×10﹣3 C.9.6×10﹣5 D.96×10﹣6
3.如图所示的几何体的俯视图是( )
A. B. C. D.
4.下列运算正确的是( )
A.a+2a=3a2 B.a2 a3=a5 C.(ab)3=ab3 D.(﹣a3)2=﹣a6
5.如果一个三角形能够分成两个与原三角形都相似的三角形,我们把这样的三角形称为孪生三角形,那么孪生三角形是( )
A.不存在
B.等腰三角形
C.直角三角形
D.等腰三角形或直角三角形
6.如图所示,在⊙O中,线段AB是直径,点D是弧AB上一点.延长AB至点C,使得AB=2BC,连接AD,OD,CD.若∠C=30°,则∠ADO的余弦值是( )
A. B. C. D.
7.如图,在矩形ABCD中,BC=12,点E为AD的中点,点F为CD边上一点,DF=2,将线段EF绕点E顺时针旋转90°得到EH,点H恰好在线段BF上,过H作直线HM⊥AD于点M,交BC于点N,则CF的长为( )
A.2 B.5 C.6 D.8
8.如图,已知四边形OABC是平行四边形,OC:OA=4:3,CD⊥x轴,垂足为D,函数y=的图象经过点C,且与AB交于点E.若OD=2,则△BCE的面积为( )
A. B.2 C. D.
二、填空题(本大题共8小题,共24分)
9.使得二次根式有意义的x的取值范围是 .
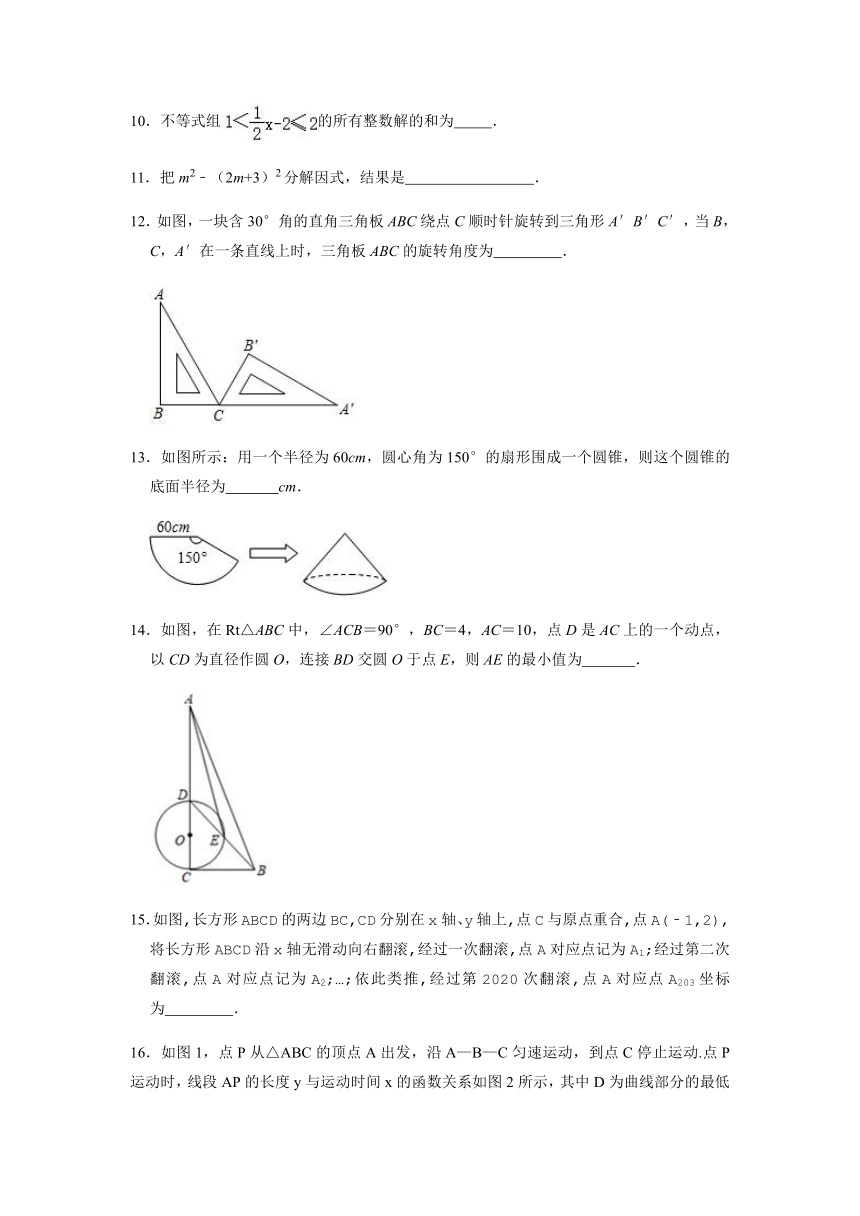
10.不等式组的所有整数解的和为 .
11.把m2﹣(2m+3)2分解因式,结果是 .
12.如图,一块含30°角的直角三角板ABC绕点C顺时针旋转到三角形A′B′C′,当B,C,A′在一条直线上时,三角板ABC的旋转角度为 .
13.如图所示:用一个半径为60cm,圆心角为150°的扇形围成一个圆锥,则这个圆锥的底面半径为 cm.
14.如图,在Rt△ABC中,∠ACB=90°,BC=4,AC=10,点D是AC上的一个动点,以CD为直径作圆O,连接BD交圆O于点E,则AE的最小值为 .
15.如图,长方形ABCD的两边BC,CD分别在x轴、y轴上,点C与原点重合,点A(﹣1,2),将长方形ABCD沿x轴无滑动向右翻滚,经过一次翻滚,点A对应点记为A1;经过第二次翻滚,点A对应点记为A2;…;依此类推,经过第2020次翻滚,点A对应点A203坐标为 .
16.如图1,点P从△ABC的顶点A出发,沿A—B—C匀速运动,到点C停止运动.点P运动时,线段AP的长度y与运动时间x的函数关系如图2所示,其中D为曲线部分的最低点,则△ABC的面积是 .
四、解答题(本大题共8小题,共72分)
17.(6分)先化简,再求值,其中x=2.
18.(8分)益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低,马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元.A,B两种产品原来的运费和现在的运费(单位:元/件)如下表所示:
品种 A B
原运费 45 25
现运费 30 20
(1)求每次运输的农产品中A,B产品各有多少件?
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的产品总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元?
19.(8分)一个不透明的口袋中装有3张卡片,卡片上分别标有数字1、﹣2、﹣3,它们除了标有的数字不同之外再也没有其它区别,小芳从盒子中随机抽取一张卡片.
(1)求小芳抽到负数的概率;
(2)若小明再从剩余的三张卡片中随机抽取一张,请你用树状图或列表法,求小明和小芳两人均抽到负数的概率.
20.(9分)如图,反比例函数y=的图象和一次函数的图象交于A、B两点,点A的横坐标和点B的纵坐标都是1.
(1)求一次函数的表达式;
(2)在第一象限内,写出关于x的不等式kx+b≥的解集 ;
(3)若点P(m,n)在反比例函数图象上,且关于y轴对称的点Q恰好落在一次函数的图象上,求m2+n2的值.
21.(9分)如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边AC上一点O为圆心,OA为半径作圆,恰好经过边BC的中点D,并与边AC相交于另一点F.
(1)求证:BD是⊙O的切线;
(2)若,点E是半圆AmF上一动点,连接AE、AD、DE,填空:
①当的长度是 时,四边形ABDE是菱形;
②当的长度是 时,△ADE是直角三角形.
22.(10分)某水果经销商以19元/千克的价格新进一批芒果进行销售,因为芒果不耐储存,在运输储存过程损耗率为5%.为了得到日销售量y(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) 20 25 30 35 40
日销售量y(千克) 400 300 200 100 0
(1)这批芒果的实际成本为______元千克;[实际成本=进价损耗率)]
(2)①请你根据表中的数据直接出写出y与x之间的函数表达式,标出x的取值范围;
②该水果经销商应该如何确定这批芒果的销售价格,才能使日销售利润W1最大?
(3)该水果经销商参与电商平台助农活动,开展网上直销,可以完全避免运输储存过程中的损耗成本,但每销售1千克芒果需支出a元的相关费用,销售量与销售价格之间关系不变.当25≤x≤29,该水果经销商日获利W2的最大值为2090元,求a的值.
23.(10分)【模型构建】如图所示,在边长为1的正方形ABCD中,△DEF的顶点E,F分别在AB,BC上(可与点A,B,C重合),且满足∠EDF=45°.△DEF的高线DG交线段EF于点G(可与E,F重合),设=k.
(1)求k的值.
【模型拓展】在【模型构建】的基础上,将条件“边长为1的正方形ABCD”改为“长AB=8、宽AD=6的矩形ABCD”(其他条件不变).
(2)判断k的值是否改变.若改变,请求出k的取值范围;若不改变,请证明.
【深入探究】在【模型构建】的基础上,设△DEF的面积为S.
(3)①求S的最小值;
②当S取到最小值时,直接写出DG与GB的数量关系.
24.(12分)如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B,与y轴交于点C,∠ABC=45°.
(1)求抛物线的解析式.
(2)过抛物线的顶点D作DH⊥x轴于E,点P为直线DH上一动点,当△PHC是等腰三角形时,求出点P的坐标.
(3)如图2,点E为第二象限抛物线上一动点,EF⊥x轴与BC交于F,求EF的最大值,并说明此时△BCE的面积是否最大.
图1 图2
(时间:120分钟 总分:120分)
一、选择题(本大题共8小题,共24分)
1.下列算式中,运算结果为负数的是( )
A.﹣(﹣2) B.|﹣2| C.﹣22 D.(﹣2)2
2.2019年被称为中国的5G元年,如果运用5G技术下载一个4.8M的短视频,大约只需要0.000096秒,将数字0.000096用科学记数法表示应为( )
A.0.96×10﹣4 B.9.6×10﹣3 C.9.6×10﹣5 D.96×10﹣6
3.如图所示的几何体的俯视图是( )
A. B. C. D.
4.下列运算正确的是( )
A.a+2a=3a2 B.a2 a3=a5 C.(ab)3=ab3 D.(﹣a3)2=﹣a6
5.如果一个三角形能够分成两个与原三角形都相似的三角形,我们把这样的三角形称为孪生三角形,那么孪生三角形是( )
A.不存在
B.等腰三角形
C.直角三角形
D.等腰三角形或直角三角形
6.如图所示,在⊙O中,线段AB是直径,点D是弧AB上一点.延长AB至点C,使得AB=2BC,连接AD,OD,CD.若∠C=30°,则∠ADO的余弦值是( )
A. B. C. D.
7.如图,在矩形ABCD中,BC=12,点E为AD的中点,点F为CD边上一点,DF=2,将线段EF绕点E顺时针旋转90°得到EH,点H恰好在线段BF上,过H作直线HM⊥AD于点M,交BC于点N,则CF的长为( )
A.2 B.5 C.6 D.8
8.如图,已知四边形OABC是平行四边形,OC:OA=4:3,CD⊥x轴,垂足为D,函数y=的图象经过点C,且与AB交于点E.若OD=2,则△BCE的面积为( )
A. B.2 C. D.
二、填空题(本大题共8小题,共24分)
9.使得二次根式有意义的x的取值范围是 .
10.不等式组的所有整数解的和为 .
11.把m2﹣(2m+3)2分解因式,结果是 .
12.如图,一块含30°角的直角三角板ABC绕点C顺时针旋转到三角形A′B′C′,当B,C,A′在一条直线上时,三角板ABC的旋转角度为 .
13.如图所示:用一个半径为60cm,圆心角为150°的扇形围成一个圆锥,则这个圆锥的底面半径为 cm.
14.如图,在Rt△ABC中,∠ACB=90°,BC=4,AC=10,点D是AC上的一个动点,以CD为直径作圆O,连接BD交圆O于点E,则AE的最小值为 .
15.如图,长方形ABCD的两边BC,CD分别在x轴、y轴上,点C与原点重合,点A(﹣1,2),将长方形ABCD沿x轴无滑动向右翻滚,经过一次翻滚,点A对应点记为A1;经过第二次翻滚,点A对应点记为A2;…;依此类推,经过第2020次翻滚,点A对应点A203坐标为 .
16.如图1,点P从△ABC的顶点A出发,沿A—B—C匀速运动,到点C停止运动.点P运动时,线段AP的长度y与运动时间x的函数关系如图2所示,其中D为曲线部分的最低点,则△ABC的面积是 .
四、解答题(本大题共8小题,共72分)
17.(6分)先化简,再求值,其中x=2.
18.(8分)益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低,马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元.A,B两种产品原来的运费和现在的运费(单位:元/件)如下表所示:
品种 A B
原运费 45 25
现运费 30 20
(1)求每次运输的农产品中A,B产品各有多少件?
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的产品总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元?
19.(8分)一个不透明的口袋中装有3张卡片,卡片上分别标有数字1、﹣2、﹣3,它们除了标有的数字不同之外再也没有其它区别,小芳从盒子中随机抽取一张卡片.
(1)求小芳抽到负数的概率;
(2)若小明再从剩余的三张卡片中随机抽取一张,请你用树状图或列表法,求小明和小芳两人均抽到负数的概率.
20.(9分)如图,反比例函数y=的图象和一次函数的图象交于A、B两点,点A的横坐标和点B的纵坐标都是1.
(1)求一次函数的表达式;
(2)在第一象限内,写出关于x的不等式kx+b≥的解集 ;
(3)若点P(m,n)在反比例函数图象上,且关于y轴对称的点Q恰好落在一次函数的图象上,求m2+n2的值.
21.(9分)如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边AC上一点O为圆心,OA为半径作圆,恰好经过边BC的中点D,并与边AC相交于另一点F.
(1)求证:BD是⊙O的切线;
(2)若,点E是半圆AmF上一动点,连接AE、AD、DE,填空:
①当的长度是 时,四边形ABDE是菱形;
②当的长度是 时,△ADE是直角三角形.
22.(10分)某水果经销商以19元/千克的价格新进一批芒果进行销售,因为芒果不耐储存,在运输储存过程损耗率为5%.为了得到日销售量y(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) 20 25 30 35 40
日销售量y(千克) 400 300 200 100 0
(1)这批芒果的实际成本为______元千克;[实际成本=进价损耗率)]
(2)①请你根据表中的数据直接出写出y与x之间的函数表达式,标出x的取值范围;
②该水果经销商应该如何确定这批芒果的销售价格,才能使日销售利润W1最大?
(3)该水果经销商参与电商平台助农活动,开展网上直销,可以完全避免运输储存过程中的损耗成本,但每销售1千克芒果需支出a元的相关费用,销售量与销售价格之间关系不变.当25≤x≤29,该水果经销商日获利W2的最大值为2090元,求a的值.
23.(10分)【模型构建】如图所示,在边长为1的正方形ABCD中,△DEF的顶点E,F分别在AB,BC上(可与点A,B,C重合),且满足∠EDF=45°.△DEF的高线DG交线段EF于点G(可与E,F重合),设=k.
(1)求k的值.
【模型拓展】在【模型构建】的基础上,将条件“边长为1的正方形ABCD”改为“长AB=8、宽AD=6的矩形ABCD”(其他条件不变).
(2)判断k的值是否改变.若改变,请求出k的取值范围;若不改变,请证明.
【深入探究】在【模型构建】的基础上,设△DEF的面积为S.
(3)①求S的最小值;
②当S取到最小值时,直接写出DG与GB的数量关系.
24.(12分)如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B,与y轴交于点C,∠ABC=45°.
(1)求抛物线的解析式.
(2)过抛物线的顶点D作DH⊥x轴于E,点P为直线DH上一动点,当△PHC是等腰三角形时,求出点P的坐标.
(3)如图2,点E为第二象限抛物线上一动点,EF⊥x轴与BC交于F,求EF的最大值,并说明此时△BCE的面积是否最大.
图1 图2
同课章节目录
