5.1 曲线运动 5.2运动的合成与分解 课件 -2022-2023学年高一下学期物理人教版(2019)必修第二册(共29张PPT)
文档属性
| 名称 | 5.1 曲线运动 5.2运动的合成与分解 课件 -2022-2023学年高一下学期物理人教版(2019)必修第二册(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-20 21:40:13 | ||
图片预览






文档简介
(共29张PPT)
5.1
曲线运动
生活中的曲线运动:
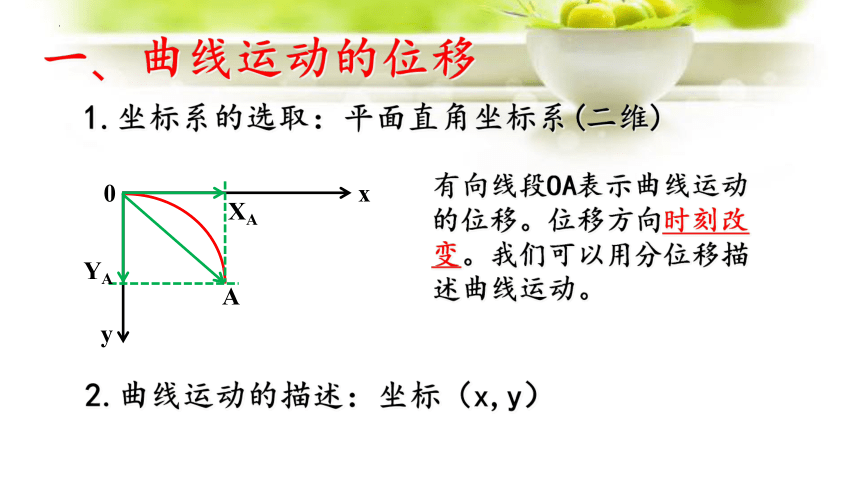
一、曲线运动的位移
1.坐标系的选取:平面直角坐标系(二维)
2.曲线运动的描述:坐标(x,y)
0
x
y
A
有向线段OA表示曲线运动的位移。位移方向时刻改变。我们可以用分位移描述曲线运动。
XA
YA
二、曲线运动的速度
火星由于惯性,以脱离砂轮时的速度沿切线方向飞出,切线方向即为火星飞出时的速度方向
水滴沿伞边缘的切线方向飞出。
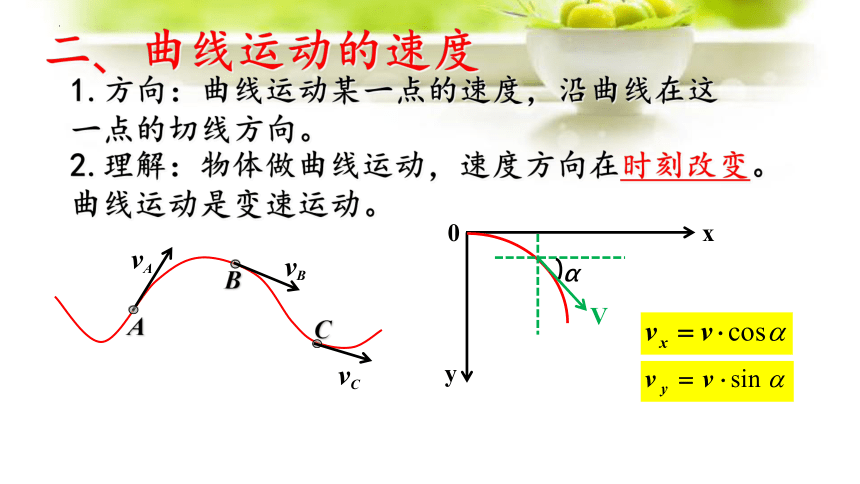
1.方向:曲线运动某一点的速度,沿曲线在这一点的切线方向。
2.理解:物体做曲线运动,速度方向在时刻改变。曲线运动是变速运动。
vA
A
B
C
vB
vC
二、曲线运动的速度
0
x
y
V
α
O
A
B
合运动
X
Y
V
Vx
Vy
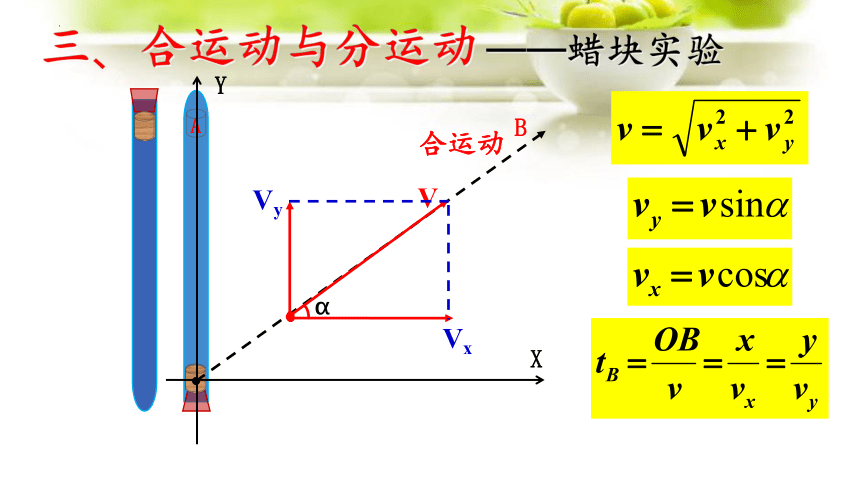
三、合运动与分运动
α
——蜡块实验
1.合运动与分运动:若物体同时参与几个运动,它的实际运动称为合运动,参与的几个运动称为分运动。
2.理解:
(1)等时性:分运动与合运动同时发生;
(2)等效性:运动效果相同;
(3)独立性:分运动之间互不干扰;
四、物体做曲线运动的条件
1.条件:物体受到的合外力与运动方向不共线。
F合或 a 跟 v 在同一直线上
直线运动
a 恒定→匀变速直线运动
a 变化→变加速直线运动
F合或 a 跟 v 不在同一直线上
曲线运动
a 恒定→匀变速曲线运动
a 变化→变加速曲线运动
思考1:
做曲线运动的物体运动轨迹、速度方向与其所受合外力方向三者位置关系如何?
G
v1
G
G
v2
v3
v
F
物体运动轨迹夹在速度方向和合外力方向之间。
做曲线运动的物体运动轨迹弯曲方向与其所受合外力方向有什么关系呢?
思考2:
G
v1
G
G
v2
v3
v
F
做曲线运动的物体所受合外力必指向运动轨迹凹的一侧。
2.特点:做曲线运动的物体,受到的合外力与速度在轨迹的两侧;且轨迹向受力方向弯曲。
题型:小船过河问题(运动的合成与分解)
1.三种速度:
船速V静(船在静水中的速度);
水流的速度V水;
船的实际运动速度V。
2.船的实际运动,是水流的运动和船在静水中运动的合运动。
d
分析:欲使船渡河时间最短,船头的方向应该垂直于河岸。
问题1:求小船过河的最短时间。
A
θ
d
设船头指向与上游河岸成θ:
结论:当v静>v水时,最短位移等于河宽d。
问题2:求小船过河的最短位移
A
以v水矢量末端为圆心,以v静矢量的大小为半径画圆,从v水的始端向圆弧作切线,则合速度沿此切线方向航程最短.
θ
θ
结论:当v静< v水时,最短航程不等于河宽d。
船头指向与上游河岸成θ:
θ
θ
d
Xmin
如图所示,河宽200 m,一条小船要将货物从A点运送到河对岸的B点,已知AB连线与河岸的夹角θ=30°,河水的流速v水=5 m/s,小船在静水中的速度至少是( )A.2.5m/s B.3.0m/s C.5.0m/s D.4.0m/s
A
如图所示,甲、乙两船在同一条河流中同时渡河,河的宽度为L,河水流速为u,划船速度均为v,出发时两船相距2L,甲、乙船头均与岸边成60°角,且乙船恰好能直达正对岸的点,则下列判断正确的是( )
A.甲、乙两船到达对岸的时间相等
B.两船可能在未到达对岸前相遇
C.甲船在A点左侧靠岸
D.甲船也在A点靠岸
AC
题型:关联速度问题
例.如图所示,物体放在水平平台上,系在物体上的绳子跨过定滑轮,由地面上的人以速度向右水平匀速拉动,设人从地面上平台的边缘开始向右行至绳与水平方向夹角为30°处,此时物体的速度为( )
A. B.
C. D.
C
绳下端实际速度
1.使下端绳子伸长
2.使下端绳子旋转
将沿绳方向分解为
将沿垂直于绳方向分解为
绳上端实际速度
使上端绳子缩短
作用效果
绳子下端伸长的速度和上端缩短的速度大小相等,即
因此
故本题选C.
例.一根细绳通过定滑轮且两端分别系着A和B两物体,如图所示,物体A在外力作用下,向左以vA匀速运动,当连A的绳子与水平方向成a角,连B的绳子与水平方向成角时,B物体的速度为vB,则( )
A.A物体的速度vA与B物体的速度vB的大小相等
B.A物体的速度vA与B物体的速度vB的大小关系满足
C.此后B物体以速度vB做匀速运动
D.此后B物体的速度越来越大,所以做减速运动
B
绳A端实际速度
1.使A端绳子伸长
2.使A端绳子旋转
将沿绳方向分解为
将沿垂直于绳方向分解为
绳B端实际速度
1.使B端绳子缩短
作用效果
作用效果
绳子A端伸长的速度和B端缩短的速度大小相等,即
因此=
故本题选B.
2.使B端绳子旋转
将沿绳方向分解为
将沿垂直于绳方向分解为
例.如图所示,一根铁棒AB两端分别沿竖直墙壁和水平地面滑动,当铁棒滑到与竖直墙壁成θ角时,A端下滑的速度为v,则此时B端移动的速度为( )
A.vsinθ B. C.vtanθ D.
D
例3.如图所示,一根铁棒AB两端分别沿竖直墙壁和水平地面滑动,当铁棒滑到与竖直墙壁成θ角时,A端下滑的速度为v,则此时B端移动的速度为( )
A.vsinθ B. C.vtanθ D.
有:
故选D
运动过程中,绳、杆等有长度的物体,其两端点的速度通常是不一样的,但两端点的速度是有联系的,我们称之为“关联速度”,解决关联速度的关键 :
(1)物体的实际运动(速度)一定是合运动(速度),分速度的方向要按实际运动效果确定。即一般分解时两个分速度方向应取沿绳(或杆)方向和垂直绳(或杆)方向.
(2)由于绳(或杆)不可伸长,沿绳(或杆)方向的分速度大小相等.
5.1
曲线运动
生活中的曲线运动:
一、曲线运动的位移
1.坐标系的选取:平面直角坐标系(二维)
2.曲线运动的描述:坐标(x,y)
0
x
y
A
有向线段OA表示曲线运动的位移。位移方向时刻改变。我们可以用分位移描述曲线运动。
XA
YA
二、曲线运动的速度
火星由于惯性,以脱离砂轮时的速度沿切线方向飞出,切线方向即为火星飞出时的速度方向
水滴沿伞边缘的切线方向飞出。
1.方向:曲线运动某一点的速度,沿曲线在这一点的切线方向。
2.理解:物体做曲线运动,速度方向在时刻改变。曲线运动是变速运动。
vA
A
B
C
vB
vC
二、曲线运动的速度
0
x
y
V
α
O
A
B
合运动
X
Y
V
Vx
Vy
三、合运动与分运动
α
——蜡块实验
1.合运动与分运动:若物体同时参与几个运动,它的实际运动称为合运动,参与的几个运动称为分运动。
2.理解:
(1)等时性:分运动与合运动同时发生;
(2)等效性:运动效果相同;
(3)独立性:分运动之间互不干扰;
四、物体做曲线运动的条件
1.条件:物体受到的合外力与运动方向不共线。
F合或 a 跟 v 在同一直线上
直线运动
a 恒定→匀变速直线运动
a 变化→变加速直线运动
F合或 a 跟 v 不在同一直线上
曲线运动
a 恒定→匀变速曲线运动
a 变化→变加速曲线运动
思考1:
做曲线运动的物体运动轨迹、速度方向与其所受合外力方向三者位置关系如何?
G
v1
G
G
v2
v3
v
F
物体运动轨迹夹在速度方向和合外力方向之间。
做曲线运动的物体运动轨迹弯曲方向与其所受合外力方向有什么关系呢?
思考2:
G
v1
G
G
v2
v3
v
F
做曲线运动的物体所受合外力必指向运动轨迹凹的一侧。
2.特点:做曲线运动的物体,受到的合外力与速度在轨迹的两侧;且轨迹向受力方向弯曲。
题型:小船过河问题(运动的合成与分解)
1.三种速度:
船速V静(船在静水中的速度);
水流的速度V水;
船的实际运动速度V。
2.船的实际运动,是水流的运动和船在静水中运动的合运动。
d
分析:欲使船渡河时间最短,船头的方向应该垂直于河岸。
问题1:求小船过河的最短时间。
A
θ
d
设船头指向与上游河岸成θ:
结论:当v静>v水时,最短位移等于河宽d。
问题2:求小船过河的最短位移
A
以v水矢量末端为圆心,以v静矢量的大小为半径画圆,从v水的始端向圆弧作切线,则合速度沿此切线方向航程最短.
θ
θ
结论:当v静< v水时,最短航程不等于河宽d。
船头指向与上游河岸成θ:
θ
θ
d
Xmin
如图所示,河宽200 m,一条小船要将货物从A点运送到河对岸的B点,已知AB连线与河岸的夹角θ=30°,河水的流速v水=5 m/s,小船在静水中的速度至少是( )A.2.5m/s B.3.0m/s C.5.0m/s D.4.0m/s
A
如图所示,甲、乙两船在同一条河流中同时渡河,河的宽度为L,河水流速为u,划船速度均为v,出发时两船相距2L,甲、乙船头均与岸边成60°角,且乙船恰好能直达正对岸的点,则下列判断正确的是( )
A.甲、乙两船到达对岸的时间相等
B.两船可能在未到达对岸前相遇
C.甲船在A点左侧靠岸
D.甲船也在A点靠岸
AC
题型:关联速度问题
例.如图所示,物体放在水平平台上,系在物体上的绳子跨过定滑轮,由地面上的人以速度向右水平匀速拉动,设人从地面上平台的边缘开始向右行至绳与水平方向夹角为30°处,此时物体的速度为( )
A. B.
C. D.
C
绳下端实际速度
1.使下端绳子伸长
2.使下端绳子旋转
将沿绳方向分解为
将沿垂直于绳方向分解为
绳上端实际速度
使上端绳子缩短
作用效果
绳子下端伸长的速度和上端缩短的速度大小相等,即
因此
故本题选C.
例.一根细绳通过定滑轮且两端分别系着A和B两物体,如图所示,物体A在外力作用下,向左以vA匀速运动,当连A的绳子与水平方向成a角,连B的绳子与水平方向成角时,B物体的速度为vB,则( )
A.A物体的速度vA与B物体的速度vB的大小相等
B.A物体的速度vA与B物体的速度vB的大小关系满足
C.此后B物体以速度vB做匀速运动
D.此后B物体的速度越来越大,所以做减速运动
B
绳A端实际速度
1.使A端绳子伸长
2.使A端绳子旋转
将沿绳方向分解为
将沿垂直于绳方向分解为
绳B端实际速度
1.使B端绳子缩短
作用效果
作用效果
绳子A端伸长的速度和B端缩短的速度大小相等,即
因此=
故本题选B.
2.使B端绳子旋转
将沿绳方向分解为
将沿垂直于绳方向分解为
例.如图所示,一根铁棒AB两端分别沿竖直墙壁和水平地面滑动,当铁棒滑到与竖直墙壁成θ角时,A端下滑的速度为v,则此时B端移动的速度为( )
A.vsinθ B. C.vtanθ D.
D
例3.如图所示,一根铁棒AB两端分别沿竖直墙壁和水平地面滑动,当铁棒滑到与竖直墙壁成θ角时,A端下滑的速度为v,则此时B端移动的速度为( )
A.vsinθ B. C.vtanθ D.
有:
故选D
运动过程中,绳、杆等有长度的物体,其两端点的速度通常是不一样的,但两端点的速度是有联系的,我们称之为“关联速度”,解决关联速度的关键 :
(1)物体的实际运动(速度)一定是合运动(速度),分速度的方向要按实际运动效果确定。即一般分解时两个分速度方向应取沿绳(或杆)方向和垂直绳(或杆)方向.
(2)由于绳(或杆)不可伸长,沿绳(或杆)方向的分速度大小相等.
