6.4 生活中的圆周运动 课件 -2022-2023学年高一下学期物理人教版(2019)必修第二册(共18张PPT)
文档属性
| 名称 | 6.4 生活中的圆周运动 课件 -2022-2023学年高一下学期物理人教版(2019)必修第二册(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-20 21:41:31 | ||
图片预览





文档简介
(共18张PPT)
6.4
生活中的圆周运动
一、铁路的弯道
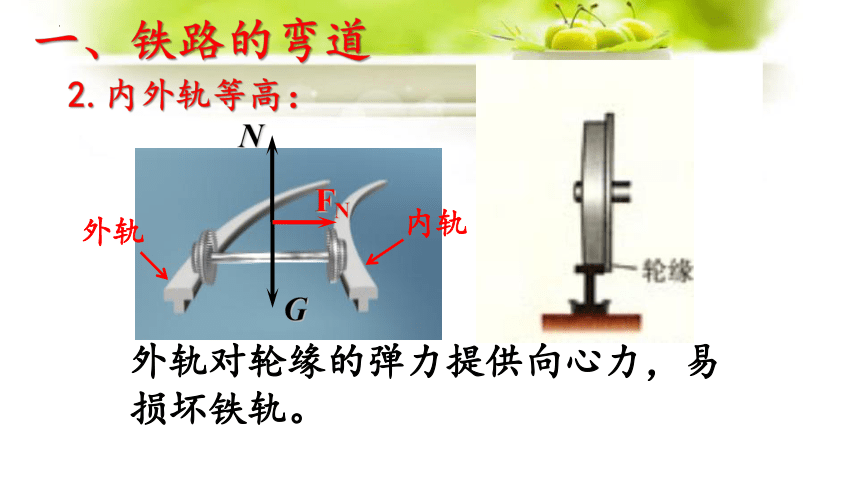
1.车轮的构造:
轮缘
外轨对轮缘的弹力提供向心力,易损坏铁轨。
N
G
FN
2.内外轨等高:
外轨
内轨
一、铁路的弯道
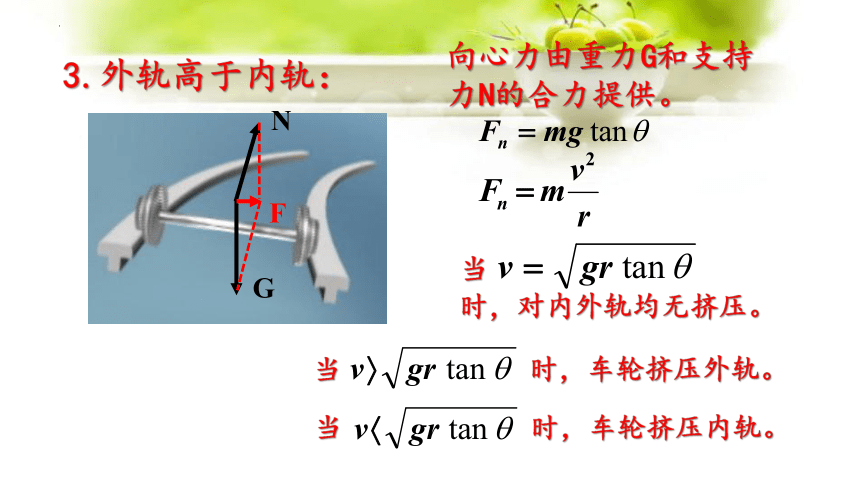
3.外轨高于内轨:
向心力由重力G和支持力N的合力提供。
G
N
F
时,对内外轨均无挤压。
当
当 时,车轮挤压外轨。
当 时,车轮挤压内轨。
生活中的类似问题:
F压=FN=mg
水平桥
拱形桥
凹形桥
二、过桥问题
汽车通过拱形桥最高点时,对桥面的压力大小?
汽车通过凹形桥最高点时,对桥面的压力大小?
汽车质量为m,通过桥最高点速度为v,桥半径为R,则在最高点汽车对桥的压力为多少?
mg
FN
FN<mg ,失重状态
若汽车通过拱桥的速度增大,会出现什么情况?
过桥问题——拱形桥
解:
由牛顿第三定律得
v2
R
mg=m
mg
FN
当FN =0 时,出现飞车现象,汽车做平抛运动,汽车及其中的物体处于完全失重状态。
v= gR
v2
R
FN =mg-m
过桥问题——拱形桥
汽车质量为m,通过桥最低点速度为v,桥半径为R,则在最低点汽车对桥的压力为多少?
解:F合=FN-mg
v2
R
∴ FN =mg + m
由牛顿第三定律得
v2
R
F压=mg + m
v2
R
∴ FN-mg=m
FN >mg 超重状态
FN
mg
Fn= m
v2
R
过桥问题——凹形桥
地球其实是一个大拱桥。
v2
R
FN =mg-m
当速度增大到一定值的时候,支持力等于0。
v2
R
mg=m
v= gR
三、离心运动
1.定义:做圆周运动的物体,某一时刻向心力突然消失或合外力不足以提供向心力,则物体会做远离圆心的运动。
2.合外力与向心力:
F=man时,物体做匀速圆周运动;
Fman时,物体做离心运动;
Fman时,物体做近心运动;
某同学用长0.8 m的细绳一端系住一个碗,碗内盛水,碗和水的总质量为0.5 kg.该同学抓住细绳另一端甩动细绳,使碗和水在竖直面内旋转.(g取10 m/s2)
(1)为了不让水从碗内洒出来,碗到最高点时的速度至少是多少?
(2)由于绳子能够承受的最大拉力为15 N,碗到最低点的速度最大不能超过多少?
解:(1)
(2)
如图所示,质量m=1 kg的小球用细线拴住,线长L=1 m,细线所受拉力达到F=19 N时就会被拉断.当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断.若此时小球距水平地面的高度h=5 m,重力加速度g取10 m/s2,求小球落地处与地面上P点的距离。
(多选)长度为L的轻杆一端固定在O点,另一端连接一小球.现使小球和轻杆在竖直平面内绕杆的固定端O转动,如图甲所示.小球做圆周运动过最高点时,杆与小球间的弹力大小用F表示,速度大小用v表示,当小球以不同速度经过最高点时,其图像如图乙所示,则( )
A.小球的质量为B.当地的重力加速度大小为C.当v2=c时,杆对小球弹力方向向上D.当v2=2b时,小球受到的弹力与重
力大小相等
甲
乙
AD
有一种杂技表演叫“飞车走壁”,由杂技演员驾驶摩托车沿光滑圆形表演台的侧壁高速行驶,在水平面内做匀速圆周运动.图中粗线圆表示摩托车的行驶轨迹,轨迹离地面的高度为h.如果增大高度h,则下列关于摩托车的说法正确的是( )
A.对侧壁的压力FN增大
B.做圆周运动的周期T不变
C.做圆周运动的向心力F增大
D.做圆周运动的线速度v增大
D
如图所示,半径为R、内径很小的光滑半圆细管竖直放置,两个质量均为m的小球A、B以不同的速率进入管内,若A球通过圆周最高点C时对管壁上部的压力为3mg(g为重力加速度),B球通过最高点C时对管壁下部的压力为0.75mg,求A、B两球落地点间的距离.(不计一切阻力)
如图所示,在光滑的圆锥顶用长为L的轻质细线悬挂一可视为质点的质量为m的小球。圆锥体轴线AB沿竖直方向,母线与轴线之间的夹角为θ=37 ,若物体跟随圆锥体且绕轴线AB做水平面内的圆周运动,已知重力加速度为g。sinθ=0.6,cosθ=0.8,求:
(1)当 时,求线对物体的拉力大小;
(2)当 时,求线对物体的拉力大小。
解:(1)
(2)
6.4
生活中的圆周运动
一、铁路的弯道
1.车轮的构造:
轮缘
外轨对轮缘的弹力提供向心力,易损坏铁轨。
N
G
FN
2.内外轨等高:
外轨
内轨
一、铁路的弯道
3.外轨高于内轨:
向心力由重力G和支持力N的合力提供。
G
N
F
时,对内外轨均无挤压。
当
当 时,车轮挤压外轨。
当 时,车轮挤压内轨。
生活中的类似问题:
F压=FN=mg
水平桥
拱形桥
凹形桥
二、过桥问题
汽车通过拱形桥最高点时,对桥面的压力大小?
汽车通过凹形桥最高点时,对桥面的压力大小?
汽车质量为m,通过桥最高点速度为v,桥半径为R,则在最高点汽车对桥的压力为多少?
mg
FN
FN<mg ,失重状态
若汽车通过拱桥的速度增大,会出现什么情况?
过桥问题——拱形桥
解:
由牛顿第三定律得
v2
R
mg=m
mg
FN
当FN =0 时,出现飞车现象,汽车做平抛运动,汽车及其中的物体处于完全失重状态。
v= gR
v2
R
FN =mg-m
过桥问题——拱形桥
汽车质量为m,通过桥最低点速度为v,桥半径为R,则在最低点汽车对桥的压力为多少?
解:F合=FN-mg
v2
R
∴ FN =mg + m
由牛顿第三定律得
v2
R
F压=mg + m
v2
R
∴ FN-mg=m
FN >mg 超重状态
FN
mg
Fn= m
v2
R
过桥问题——凹形桥
地球其实是一个大拱桥。
v2
R
FN =mg-m
当速度增大到一定值的时候,支持力等于0。
v2
R
mg=m
v= gR
三、离心运动
1.定义:做圆周运动的物体,某一时刻向心力突然消失或合外力不足以提供向心力,则物体会做远离圆心的运动。
2.合外力与向心力:
F=man时,物体做匀速圆周运动;
Fman时,物体做离心运动;
Fman时,物体做近心运动;
某同学用长0.8 m的细绳一端系住一个碗,碗内盛水,碗和水的总质量为0.5 kg.该同学抓住细绳另一端甩动细绳,使碗和水在竖直面内旋转.(g取10 m/s2)
(1)为了不让水从碗内洒出来,碗到最高点时的速度至少是多少?
(2)由于绳子能够承受的最大拉力为15 N,碗到最低点的速度最大不能超过多少?
解:(1)
(2)
如图所示,质量m=1 kg的小球用细线拴住,线长L=1 m,细线所受拉力达到F=19 N时就会被拉断.当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断.若此时小球距水平地面的高度h=5 m,重力加速度g取10 m/s2,求小球落地处与地面上P点的距离。
(多选)长度为L的轻杆一端固定在O点,另一端连接一小球.现使小球和轻杆在竖直平面内绕杆的固定端O转动,如图甲所示.小球做圆周运动过最高点时,杆与小球间的弹力大小用F表示,速度大小用v表示,当小球以不同速度经过最高点时,其图像如图乙所示,则( )
A.小球的质量为B.当地的重力加速度大小为C.当v2=c时,杆对小球弹力方向向上D.当v2=2b时,小球受到的弹力与重
力大小相等
甲
乙
AD
有一种杂技表演叫“飞车走壁”,由杂技演员驾驶摩托车沿光滑圆形表演台的侧壁高速行驶,在水平面内做匀速圆周运动.图中粗线圆表示摩托车的行驶轨迹,轨迹离地面的高度为h.如果增大高度h,则下列关于摩托车的说法正确的是( )
A.对侧壁的压力FN增大
B.做圆周运动的周期T不变
C.做圆周运动的向心力F增大
D.做圆周运动的线速度v增大
D
如图所示,半径为R、内径很小的光滑半圆细管竖直放置,两个质量均为m的小球A、B以不同的速率进入管内,若A球通过圆周最高点C时对管壁上部的压力为3mg(g为重力加速度),B球通过最高点C时对管壁下部的压力为0.75mg,求A、B两球落地点间的距离.(不计一切阻力)
如图所示,在光滑的圆锥顶用长为L的轻质细线悬挂一可视为质点的质量为m的小球。圆锥体轴线AB沿竖直方向,母线与轴线之间的夹角为θ=37 ,若物体跟随圆锥体且绕轴线AB做水平面内的圆周运动,已知重力加速度为g。sinθ=0.6,cosθ=0.8,求:
(1)当 时,求线对物体的拉力大小;
(2)当 时,求线对物体的拉力大小。
解:(1)
(2)
