8.1 功与功率 课件-2022-2023学年高一下学期物理人教版(2019)必修第二册(共40张PPT)
文档属性
| 名称 | 8.1 功与功率 课件-2022-2023学年高一下学期物理人教版(2019)必修第二册(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-20 21:50:51 | ||
图片预览








文档简介
(共40张PPT)
8.1
功与功率
詹姆斯·普雷斯科特·焦耳
詹姆斯·普雷斯科特·焦耳(1818年12月24日-1889年10月11日),英国物理学家,出生于曼彻斯特近郊的沙弗特,由于他在热学、热力学和电方面的贡献,皇家学会授予他最高荣誉的科普利奖章。后人为了纪念他,把能量或功的单位命名为“焦耳”,简称“焦”;并用焦耳姓氏的第一个字母“J”来标记。
重力势能增大
动能增大
弹性势能增大
如果物体在力的作用下能量发生了变化,则这个力一定对物体做了功。
思考:只要有力作用在物体上,这个力就会对物体做功吗
纹丝不动!!
搬不起來超重的金砖
匀速前进
思考:有力,物体也发生了位移,力会对物体做功吗?
参赛者拉着庞大的飞机缓慢前进
归纳:做功的两个必要条件 缺一不可 !
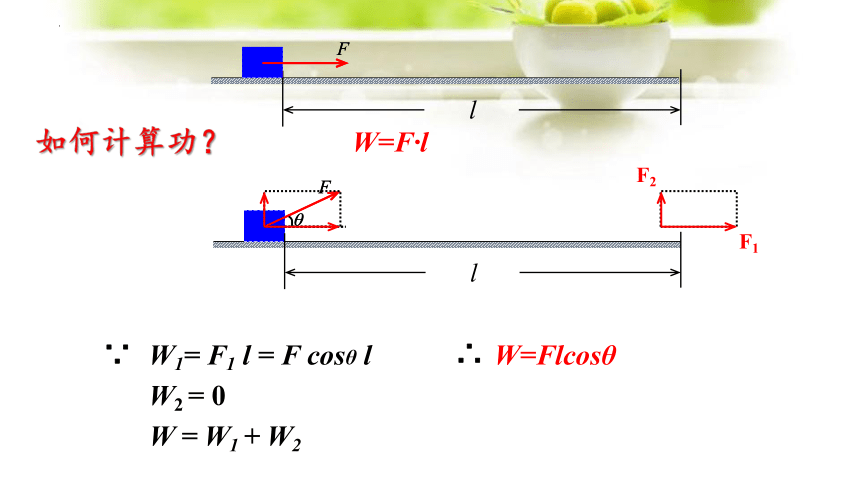
W=F·l
如何计算功?
W=Flcosθ
F1
F2
∵
W1= F1 l = F cosθ l
W2 = 0
W = W1 + W2
∴
一、功
1、概念:物体在力的作用下沿力的方向发生一段位移,则该
力对物体做功。
2、做功条件:①力;②力的方向上的位移
4、单位:
N·m
国际单位:焦耳(J)
1J=1N·m
1J等于1N的力使物体在力的方向上发生1m的位移时所做的功。
5、注意:
(1)公式只适用于恒力做功。即力的大小和方
向恒定且受力物体沿着确定直线运动。
(2)功是标量,只有大小,没有方向,但是有正负。
3、公式:
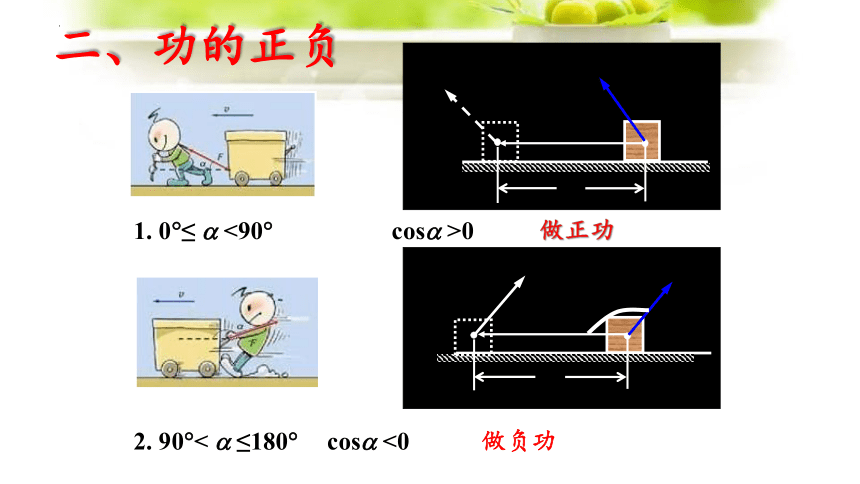
1. 0 ≤ <90 cos >0 做正功
2. 90 < ≤180 cos <0 做负功
F
F
l
F
l
F
二、功的正负
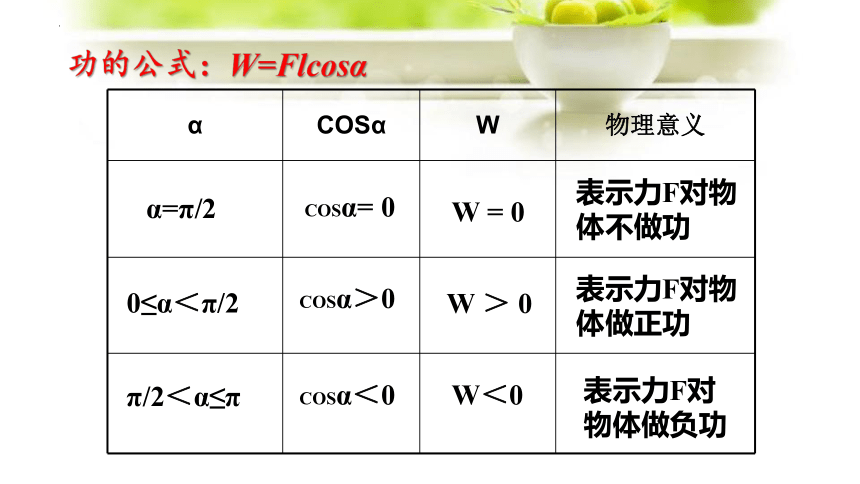
功的公式:W=Flcosα
α COSα W 物理意义
α=π/2
0≤α<π/2
π/2<α≤π
COSα= 0
COSα>0
COSα<0
W = 0
W > 0
W<0
表示力F对物体不做功
表示力F对物体做正功
表示力F对物体做负功
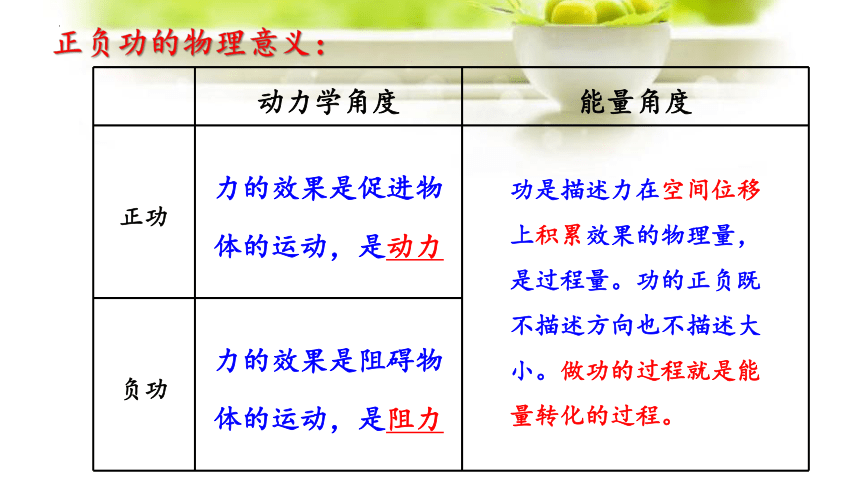
正负功的物理意义:
动力学角度 能量角度
正功 力的效果是促进物 体的运动,是动力 功是描述力在空间位移
上积累效果的物理量,
是过程量。功的正负既
不描述方向也不描述大
小。做功的过程就是能
量转化的过程。
负功 力的效果是阻碍物 体的运动,是阻力
(1)、分别求出每个力所做的功,然后求出所有功的代数和。
即:W总=W1+W2+……+Wn
(2)、先求出物体所受的合力,然后再求出合力的功,
即:W总=F合Lcosα
求力对物体所做的总功有两种方法:
三、总功
一个质量m=150kg的雪橇,受到与水平方向成θ=37°角斜向上方的拉力F=500N,在水平地面上移动的距离L=5m。物体与地面间的滑动摩擦力F阻=100N。求外力对物体所做的总功。
mg
法1:解:对物体受力分析如图所示,建立沿位移方向的坐标系,把力F分解,因此,合外力的总功为
W=(Fcosθ-f )L
=(500×0.8-100)×5J
=1500J
θ
F
f
mg
FN
解析:拉力F对物体所做的功为
W1= Flcos37°=2000J。
摩擦力F阻对物体所做的功为
W2= F阻lcos180°= -500J。
外力对物体所做的总功
W=W1+W2=1500J。
四、功率
1.定义:一个力所做的功与完成这些功所用时间的比值。
2.公式:
3.物理意义:功率是表示物体做功快慢的物理量。
4.单位:
J/s
瓦特(w)
1w=1J/s=1N·m/s
常用单位——千瓦(kw) 1kw=103w
1马力=735w
5.标矢性:功率是标量。
长时间运动时人的功率为数十瓦,优秀运动员可达1kW
长时间运动马的功率为数百瓦
鱼游动时功率可达350kW
小汽车的功率为数十千瓦至两百千瓦
高速列车的功率可达数万kW
万吨豪华游轮的功率可达数万kW
生活中的功率:
例:一个物体在水平恒力F的作用下,以速度v匀速直线运动了一段时间t,在这段时间t内F做功的功率多大
S
例:如图所示,位于水平面上的物体A,在斜向上的恒定拉力作用下,正以v=2m/s的速度向右做匀速直线运动。已知F的大小为100N,方向与速度v的夹角为37°,求:
⑴物体向右运动10s的过程中,拉力F对它做多少功?
⑵10s的过程中,拉力F对物体做功的功率是多大?
【答案】W=1600J P= 160W
功率一般表达式:
P = F v cosα
平均功率与瞬时功率
1.平均功率:描述一段时间内物体做功的平均快慢。
2.瞬时功率:表示在某一时刻物体做功的快慢。
讨论:
表示的是平均功率还是瞬时功率?
t表示一段时间时,用公式 求平均功率。
当很短很短时, 表示瞬时功率。
讨论:
表示的是平均功率还是瞬时功率?
瞬时功率: (v是瞬时速度)
平均功率: (v是平均速度)
3、求平均功率
比较常用
(v是平均速度)
求瞬时功率
(v是瞬时速度)
额定功率与实际功率
1.额定功率:是指机器正常工作时的最大输出功率。
2.实际功率:是指机器在工作中实际输出的功率。
机器不一定在额定功率下工作,机器正常工作时实际功率总是小于或等于额定功率,机器只能在短暂时间内实际功率略大于额定功率,但不允许长时间超过额定功率。
在日常生活中,我们经常说某台机器的功率(或某物体做功的功率),实际上是指某个力对物体做功的功率。
思考:
汽车的功率指哪个力做功功率?
汽车牵引力的功率。
起重机吊起货物的功率呢?
钢绳拉力的功率。
五、机车启动问题
当F= f 时,
a=0 ,v达到
最大
保持
vm
匀速
v
F =
v
P
a =
m
F - f
↑
→
↓
↑
→
→
↓
↓
vm=
f
P
(1)、受力分析:
1.方式一:以恒定功率启动
(2)、起动过程分析:(启动过程中阻力不变)
a减小的加速运动
(3)、起动过程描述:
文字描述:
图象描述:
汽车先做加速度逐渐减小的变加速直线运动,
最终以速度 做匀速直线运动。
注意:发动机的功率指牵引力的功率而不是指合外力或阻力的功率。
c、汽车启动过程中加速度与瞬时速度间的对应关系:
(4)、起动过程中的常见问题:
a、汽车启动过程结束即达到最大速度的条件:
b、汽车启动后所能获得的最大速度:
汽车发动机的额定功率为60kW,汽车的质量为5t,汽车在水平路面上行驶时,阻力是车重的0.1倍,g=10m/s2。汽车保持额定功率不变从静止启动后:
①汽车所能达到的最大速度是多大?
②当汽车的加速度为2m/s2时速度多大?
③当汽车的速度为6m/s时加速度多大?
例题1:
12m/s
4m/s
1m/s2
2.方式二:以恒定牵引力起动
(1)、受力分析:
(2)、起动过程分析:(启动过程中阻力不变)
v
↑
P =F v
↑
↑
→
F= f 时,a=0 ,v达到最大
保持 vm匀速运动
F =
v
P额
a =
m
F- f
v
↑
↓
↑
→
↓
→
→
↓
vm=
f
P额
继续加速,匀加速运动过程结束
当P= P额时, P不再改变
→
→
(3)、起动过程描述:
文字描述:
图象描述:
v
t
0
vm
汽车先做匀加速直线运动,再做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
v
3、两种起动方式的比较:
(1)不同点:
以恒定功率起动只有一个变加速阶段,起动过程短,但容易损坏发动机;
以恒定牵引力起动有两个加速阶段,起动过程长,但起动平稳有利于保护发动机。
(2)相同点:
汽车所能达到的最大速度的条件相同,都是当a=0的时候。
1、静摩擦力是不是一定不做功?如果可以做功,一定做负功吗?举例说明以上问题:
F
A
B
静摩擦力可以做正功、做负功,也可以不做功。
静摩擦力对A做负功:W=-f·S
静摩擦力对B做正功:W=f·S
一对静摩擦力做功之和必定为零。
A和B相对静止,一起加速运动。
2、滑动摩擦力是不是一定做功?可以做正功?负功?
v0
滑动摩擦力对滑块做负功
滑动摩擦力对桌子不做功
v0
m
M
SM
Sm
M
v0
m
滑动摩擦力f对物块做负功:
滑动摩擦力f对小车做正功:
一对滑动摩擦力的总功:
滑动摩擦力即可以做正功,也可以做负功,还可以不做功。一对滑动摩擦力对物体作功之和必定为负功。
3、作用力和反作用力做功一定是大小相等,正负相反吗
S
N
S
N
作用力和反作用力,可以做正功,可以做负功,也可以一个力做功另一个力不做功。
S
N
S
N
S
N
质量为5t的汽车,额定功率为P = 90kW,设汽车运动时阻力恒为车重的 0.05 倍。( g = 10 m/s2 )
(1) 求汽车沿水平道路行驶的最大速度;
(2) 设汽车由静止起沿水平道路做匀加速直线运动,加速度 a = 0.4 m/s2,求汽车维持这一加速度行驶的最长时间。
例题2:
解:(1) m = 5000 kg
P = 9.0×104 W
f = kmg = 0.05×5000×10
= 2.5×103 N
P = f vm
vm = P/ f = 9.0×104 / (2.5×103 ) m/s = 36 m/s
v
t
v1
a
t2
vm
t1
O
(2) 汽车做匀加速直线运动完毕时,功率达到最大输出功率,有:
F = f + ma = 4.5×103 N
v = P/F = 9.0×104 /(4.5×103 ) m/s = 20 m/s
t = v/a = 50 s
4、两种起动方式的图像:
(1)以恒定功率启动:
t
0
P
0
t
F
0
t
a
t
v
0
(2)以恒定牵引力启动:
P
t
0
F
t
0
a
t
0
v
t
0
一列火车总质量m=500 t,发动机的额定功率P=6×105W,在水平轨道上行驶时,轨道对火车的阻力f是车重的0.01倍,g取10 m/s2。(1)求火车在水平轨道上行驶的最大速度vm;(2)在水平轨道上,发动机以额定功率P工作,当行驶速度为v1=1 m/s时,求火车的瞬时加速度a1;(3)在水平轨道上以36 km/h的速度匀速行驶时,求发动机的实际功率P′;
【答案】:(1)12 m/s(2)1.1 m/s2(3)5×105 W
质量为m的汽车,启动后沿平直路面行驶,如果发动机的功率恒为P,且行驶过程中受到的摩擦阻力大小一定,汽车速度能够达到的最大值为v,那么当汽车的车速为v/4时,汽车的瞬时加速度的大小为( ) A.P/mv B.2p/mv C.3P/mv D.4P/mv
C
把动力装置分散安装在每节车厢上,使其既具有牵引动力,又可以载客,这样的客车车辆叫做动车.几节自带动力的车辆(动车)加几节不带动力的车辆(也叫拖车)编成一组,就是动车组,假设动车组运行过程中受到的阻力与其所受重力成正比,每节动车与拖车的质量都相等,每节动车的额定功率都相等.若1节动车加3节拖车编成的动车组的最大速度为120 km/h;则6节动车加3节拖车编成的动车组的最大速度为( ). A.120 km/h B.240 km/h C.320 km/h D.480 km/h
C
如图甲所示,在水平路段AB上有一质量为2×103 kg的汽车,正以10m/s的速度向右匀速运动,汽车前方的水平路段BC较粗糙,汽车通过整个ABC路段的v-t图象如图乙所示(在t=15 s处水平虚线与曲线相切),运动过程中汽车发动机的输出功率保持20kW不变,假设汽车在两个路段上受到的阻力(含地面摩擦力和空气阻力等)各自有恒定的大小.
(1)求汽车在AB路段上运动时所受的阻力Ff1;(2)求汽车刚好到达B点时的加速度a;
2 000 N
-1 m/s2
8.1
功与功率
詹姆斯·普雷斯科特·焦耳
詹姆斯·普雷斯科特·焦耳(1818年12月24日-1889年10月11日),英国物理学家,出生于曼彻斯特近郊的沙弗特,由于他在热学、热力学和电方面的贡献,皇家学会授予他最高荣誉的科普利奖章。后人为了纪念他,把能量或功的单位命名为“焦耳”,简称“焦”;并用焦耳姓氏的第一个字母“J”来标记。
重力势能增大
动能增大
弹性势能增大
如果物体在力的作用下能量发生了变化,则这个力一定对物体做了功。
思考:只要有力作用在物体上,这个力就会对物体做功吗
纹丝不动!!
搬不起來超重的金砖
匀速前进
思考:有力,物体也发生了位移,力会对物体做功吗?
参赛者拉着庞大的飞机缓慢前进
归纳:做功的两个必要条件 缺一不可 !
W=F·l
如何计算功?
W=Flcosθ
F1
F2
∵
W1= F1 l = F cosθ l
W2 = 0
W = W1 + W2
∴
一、功
1、概念:物体在力的作用下沿力的方向发生一段位移,则该
力对物体做功。
2、做功条件:①力;②力的方向上的位移
4、单位:
N·m
国际单位:焦耳(J)
1J=1N·m
1J等于1N的力使物体在力的方向上发生1m的位移时所做的功。
5、注意:
(1)公式只适用于恒力做功。即力的大小和方
向恒定且受力物体沿着确定直线运动。
(2)功是标量,只有大小,没有方向,但是有正负。
3、公式:
1. 0 ≤ <90 cos >0 做正功
2. 90 < ≤180 cos <0 做负功
F
F
l
F
l
F
二、功的正负
功的公式:W=Flcosα
α COSα W 物理意义
α=π/2
0≤α<π/2
π/2<α≤π
COSα= 0
COSα>0
COSα<0
W = 0
W > 0
W<0
表示力F对物体不做功
表示力F对物体做正功
表示力F对物体做负功
正负功的物理意义:
动力学角度 能量角度
正功 力的效果是促进物 体的运动,是动力 功是描述力在空间位移
上积累效果的物理量,
是过程量。功的正负既
不描述方向也不描述大
小。做功的过程就是能
量转化的过程。
负功 力的效果是阻碍物 体的运动,是阻力
(1)、分别求出每个力所做的功,然后求出所有功的代数和。
即:W总=W1+W2+……+Wn
(2)、先求出物体所受的合力,然后再求出合力的功,
即:W总=F合Lcosα
求力对物体所做的总功有两种方法:
三、总功
一个质量m=150kg的雪橇,受到与水平方向成θ=37°角斜向上方的拉力F=500N,在水平地面上移动的距离L=5m。物体与地面间的滑动摩擦力F阻=100N。求外力对物体所做的总功。
mg
法1:解:对物体受力分析如图所示,建立沿位移方向的坐标系,把力F分解,因此,合外力的总功为
W=(Fcosθ-f )L
=(500×0.8-100)×5J
=1500J
θ
F
f
mg
FN
解析:拉力F对物体所做的功为
W1= Flcos37°=2000J。
摩擦力F阻对物体所做的功为
W2= F阻lcos180°= -500J。
外力对物体所做的总功
W=W1+W2=1500J。
四、功率
1.定义:一个力所做的功与完成这些功所用时间的比值。
2.公式:
3.物理意义:功率是表示物体做功快慢的物理量。
4.单位:
J/s
瓦特(w)
1w=1J/s=1N·m/s
常用单位——千瓦(kw) 1kw=103w
1马力=735w
5.标矢性:功率是标量。
长时间运动时人的功率为数十瓦,优秀运动员可达1kW
长时间运动马的功率为数百瓦
鱼游动时功率可达350kW
小汽车的功率为数十千瓦至两百千瓦
高速列车的功率可达数万kW
万吨豪华游轮的功率可达数万kW
生活中的功率:
例:一个物体在水平恒力F的作用下,以速度v匀速直线运动了一段时间t,在这段时间t内F做功的功率多大
S
例:如图所示,位于水平面上的物体A,在斜向上的恒定拉力作用下,正以v=2m/s的速度向右做匀速直线运动。已知F的大小为100N,方向与速度v的夹角为37°,求:
⑴物体向右运动10s的过程中,拉力F对它做多少功?
⑵10s的过程中,拉力F对物体做功的功率是多大?
【答案】W=1600J P= 160W
功率一般表达式:
P = F v cosα
平均功率与瞬时功率
1.平均功率:描述一段时间内物体做功的平均快慢。
2.瞬时功率:表示在某一时刻物体做功的快慢。
讨论:
表示的是平均功率还是瞬时功率?
t表示一段时间时,用公式 求平均功率。
当很短很短时, 表示瞬时功率。
讨论:
表示的是平均功率还是瞬时功率?
瞬时功率: (v是瞬时速度)
平均功率: (v是平均速度)
3、求平均功率
比较常用
(v是平均速度)
求瞬时功率
(v是瞬时速度)
额定功率与实际功率
1.额定功率:是指机器正常工作时的最大输出功率。
2.实际功率:是指机器在工作中实际输出的功率。
机器不一定在额定功率下工作,机器正常工作时实际功率总是小于或等于额定功率,机器只能在短暂时间内实际功率略大于额定功率,但不允许长时间超过额定功率。
在日常生活中,我们经常说某台机器的功率(或某物体做功的功率),实际上是指某个力对物体做功的功率。
思考:
汽车的功率指哪个力做功功率?
汽车牵引力的功率。
起重机吊起货物的功率呢?
钢绳拉力的功率。
五、机车启动问题
当F= f 时,
a=0 ,v达到
最大
保持
vm
匀速
v
F =
v
P
a =
m
F - f
↑
→
↓
↑
→
→
↓
↓
vm=
f
P
(1)、受力分析:
1.方式一:以恒定功率启动
(2)、起动过程分析:(启动过程中阻力不变)
a减小的加速运动
(3)、起动过程描述:
文字描述:
图象描述:
汽车先做加速度逐渐减小的变加速直线运动,
最终以速度 做匀速直线运动。
注意:发动机的功率指牵引力的功率而不是指合外力或阻力的功率。
c、汽车启动过程中加速度与瞬时速度间的对应关系:
(4)、起动过程中的常见问题:
a、汽车启动过程结束即达到最大速度的条件:
b、汽车启动后所能获得的最大速度:
汽车发动机的额定功率为60kW,汽车的质量为5t,汽车在水平路面上行驶时,阻力是车重的0.1倍,g=10m/s2。汽车保持额定功率不变从静止启动后:
①汽车所能达到的最大速度是多大?
②当汽车的加速度为2m/s2时速度多大?
③当汽车的速度为6m/s时加速度多大?
例题1:
12m/s
4m/s
1m/s2
2.方式二:以恒定牵引力起动
(1)、受力分析:
(2)、起动过程分析:(启动过程中阻力不变)
v
↑
P =F v
↑
↑
→
F= f 时,a=0 ,v达到最大
保持 vm匀速运动
F =
v
P额
a =
m
F- f
v
↑
↓
↑
→
↓
→
→
↓
vm=
f
P额
继续加速,匀加速运动过程结束
当P= P额时, P不再改变
→
→
(3)、起动过程描述:
文字描述:
图象描述:
v
t
0
vm
汽车先做匀加速直线运动,再做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
v
3、两种起动方式的比较:
(1)不同点:
以恒定功率起动只有一个变加速阶段,起动过程短,但容易损坏发动机;
以恒定牵引力起动有两个加速阶段,起动过程长,但起动平稳有利于保护发动机。
(2)相同点:
汽车所能达到的最大速度的条件相同,都是当a=0的时候。
1、静摩擦力是不是一定不做功?如果可以做功,一定做负功吗?举例说明以上问题:
F
A
B
静摩擦力可以做正功、做负功,也可以不做功。
静摩擦力对A做负功:W=-f·S
静摩擦力对B做正功:W=f·S
一对静摩擦力做功之和必定为零。
A和B相对静止,一起加速运动。
2、滑动摩擦力是不是一定做功?可以做正功?负功?
v0
滑动摩擦力对滑块做负功
滑动摩擦力对桌子不做功
v0
m
M
SM
Sm
M
v0
m
滑动摩擦力f对物块做负功:
滑动摩擦力f对小车做正功:
一对滑动摩擦力的总功:
滑动摩擦力即可以做正功,也可以做负功,还可以不做功。一对滑动摩擦力对物体作功之和必定为负功。
3、作用力和反作用力做功一定是大小相等,正负相反吗
S
N
S
N
作用力和反作用力,可以做正功,可以做负功,也可以一个力做功另一个力不做功。
S
N
S
N
S
N
质量为5t的汽车,额定功率为P = 90kW,设汽车运动时阻力恒为车重的 0.05 倍。( g = 10 m/s2 )
(1) 求汽车沿水平道路行驶的最大速度;
(2) 设汽车由静止起沿水平道路做匀加速直线运动,加速度 a = 0.4 m/s2,求汽车维持这一加速度行驶的最长时间。
例题2:
解:(1) m = 5000 kg
P = 9.0×104 W
f = kmg = 0.05×5000×10
= 2.5×103 N
P = f vm
vm = P/ f = 9.0×104 / (2.5×103 ) m/s = 36 m/s
v
t
v1
a
t2
vm
t1
O
(2) 汽车做匀加速直线运动完毕时,功率达到最大输出功率,有:
F = f + ma = 4.5×103 N
v = P/F = 9.0×104 /(4.5×103 ) m/s = 20 m/s
t = v/a = 50 s
4、两种起动方式的图像:
(1)以恒定功率启动:
t
0
P
0
t
F
0
t
a
t
v
0
(2)以恒定牵引力启动:
P
t
0
F
t
0
a
t
0
v
t
0
一列火车总质量m=500 t,发动机的额定功率P=6×105W,在水平轨道上行驶时,轨道对火车的阻力f是车重的0.01倍,g取10 m/s2。(1)求火车在水平轨道上行驶的最大速度vm;(2)在水平轨道上,发动机以额定功率P工作,当行驶速度为v1=1 m/s时,求火车的瞬时加速度a1;(3)在水平轨道上以36 km/h的速度匀速行驶时,求发动机的实际功率P′;
【答案】:(1)12 m/s(2)1.1 m/s2(3)5×105 W
质量为m的汽车,启动后沿平直路面行驶,如果发动机的功率恒为P,且行驶过程中受到的摩擦阻力大小一定,汽车速度能够达到的最大值为v,那么当汽车的车速为v/4时,汽车的瞬时加速度的大小为( ) A.P/mv B.2p/mv C.3P/mv D.4P/mv
C
把动力装置分散安装在每节车厢上,使其既具有牵引动力,又可以载客,这样的客车车辆叫做动车.几节自带动力的车辆(动车)加几节不带动力的车辆(也叫拖车)编成一组,就是动车组,假设动车组运行过程中受到的阻力与其所受重力成正比,每节动车与拖车的质量都相等,每节动车的额定功率都相等.若1节动车加3节拖车编成的动车组的最大速度为120 km/h;则6节动车加3节拖车编成的动车组的最大速度为( ). A.120 km/h B.240 km/h C.320 km/h D.480 km/h
C
如图甲所示,在水平路段AB上有一质量为2×103 kg的汽车,正以10m/s的速度向右匀速运动,汽车前方的水平路段BC较粗糙,汽车通过整个ABC路段的v-t图象如图乙所示(在t=15 s处水平虚线与曲线相切),运动过程中汽车发动机的输出功率保持20kW不变,假设汽车在两个路段上受到的阻力(含地面摩擦力和空气阻力等)各自有恒定的大小.
(1)求汽车在AB路段上运动时所受的阻力Ff1;(2)求汽车刚好到达B点时的加速度a;
2 000 N
-1 m/s2
