8.2 重力势能 课件-2022-2023学年高一下学期物理人教版(2019)必修第二册(共22张PPT)
文档属性
| 名称 | 8.2 重力势能 课件-2022-2023学年高一下学期物理人教版(2019)必修第二册(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-20 21:51:45 | ||
图片预览







文档简介
(共22张PPT)
8.2
重力势能
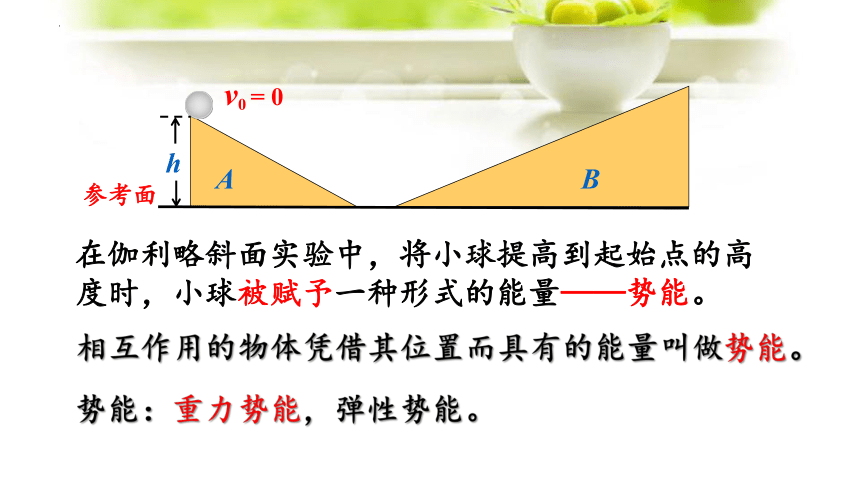
在伽利略斜面实验中,将小球提高到起始点的高度时,小球被赋予一种形式的能量——势能。
相互作用的物体凭借其位置而具有的能量叫做势能。
A
B
h
v0 = 0
参考面
势能:重力势能,弹性势能。
陨石划过天空,放出耀眼的光芒,在地上留下巨大的陨石坑
重力势能:物体由于被举高而使物体具有的能量叫作重力势能。
结论:物体的质量越大、所处的高度越高物体的重力势能就越大!
1)同一课本从不同高度下落到自己手上,感觉
2)不同质量的课本从同一高度下落到自己手上,感觉
用自己的课本做如下试验:
一、重力做功
θ
L
h1
h2
Δh
……
△h1
△h2
△h3
△h4
A
A
A
B
B
B
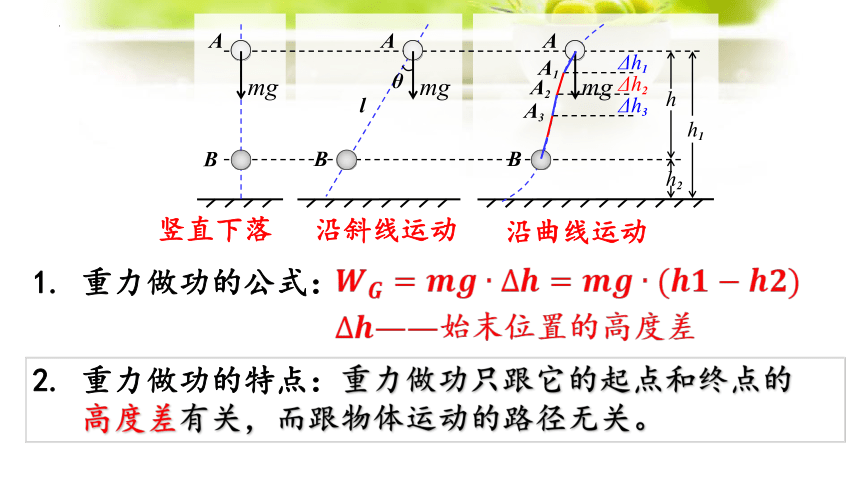
竖直下落
沿斜线运动
沿曲线运动
W1=mgΔh
=mg(h1-h2)
=mgh1-mgh2
W2=mgLcosθ
=mgΔh
=mg(h1-h2)
=mgh1-mgh2
微元法
W3=
B
B
Δh1
Δh2
Δh3
h
h1
h2
A
mg
A1
A2
A3
l
B
θ
mg
A
A
mg
竖直下落
沿斜线运动
沿曲线运动
1. 重力做功的公式:
始末位置的高度差
2. 重力做功的特点:重力做功只跟它的起点和终点的
高度差有关,而跟物体运动的路径无关。
二、重力势能
“mgh”是一个有特殊意义的物理量,一方面与重力做功有关,又随着高度的变化而变化。
1.定义:物体由于被举高而具有的能量,物体的重力
势能等于它所受的重力与所处高度的乘积。
2.定义式:
——相对于重力势能为0的参考
平面的高度。习惯上选择地
面为参考面。
3.单位:焦耳(焦)J
4.标量,状态量。
6.理解:
(1)系统性:重力势能是地球与物体组成的系统所共
有的,而不是地球上的物体单独具有的。
5.重力势能的变化量(增量): ΔEP = mgh2-mgh1
(2)相对性:重力势能的大小与参考面的选取有关,重
力势能有正有负。
(3)任意性:参考面的选取是任意的。
(4)绝对性:重力势能的变化是绝对的,与参考平面
的选择,物体的运动状态无关。
h
h
h
A
h
h
h
A
h
h
h
A
B
B
B
EPB= -3mgh
EPA=2mgh
EPB= -2mgh
EPA=0
EPA=-mgh
EPB=0
重力势能具有相对性,处在参考平面的物体的重力势能为0,参考平面上方的物体的重力势能是正数,参考平面下方物体的重力势能是负数,为了比较势能的大小,应选同一个参考平面。
重力势能的增量△Ep= EPB-EPA =-2mgh
质量为m物体竖直下落从A到B:
A
h
B
h1
h2
三、重力做功与重力势能变化量
参考面
重力做的功
初态的重力势能
末态的重力势能
1.结论:重力所做的功,等于重力势能的减少量。与物
体的运动状态无关,与是否受其它力的作用也
无关。重力所做的功是重力势能改变的唯一量
度。
2.分析:若,重力做正功(重心下移)
,重力势能减小;
若,重力做负功(重心上移)
,重力势能增大;
参考 平面 小球在A点重力势能EpA 小球在B点重力势能EpB A→B下落过程小球重力做功 WG A→B下落过程小球重力势能变化ΔEp
桌面
地面
24J
h1
h2
A
B
-16J
40J
减少40J
40J
0J
40J
减少40J
1.如图有一个质量2kg的小球从桌面以上高h1=1.2m的A点落到地面上的B点,桌面的高h2=0.8m。填写下表(g=10m/s2)。
重力做功与路径无关
2.一质量为5kg的小球从5m高处下落, 碰撞地面后弹起, 每次弹起的高度比下落高度低1m, 求:小球从下落到停在地面的过程中重力一共做了多少功 (g=9.8m/s2)
解:
小球下落高度为5m
=5 x 9.8 x 5J=245J
9
四、弹性势能
1.发生弹性形变的物体的各部分之间,由于有弹力的相互作用,而具有势能,这种势能叫做弹性势能。
弹簧的弹性势能可能与哪些物理量有关?
与弹簧的形变量有关
与弹簧的劲度系数有关
2.弹簧的弹性形变量越大,弹性势能越大。
弹簧的劲度系数(硬度)越大,弹性势能越大。
四、弹性势能
Δl1
…
Δl2
Δln
F=F弹= k l
l
W1 = F1 Δl1
W2 = F2 Δl2
W3 = F3 Δl3
……
W = W1 + W2 + W3 + ……
F 是恒力吗?怎样计算 F 做的功?
F
这个式子怎样求和?
v0
v
O
t
t
v4
t1
t2
t3
t4
v3
v2
v1
v0
v
O
t
t
v0
v
O
t
t
v0
v
O
t
t
v0
v
O
t
t
联想:匀变速直线运动的位移与速度的关系
F拉
l
F拉
O
l
l
Δl1
Δl2
Δl3
Δl5
Δl4
F2
F3
F4
F5
F1
拉力所做的功等于图线与横轴所围的面积!
F拉 = kl
对应:拉力做功与弹簧伸长的关系
F拉
l
(1) l 为弹簧的伸长量或压缩量, k 为弹簧的劲度系数;
(2) 一般规定弹簧在原长时,弹簧的弹性势能为零;
(3) 弹形势能具有相对性,一般相对弹簧原长时的弹性势能;
(4) 弹形势能具有系统性。
四、弹性势能
弹簧弹力做正功,弹性势能减少
弹簧弹力做负功,弹性势能增加
O
A
B
O 点为弹簧的原长
弹簧弹力做正功,弹性势能减少
弹簧弹力做正功,弹性势能减少
弹簧弹力做负功,弹性势能增加
弹簧弹力做负功,弹性势能增加
O
B
O
A
A
O
B
O
四、弹性势能
弹性势能与重力势能的异同
弹性势能 重力势能
定义 发生弹性形变的物体各部分之间由于弹力的相互作用而具有的势能 物体由于被举高而具有的能量。一方面与重力做功相关,另一方面随高度变化而变化,因而叫做物体的重力势能
相对性 弹性势能与零势能位置选取有关,通常选自然长度时,势能为零 重力势能的大小与零势能面的选取有关,但变化量与参考面的选取无关
系统性 弹性势能是弹簧本身具有的能量 重力势能是物体与地球这一系统所共有的
与力做 功的关系 弹性势能的变化等于克服弹力所做的功 重力势能的变化等于克服重力所做的功
8.2
重力势能
在伽利略斜面实验中,将小球提高到起始点的高度时,小球被赋予一种形式的能量——势能。
相互作用的物体凭借其位置而具有的能量叫做势能。
A
B
h
v0 = 0
参考面
势能:重力势能,弹性势能。
陨石划过天空,放出耀眼的光芒,在地上留下巨大的陨石坑
重力势能:物体由于被举高而使物体具有的能量叫作重力势能。
结论:物体的质量越大、所处的高度越高物体的重力势能就越大!
1)同一课本从不同高度下落到自己手上,感觉
2)不同质量的课本从同一高度下落到自己手上,感觉
用自己的课本做如下试验:
一、重力做功
θ
L
h1
h2
Δh
……
△h1
△h2
△h3
△h4
A
A
A
B
B
B
竖直下落
沿斜线运动
沿曲线运动
W1=mgΔh
=mg(h1-h2)
=mgh1-mgh2
W2=mgLcosθ
=mgΔh
=mg(h1-h2)
=mgh1-mgh2
微元法
W3=
B
B
Δh1
Δh2
Δh3
h
h1
h2
A
mg
A1
A2
A3
l
B
θ
mg
A
A
mg
竖直下落
沿斜线运动
沿曲线运动
1. 重力做功的公式:
始末位置的高度差
2. 重力做功的特点:重力做功只跟它的起点和终点的
高度差有关,而跟物体运动的路径无关。
二、重力势能
“mgh”是一个有特殊意义的物理量,一方面与重力做功有关,又随着高度的变化而变化。
1.定义:物体由于被举高而具有的能量,物体的重力
势能等于它所受的重力与所处高度的乘积。
2.定义式:
——相对于重力势能为0的参考
平面的高度。习惯上选择地
面为参考面。
3.单位:焦耳(焦)J
4.标量,状态量。
6.理解:
(1)系统性:重力势能是地球与物体组成的系统所共
有的,而不是地球上的物体单独具有的。
5.重力势能的变化量(增量): ΔEP = mgh2-mgh1
(2)相对性:重力势能的大小与参考面的选取有关,重
力势能有正有负。
(3)任意性:参考面的选取是任意的。
(4)绝对性:重力势能的变化是绝对的,与参考平面
的选择,物体的运动状态无关。
h
h
h
A
h
h
h
A
h
h
h
A
B
B
B
EPB= -3mgh
EPA=2mgh
EPB= -2mgh
EPA=0
EPA=-mgh
EPB=0
重力势能具有相对性,处在参考平面的物体的重力势能为0,参考平面上方的物体的重力势能是正数,参考平面下方物体的重力势能是负数,为了比较势能的大小,应选同一个参考平面。
重力势能的增量△Ep= EPB-EPA =-2mgh
质量为m物体竖直下落从A到B:
A
h
B
h1
h2
三、重力做功与重力势能变化量
参考面
重力做的功
初态的重力势能
末态的重力势能
1.结论:重力所做的功,等于重力势能的减少量。与物
体的运动状态无关,与是否受其它力的作用也
无关。重力所做的功是重力势能改变的唯一量
度。
2.分析:若,重力做正功(重心下移)
,重力势能减小;
若,重力做负功(重心上移)
,重力势能增大;
参考 平面 小球在A点重力势能EpA 小球在B点重力势能EpB A→B下落过程小球重力做功 WG A→B下落过程小球重力势能变化ΔEp
桌面
地面
24J
h1
h2
A
B
-16J
40J
减少40J
40J
0J
40J
减少40J
1.如图有一个质量2kg的小球从桌面以上高h1=1.2m的A点落到地面上的B点,桌面的高h2=0.8m。填写下表(g=10m/s2)。
重力做功与路径无关
2.一质量为5kg的小球从5m高处下落, 碰撞地面后弹起, 每次弹起的高度比下落高度低1m, 求:小球从下落到停在地面的过程中重力一共做了多少功 (g=9.8m/s2)
解:
小球下落高度为5m
=5 x 9.8 x 5J=245J
9
四、弹性势能
1.发生弹性形变的物体的各部分之间,由于有弹力的相互作用,而具有势能,这种势能叫做弹性势能。
弹簧的弹性势能可能与哪些物理量有关?
与弹簧的形变量有关
与弹簧的劲度系数有关
2.弹簧的弹性形变量越大,弹性势能越大。
弹簧的劲度系数(硬度)越大,弹性势能越大。
四、弹性势能
Δl1
…
Δl2
Δln
F=F弹= k l
l
W1 = F1 Δl1
W2 = F2 Δl2
W3 = F3 Δl3
……
W = W1 + W2 + W3 + ……
F 是恒力吗?怎样计算 F 做的功?
F
这个式子怎样求和?
v0
v
O
t
t
v4
t1
t2
t3
t4
v3
v2
v1
v0
v
O
t
t
v0
v
O
t
t
v0
v
O
t
t
v0
v
O
t
t
联想:匀变速直线运动的位移与速度的关系
F拉
l
F拉
O
l
l
Δl1
Δl2
Δl3
Δl5
Δl4
F2
F3
F4
F5
F1
拉力所做的功等于图线与横轴所围的面积!
F拉 = kl
对应:拉力做功与弹簧伸长的关系
F拉
l
(1) l 为弹簧的伸长量或压缩量, k 为弹簧的劲度系数;
(2) 一般规定弹簧在原长时,弹簧的弹性势能为零;
(3) 弹形势能具有相对性,一般相对弹簧原长时的弹性势能;
(4) 弹形势能具有系统性。
四、弹性势能
弹簧弹力做正功,弹性势能减少
弹簧弹力做负功,弹性势能增加
O
A
B
O 点为弹簧的原长
弹簧弹力做正功,弹性势能减少
弹簧弹力做正功,弹性势能减少
弹簧弹力做负功,弹性势能增加
弹簧弹力做负功,弹性势能增加
O
B
O
A
A
O
B
O
四、弹性势能
弹性势能与重力势能的异同
弹性势能 重力势能
定义 发生弹性形变的物体各部分之间由于弹力的相互作用而具有的势能 物体由于被举高而具有的能量。一方面与重力做功相关,另一方面随高度变化而变化,因而叫做物体的重力势能
相对性 弹性势能与零势能位置选取有关,通常选自然长度时,势能为零 重力势能的大小与零势能面的选取有关,但变化量与参考面的选取无关
系统性 弹性势能是弹簧本身具有的能量 重力势能是物体与地球这一系统所共有的
与力做 功的关系 弹性势能的变化等于克服弹力所做的功 重力势能的变化等于克服重力所做的功
