数学人教A版(2019)选择性必修第三册6.3.2二项式系数的性质 课件(共27张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.3.2二项式系数的性质 课件(共27张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-21 07:19:52 | ||
图片预览






文档简介
(共27张PPT)
第六章 计数原理
6.3.2 二项式系数的性质
一
二
三
学习目标
理解二项式系数的性质
会用赋值法求展开式系数的和
会用二项式定理及其性质解决有关的简单问题
1.二项式定理
2.二项展开式的通项
3.二项式系数:
复习引入
有很多有趣的性质,而且我们可以从不同角度进行研究。
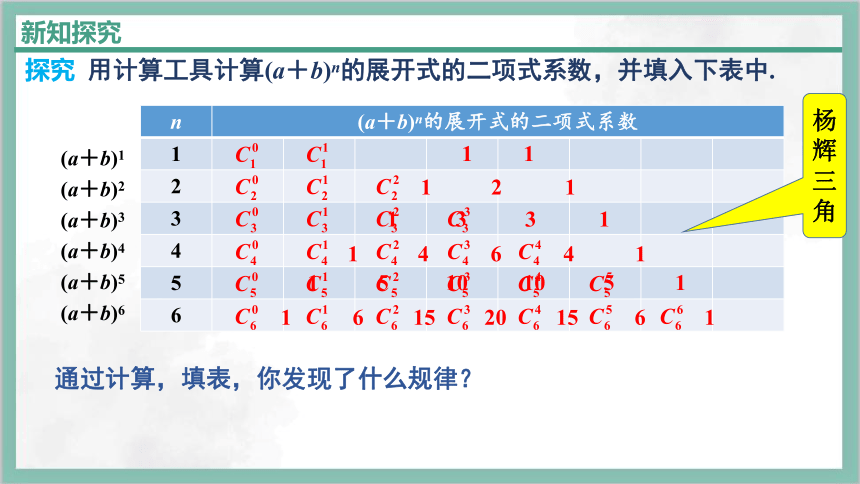
探究 用计算工具计算(a+b)n的展开式的二项式系数,并填入下表中.
n (a+b)n的展开式的二项式系数 1
2
3
4
5
6
通过计算,填表,你发现了什么规律?
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
杨辉三角
新知探究
(1)每行两端的数都是1;
(2)系数呈对称分布;与首末两端“等距离”的两个系数相等;
(3)同一行中,系数先增后减,两端的系数小,中间的系数大.
(4)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和,等等.
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
新知探究
问题1 上表写成如下形式,你发现了什么规律?
对于 展开式的二项式系数:
下面再从函数角度分析二项式系数:
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
新知探究
Cnr可看成是以r为自变量的函数 f (r),其定义域是:
对于确定的n,我们还可以画出
它的图像.
例如,当n=6 时,f (r)=Cnr (r∈
{0, 1, 2, 3, 4, 5, 6})的图象是右图中的7个离散点.
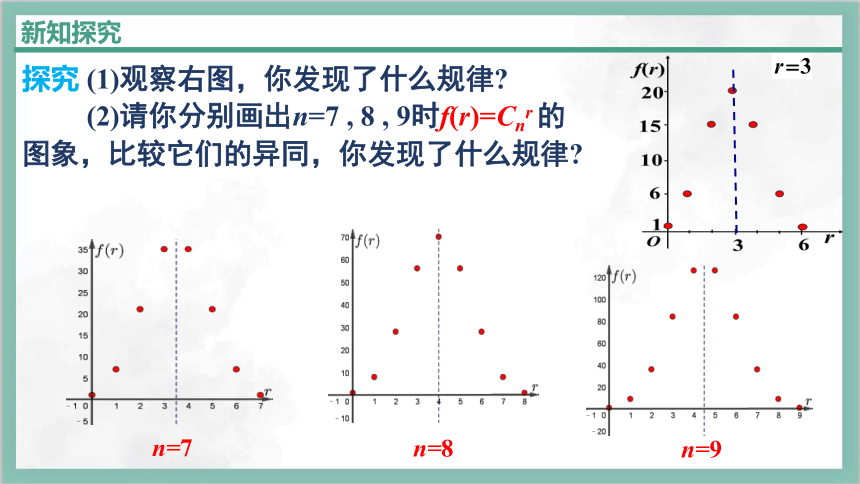
探究 (1)观察右图,你发现了什么规律
(2)请你分别画出n=7 , 8 , 9时f(r)=Cnr 的图象,比较它们的异同,你发现了什么规律
新知探究
n=7
n=8
n=9
与首末两端“等距离”的两个二项式系数相等.
这一性质可直接由公式 得到.
f (r)
r
n
O
5
15
20
1
10
图象的对称轴:
概念生成
由此我们可得二项式系数有以下性质:
性质1:对称性
新知探究
性质2:增减性与最大值
(增减性的实质是比较 的大小)
所以 相对于 的增减情况由 决定.
可知,当 时,
由:
由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值
二项式系数是逐渐增大的,
新知探究
性质2:增减性与最大值
∴(1)当n为偶数时,正中间一项的二项式系数 最大;
(2)当n为奇数时,中间两项的二项式系数 相等,且同时取得最大值.
∵二项展开式共有n+1项,
f (k)
k
n
3
O
5
15
20
1
10
1
2
4
5
n为偶数
f (r)
r
n
O
5
15
20
1
10
n为奇数
性质3: 各二项式系数的和
新知探究
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
=
=
=
=
=
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
2
4
8
16
32
猜想:
问题2 计算各二项式的系数之和,你能发现什么规律?
=21
=22
=23
=24
=25
+
+
+
+
+
+
=
26
求证:(a+b)n 的展开式中的所有二项式系数的和等于 .
证明:
令 a=1, b=1,则得
在展开式 中
性质3: 各二项式系数的和
新知探究
(赋值法)
令x =1,得
另证:
结论:
组合总数公式
一般地, 的展开式的二项式系数有如下性质:
(1)
(2)
(3)当 时,
当 时,
(4)
二项式系数性质
课堂小结
典例解析
例1 证明:在(a+b)n展开式中, 奇数项的二项式系数的和等于偶数项的二项式系数的和.
偶数项的二项式系数的和为
中的a, b可以取任意实数, 因此我们可以通过对a , b适当赋值来得到上述两个系数和.
分析:奇数项的二项式系数的和为
证明:在展开式 中
典例解析
例1 证明:在(a+b)n展开式中, 奇数项的二项式系数的和等于偶数项的二项式系数的和.
令a=1, b= -1,则得
思考
结合二项式系数和为2n
巩固练习
课本34页
解:
巩固练习
课本34页
证明:
1
巩固练习
课本34页
n
1
2
3
4
5
6
7
8
9
10
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 1
1 9 36 84 126 84 36 9 1
1 10 45 120 210 252 120 45 10 1
巩固练习
课本34页
解:
典例解析
例2
赋值法的应用—解决二项式系数问题.
解:
典例解析
赋值法的应用—解决二项式系数问题.
例2
解:
典例解析
赋值法的应用—解决二项式系数问题.
例2
解:
思考:
方法:
典例小结
小结:求奇次项系数之和与偶次项系数的和
可以先赋值,然后解方程组整体求解
证: 要证 成立,
只需证 成立
所以
例3
典例解析
典例解析
例4 用二项式定理证明:
证明
,
能被100整除.
方法总结:利用二项式定理可以解决求余数和整除的问题,通常需将底数化成两数的和或差的形式,且这种转化形式与除数有密切的关系.
例5 (1+2x)3(1-x)4的展开式中,含x项的系数为( )
A.10 B.-10 C.2 D.-2
C
解: (1+2x)3(1-x)4的展开式中含x项的系数是由两个因式相乘而得到的,
即第一个因式的常数项和一次项分别乘第二个因式的一次项与常数项,
典例解析
课堂小结
第六章 计数原理
6.3.2 二项式系数的性质
一
二
三
学习目标
理解二项式系数的性质
会用赋值法求展开式系数的和
会用二项式定理及其性质解决有关的简单问题
1.二项式定理
2.二项展开式的通项
3.二项式系数:
复习引入
有很多有趣的性质,而且我们可以从不同角度进行研究。
探究 用计算工具计算(a+b)n的展开式的二项式系数,并填入下表中.
n (a+b)n的展开式的二项式系数 1
2
3
4
5
6
通过计算,填表,你发现了什么规律?
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
杨辉三角
新知探究
(1)每行两端的数都是1;
(2)系数呈对称分布;与首末两端“等距离”的两个系数相等;
(3)同一行中,系数先增后减,两端的系数小,中间的系数大.
(4)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和,等等.
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
新知探究
问题1 上表写成如下形式,你发现了什么规律?
对于 展开式的二项式系数:
下面再从函数角度分析二项式系数:
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
新知探究
Cnr可看成是以r为自变量的函数 f (r),其定义域是:
对于确定的n,我们还可以画出
它的图像.
例如,当n=6 时,f (r)=Cnr (r∈
{0, 1, 2, 3, 4, 5, 6})的图象是右图中的7个离散点.
探究 (1)观察右图,你发现了什么规律
(2)请你分别画出n=7 , 8 , 9时f(r)=Cnr 的图象,比较它们的异同,你发现了什么规律
新知探究
n=7
n=8
n=9
与首末两端“等距离”的两个二项式系数相等.
这一性质可直接由公式 得到.
f (r)
r
n
O
5
15
20
1
10
图象的对称轴:
概念生成
由此我们可得二项式系数有以下性质:
性质1:对称性
新知探究
性质2:增减性与最大值
(增减性的实质是比较 的大小)
所以 相对于 的增减情况由 决定.
可知,当 时,
由:
由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值
二项式系数是逐渐增大的,
新知探究
性质2:增减性与最大值
∴(1)当n为偶数时,正中间一项的二项式系数 最大;
(2)当n为奇数时,中间两项的二项式系数 相等,且同时取得最大值.
∵二项展开式共有n+1项,
f (k)
k
n
3
O
5
15
20
1
10
1
2
4
5
n为偶数
f (r)
r
n
O
5
15
20
1
10
n为奇数
性质3: 各二项式系数的和
新知探究
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
=
=
=
=
=
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
2
4
8
16
32
猜想:
问题2 计算各二项式的系数之和,你能发现什么规律?
=21
=22
=23
=24
=25
+
+
+
+
+
+
=
26
求证:(a+b)n 的展开式中的所有二项式系数的和等于 .
证明:
令 a=1, b=1,则得
在展开式 中
性质3: 各二项式系数的和
新知探究
(赋值法)
令x =1,得
另证:
结论:
组合总数公式
一般地, 的展开式的二项式系数有如下性质:
(1)
(2)
(3)当 时,
当 时,
(4)
二项式系数性质
课堂小结
典例解析
例1 证明:在(a+b)n展开式中, 奇数项的二项式系数的和等于偶数项的二项式系数的和.
偶数项的二项式系数的和为
中的a, b可以取任意实数, 因此我们可以通过对a , b适当赋值来得到上述两个系数和.
分析:奇数项的二项式系数的和为
证明:在展开式 中
典例解析
例1 证明:在(a+b)n展开式中, 奇数项的二项式系数的和等于偶数项的二项式系数的和.
令a=1, b= -1,则得
思考
结合二项式系数和为2n
巩固练习
课本34页
解:
巩固练习
课本34页
证明:
1
巩固练习
课本34页
n
1
2
3
4
5
6
7
8
9
10
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 1
1 9 36 84 126 84 36 9 1
1 10 45 120 210 252 120 45 10 1
巩固练习
课本34页
解:
典例解析
例2
赋值法的应用—解决二项式系数问题.
解:
典例解析
赋值法的应用—解决二项式系数问题.
例2
解:
典例解析
赋值法的应用—解决二项式系数问题.
例2
解:
思考:
方法:
典例小结
小结:求奇次项系数之和与偶次项系数的和
可以先赋值,然后解方程组整体求解
证: 要证 成立,
只需证 成立
所以
例3
典例解析
典例解析
例4 用二项式定理证明:
证明
,
能被100整除.
方法总结:利用二项式定理可以解决求余数和整除的问题,通常需将底数化成两数的和或差的形式,且这种转化形式与除数有密切的关系.
例5 (1+2x)3(1-x)4的展开式中,含x项的系数为( )
A.10 B.-10 C.2 D.-2
C
解: (1+2x)3(1-x)4的展开式中含x项的系数是由两个因式相乘而得到的,
即第一个因式的常数项和一次项分别乘第二个因式的一次项与常数项,
典例解析
课堂小结
