苏科版数学七年级下册 10.5 用二元一次方程组解决问题(3)教案(表格式)
文档属性
| 名称 | 苏科版数学七年级下册 10.5 用二元一次方程组解决问题(3)教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 26.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 00:00:00 | ||
图片预览

文档简介
课题 10.5 用二元一次方程组解决问题(3)
教学目标 1.能够借助示意图解决复杂问题的的等量关系,体会示意图在分析问题时的化繁为简的特点; 2.能够借助数学模型独立列出二元一次方程组,解决问题; 3.培养学生分析问题,解决问题的能力,感受方程的作用。
教学重难点 借助示意图解决复杂问题的的等量关系,独立列出二元一次方程组。
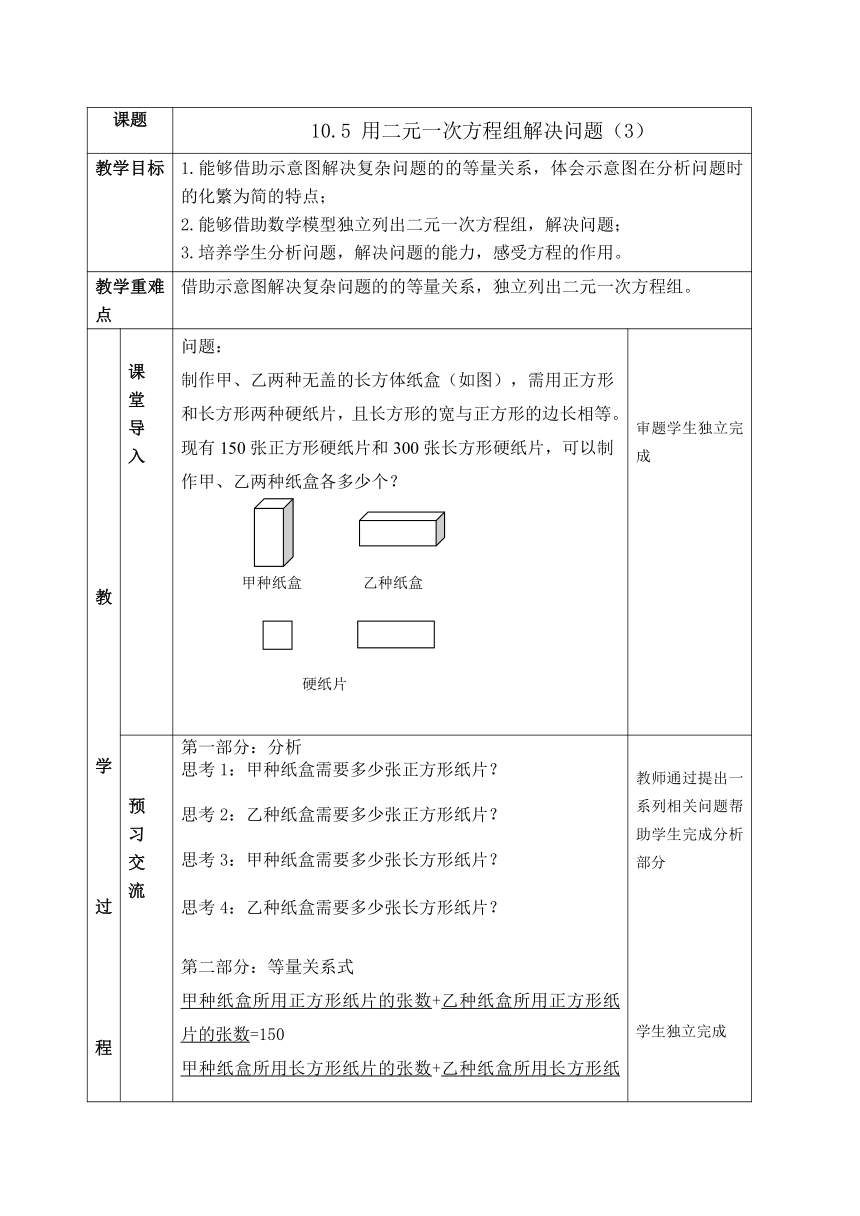
教 学 过 程 课 堂 导 入 问题: 制作甲、乙两种无盖的长方体纸盒(如图),需用正方形和长方形两种硬纸片,且长方形的宽与正方形的边长相等。现有150张正方形硬纸片和300张长方形硬纸片,可以制作甲、乙两种纸盒各多少个? 甲种纸盒 乙种纸盒 硬纸片 审题学生独立完成
预 习 交 流 第一部分:分析 思考1:甲种纸盒需要多少张正方形纸片? 思考2:乙种纸盒需要多少张正方形纸片? 思考3:甲种纸盒需要多少张长方形纸片? 思考4:乙种纸盒需要多少张长方形纸片? 第二部分:等量关系式 甲种纸盒所用正方形纸片的张数+乙种纸盒所用正方形纸片的张数=150 甲种纸盒所用长方形纸片的张数+乙种纸盒所用长方形纸片的张数 =300 第三部分:设未知数,列方程 解:设可制作甲种纸盒x个,乙种纸盒y个 由题意得 解这个方程得 答:可制作甲种纸盒30个,乙种纸盒60个. 教师通过提出一系列相关问题帮助学生完成分析部分 学生独立完成 学生独立完成,学生代表板书
例题讲解 例1:某铁路桥长1000m,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min,整列火车完全在桥上的时间共40s.求火车的速度和长度. 第一部分:分析 思考1:火车从开始上桥到完全过桥走过的路程是多少? 思考2:整列火车完全在桥上时走过的路程是什么? 思考3:示意图如何画? 第二部分:等量关系式 火车的速度×60s=火车从开始上桥到完全过桥走过的路程 火车的速度×40s=整列火车完全在桥上时走过的路程 第三部分:解题 解:设火车的速度为min/s,设火车的长为m. 由题意得 解这个方程得 答:火车的速度为20min/s,设火车的长为200m. 巩固练习 1.某旅馆的客房有三人间和两人间两种,三人间每人每天45元,两人间每人每间70,现有一个40人的旅游团到此旅馆住宿,住了若干间房,且每间房都住满,住宿费是2200元,求两种房间各定了多少间? 2.甲乙两车相距280千米,若相向而行,则2小时相遇;若同向而行,乙14小时追上甲,求甲乙两车的速度。 学生独立完成审题,注意单位的变化 教师帮助学生完成题目分析后,学生独立完成解题过程。 学生独立完成 学生代表分享结果
课堂总结 学会借助示意图分析较复杂的等量关系,简化问题
课后作业 课本111页习题10.5第6、8题;
教学目标 1.能够借助示意图解决复杂问题的的等量关系,体会示意图在分析问题时的化繁为简的特点; 2.能够借助数学模型独立列出二元一次方程组,解决问题; 3.培养学生分析问题,解决问题的能力,感受方程的作用。
教学重难点 借助示意图解决复杂问题的的等量关系,独立列出二元一次方程组。
教 学 过 程 课 堂 导 入 问题: 制作甲、乙两种无盖的长方体纸盒(如图),需用正方形和长方形两种硬纸片,且长方形的宽与正方形的边长相等。现有150张正方形硬纸片和300张长方形硬纸片,可以制作甲、乙两种纸盒各多少个? 甲种纸盒 乙种纸盒 硬纸片 审题学生独立完成
预 习 交 流 第一部分:分析 思考1:甲种纸盒需要多少张正方形纸片? 思考2:乙种纸盒需要多少张正方形纸片? 思考3:甲种纸盒需要多少张长方形纸片? 思考4:乙种纸盒需要多少张长方形纸片? 第二部分:等量关系式 甲种纸盒所用正方形纸片的张数+乙种纸盒所用正方形纸片的张数=150 甲种纸盒所用长方形纸片的张数+乙种纸盒所用长方形纸片的张数 =300 第三部分:设未知数,列方程 解:设可制作甲种纸盒x个,乙种纸盒y个 由题意得 解这个方程得 答:可制作甲种纸盒30个,乙种纸盒60个. 教师通过提出一系列相关问题帮助学生完成分析部分 学生独立完成 学生独立完成,学生代表板书
例题讲解 例1:某铁路桥长1000m,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min,整列火车完全在桥上的时间共40s.求火车的速度和长度. 第一部分:分析 思考1:火车从开始上桥到完全过桥走过的路程是多少? 思考2:整列火车完全在桥上时走过的路程是什么? 思考3:示意图如何画? 第二部分:等量关系式 火车的速度×60s=火车从开始上桥到完全过桥走过的路程 火车的速度×40s=整列火车完全在桥上时走过的路程 第三部分:解题 解:设火车的速度为min/s,设火车的长为m. 由题意得 解这个方程得 答:火车的速度为20min/s,设火车的长为200m. 巩固练习 1.某旅馆的客房有三人间和两人间两种,三人间每人每天45元,两人间每人每间70,现有一个40人的旅游团到此旅馆住宿,住了若干间房,且每间房都住满,住宿费是2200元,求两种房间各定了多少间? 2.甲乙两车相距280千米,若相向而行,则2小时相遇;若同向而行,乙14小时追上甲,求甲乙两车的速度。 学生独立完成审题,注意单位的变化 教师帮助学生完成题目分析后,学生独立完成解题过程。 学生独立完成 学生代表分享结果
课堂总结 学会借助示意图分析较复杂的等量关系,简化问题
课后作业 课本111页习题10.5第6、8题;
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
