苏科版数学九年级下册 6.4 探索三角形相似的条件 课件(共20张PPT)
文档属性
| 名称 | 苏科版数学九年级下册 6.4 探索三角形相似的条件 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 846.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-21 20:50:34 | ||
图片预览

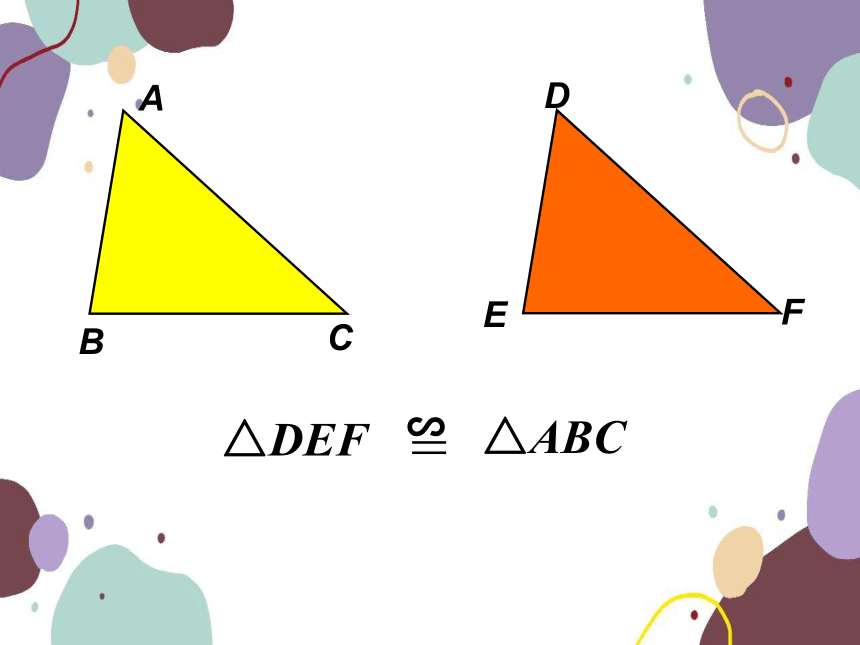

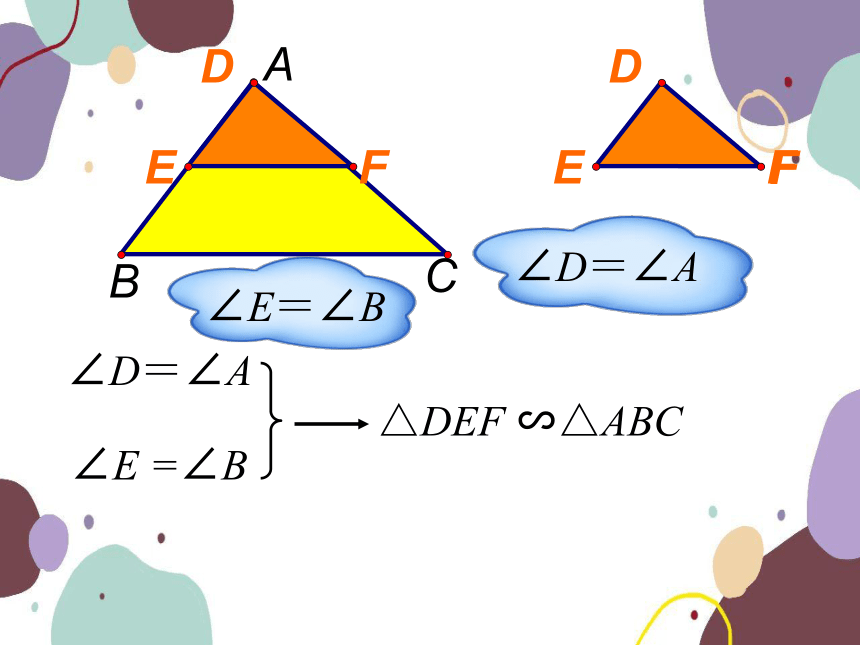


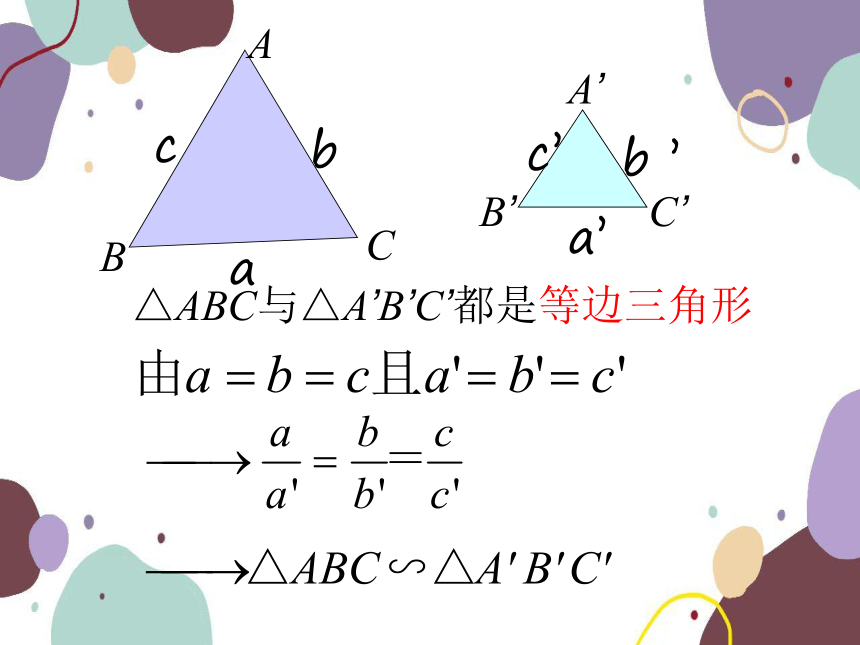
文档简介
(共20张PPT)
6.4 探索三角形相似的条件
=
F
E
D
C
B
A
△DEF
∽
△ABC
全等判定:
(对应)边角都等
(6组量)
判定方法
角边角
角角边
边边边
边角边
三角对应相等, 三边对应成比例
1. 两角对应相等
3. 两边对应成比例 且夹角相等
2. 三边对应成比例
4.两边对应成比例且
其中一边的对角相等
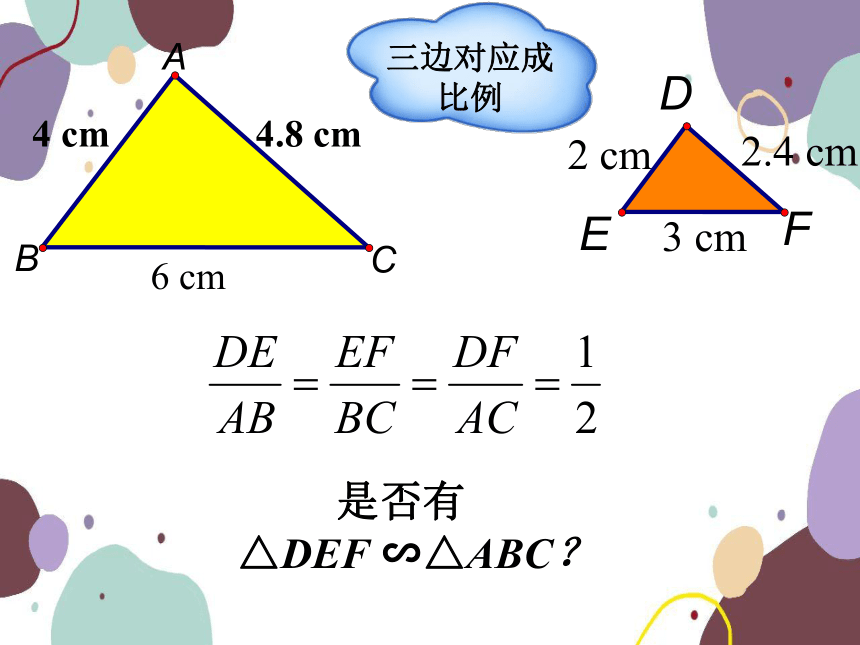
6 cm
4 cm
4.8 cm
3 cm
2.4 cm
2 cm
是否有
△DEF ∽△ABC?
A
B
C
F
E
D
三边对应成 比例
A
B
C
F
E
D
∠E =∠B
△DEF ∽△ABC
F
F
E
D
∠D=∠A
∠D=∠A
∠E=∠B
三条边对应成比例的
两个三角形相似.
△DEF ∽△ABC
6 cm
4 cm
4.8 cm
A
B
C
3 cm
2.4 cm
2 cm
F
E
D
两个等边三角形一定相似吗?
△ABC与△A’B’C’都是等边三角形
A
C
B
c
a
b
A’
B’
C’
c’
a’
b’
是否有
△ABC∽△A’B’C’
A
C
B
c
a
b
A’
B’
C’
c’
a’
b ’
△ABC与△A’B’C’都是等边三角形
A
B
C
C'
B'
A'
6 cm
4 cm
3 cm
2 cm
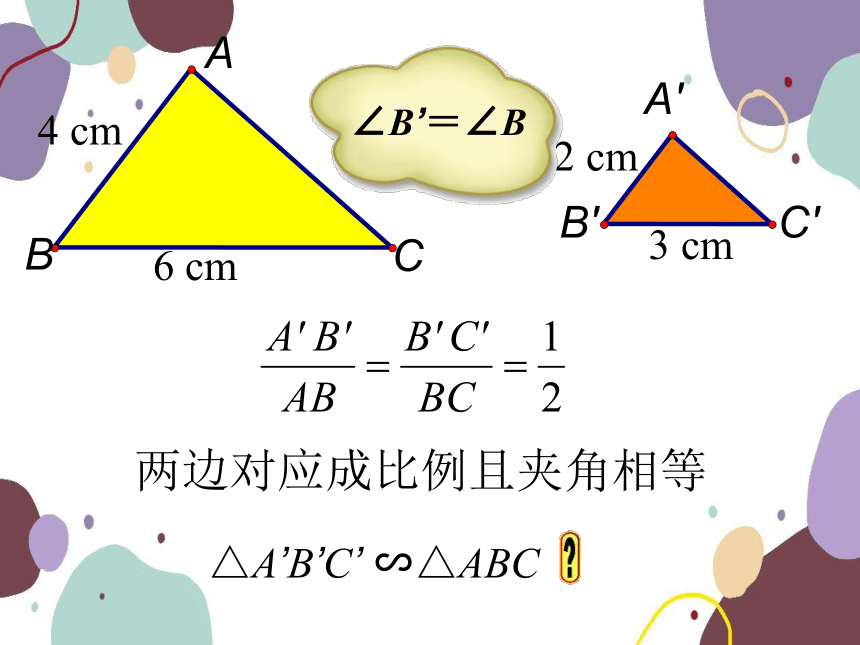
两边对应成比例且夹角相等
△A’B’C’ ∽△ABC
∠B’=∠B
A
B
C
C'
B'
A'
△A’B’C’ ∽△ABC
∠B’=∠B
∠B’=∠B
C'
B'
A'
C'
B'
A'
两边对应成比例且其中一边的对角对应相等的两个三角形是否相似呢?
D
A
B
C
C'
B'
A'
已知:△A’B’C’ ∽△ABC
在△ABC中,以B为圆心,
连结BD,则BD=BA.
BA长为半径画弧,交AC于D,
看已知条件
判定相似
选方法
找够判定方法中所需的条件
想一想
好高的纪念碑呀!相当于几层楼高呢?
他在干吗呢?
想到办法了
走过去, 嗯~~, 一共150步
又是100步~
到底在干吗呢?
我知道了,相当于六层楼高
你能用所学的知识说说这样做的理由吗?
A
B
C
D
F
在某建筑工地上,有 一种钢筋三角架,三边分 别是 20cm,50cm,60cm, 因工程需要,现急需做一 个与其相似的三角形钢筋架,而工地里只有两根长为30cm和50cm的钢筋,再去购买原料又来不及,只能是尽可能的使用现有的原料了,这该怎么办呢?
你能来帮帮他们吗?
解: (1) 当30cm的钢筋作为第二个三角形最长边时,设另两边应为x cm,y cm,则应有: ,所以x=10cm,y=25cm.
(2) 当30cm的钢筋作为第二个三角形中长边时,设另两边应为x cm,y cm,则应有: ,所以x=12cm,y=36cm.
(3) 当30cm的钢筋作为第二个三角形最短边时,设另两边应为x cm,y cm,则应有: ,所以x=75cm,y=90cm.
而x+y>50这不可能,故此情况不会发生.
小结
两个三角形相似的判别方法:
(1) 两角对应相等的两个三角形相似.
(2) 三边对应成比例的两个三角形相似.
(3) 两边对应成比例且夹角相等的两个 三角形相似.
6.4 探索三角形相似的条件
=
F
E
D
C
B
A
△DEF
∽
△ABC
全等判定:
(对应)边角都等
(6组量)
判定方法
角边角
角角边
边边边
边角边
三角对应相等, 三边对应成比例
1. 两角对应相等
3. 两边对应成比例 且夹角相等
2. 三边对应成比例
4.两边对应成比例且
其中一边的对角相等
6 cm
4 cm
4.8 cm
3 cm
2.4 cm
2 cm
是否有
△DEF ∽△ABC?
A
B
C
F
E
D
三边对应成 比例
A
B
C
F
E
D
∠E =∠B
△DEF ∽△ABC
F
F
E
D
∠D=∠A
∠D=∠A
∠E=∠B
三条边对应成比例的
两个三角形相似.
△DEF ∽△ABC
6 cm
4 cm
4.8 cm
A
B
C
3 cm
2.4 cm
2 cm
F
E
D
两个等边三角形一定相似吗?
△ABC与△A’B’C’都是等边三角形
A
C
B
c
a
b
A’
B’
C’
c’
a’
b’
是否有
△ABC∽△A’B’C’
A
C
B
c
a
b
A’
B’
C’
c’
a’
b ’
△ABC与△A’B’C’都是等边三角形
A
B
C
C'
B'
A'
6 cm
4 cm
3 cm
2 cm
两边对应成比例且夹角相等
△A’B’C’ ∽△ABC
∠B’=∠B
A
B
C
C'
B'
A'
△A’B’C’ ∽△ABC
∠B’=∠B
∠B’=∠B
C'
B'
A'
C'
B'
A'
两边对应成比例且其中一边的对角对应相等的两个三角形是否相似呢?
D
A
B
C
C'
B'
A'
已知:△A’B’C’ ∽△ABC
在△ABC中,以B为圆心,
连结BD,则BD=BA.
BA长为半径画弧,交AC于D,
看已知条件
判定相似
选方法
找够判定方法中所需的条件
想一想
好高的纪念碑呀!相当于几层楼高呢?
他在干吗呢?
想到办法了
走过去, 嗯~~, 一共150步
又是100步~
到底在干吗呢?
我知道了,相当于六层楼高
你能用所学的知识说说这样做的理由吗?
A
B
C
D
F
在某建筑工地上,有 一种钢筋三角架,三边分 别是 20cm,50cm,60cm, 因工程需要,现急需做一 个与其相似的三角形钢筋架,而工地里只有两根长为30cm和50cm的钢筋,再去购买原料又来不及,只能是尽可能的使用现有的原料了,这该怎么办呢?
你能来帮帮他们吗?
解: (1) 当30cm的钢筋作为第二个三角形最长边时,设另两边应为x cm,y cm,则应有: ,所以x=10cm,y=25cm.
(2) 当30cm的钢筋作为第二个三角形中长边时,设另两边应为x cm,y cm,则应有: ,所以x=12cm,y=36cm.
(3) 当30cm的钢筋作为第二个三角形最短边时,设另两边应为x cm,y cm,则应有: ,所以x=75cm,y=90cm.
而x+y>50这不可能,故此情况不会发生.
小结
两个三角形相似的判别方法:
(1) 两角对应相等的两个三角形相似.
(2) 三边对应成比例的两个三角形相似.
(3) 两边对应成比例且夹角相等的两个 三角形相似.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
