人教版 五年级下册长方体和正方体表面积说课课件(共24张PPT)
文档属性
| 名称 | 人教版 五年级下册长方体和正方体表面积说课课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 765.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-21 17:00:58 | ||
图片预览








文档简介
(共24张PPT)
一、教材分析
二、教法和学法
三、教学准备
四、教学程序
一、教学分析
(一)说课内容
(二)教材的地位、作用
(四)教学目标
(五)重点、难点
(三)学情分析
二、教法、学法
教法:
设疑诱导法、自组讨论法、操作发现法、直观演示法、练习应用法等。
学法:
动手操作法、观察发现法、自主探究法、
合作交流法等。
三、教学准备
多媒体课件 、 包装纸、
长方体和正方体纸盒、
剪刀 、彩笔 、直尺等
四、教学程序
(一)创设情境,引入新课(2分钟)
(二)自主探究,感悟新知(26分钟)
(三)综合实践,学以致用(12分钟)
(四)课堂小结(5分钟)
(一)创设情境,引入新课
明天是妈妈的生日,我跟妈妈买了一份礼物,可是礼物的盒子不够精美,你们能不能帮我想想办法?
想知道包装纸的大小吗?
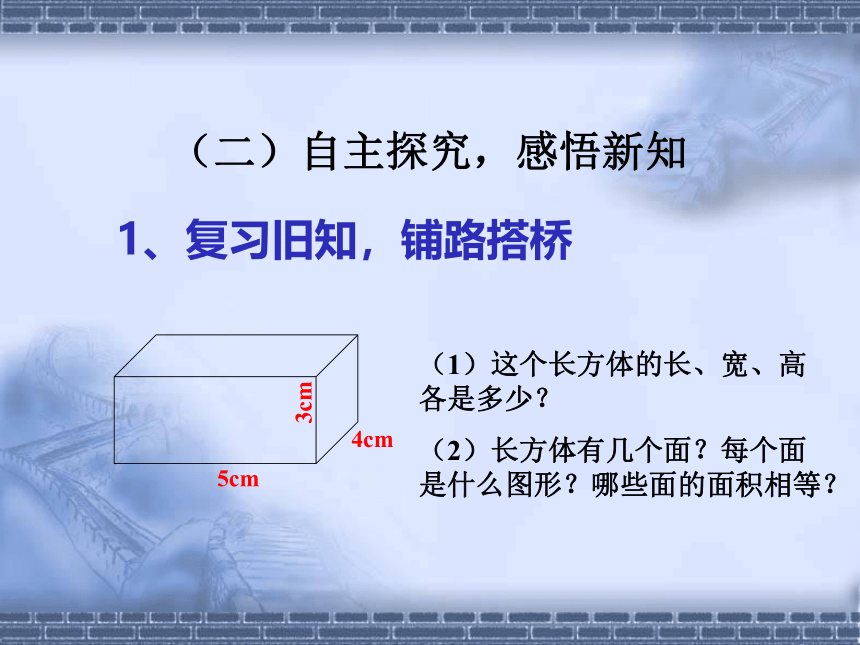
(二)自主探究,感悟新知
1、复习旧知,铺路搭桥
4cm
3cm
5cm
(1)这个长方体的长、宽、高各是多少?
(2)长方体有几个面?每个面是什么图形?哪些面的面积相等?
2、动手操作,合作探究
(2)小组合作,动手操作并交流讨论:
1)长方体、正方体展开是什么样的?
2)拿出准备好的长方体和正方体纸盒沿棱剪开,然后将自己剪开的长方体或正方体纸盒展开,你发现了什么?
(1)摸一摸
拿出一个长方体纸盒,用手摸一摸长方体表面,观察6个面分别是什么形状,并标出“上、下、前、后、左、右”。
3)想一想,长方体和正方体的表面积与这6个面有什么
关系呢?
长方体或正方体6个面的总面积,叫做它的表面积。
3、自主探究,深化主题
上下、左右、前后各个面的长和宽分别是原长方体的什么?
一个长方体剪开的每个面是什么形状?展开后哪两个面是相对的面,有几组相等的面?
下
后
上
前
左
右
观察长方体展开图,分小组带着问题讨论:
前
上下面:长×宽×2
前后面:长×高×2
左右面:高×宽×2
上
下
左
右
后
做一个微波炉的包装箱,至少要用多少平方米的硬纸板
0.7m
0.5m
0.4m
这里要求的是这个长方体包装箱的表面积。
上、下每个面,长_____,宽_____,面积是_______;
前、后每个面,长_____,宽_____,面积是_______;
左、右每个面,长_____,宽_____,面积是_______。
0.7m
0.5m
0.35m2
0.7m
0.4m
0.28m2
0.5m
0.4m
0.2m2
4、教学例1
0.7m
0.5m
0.4m
这个包装箱的表面积是:
0.35×2+0.28×2+0.2×2
=0.7+0.56+0.4
=1.66(m2)
答:至少要用1.66m2硬纸板。
说一说:你是怎么计算的?
解法一:0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
= 0.35×2+0.28×2+0.2×2
=0.7+0.56+0.4
=1.66(m2)
解法二:(0.7×0.5+0.7×0.4+0.5×0.4)×2
=(0.35+0.28+0.2)×2
=0.83×2
= 1.66(m2)
这两种解法有什么不同?有什么联系?
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
长方体的表面积=(长×宽+长×高+宽×高)×2
S=2(a×b+a×h+b×h)
一个正方体墨水盒,棱长6.5cm。制作这个墨水盒至少需要多少平方厘米的硬纸板?
6.5×6.5×6
=42.25×6
=253.5(cm2)
答:制作这个墨水盒至少需要253.5cm2的硬纸板。
求至少用多少平方厘米的硬纸板,就是要求什么 自己试一试!
5、教学例2
正方体表面积=棱长×棱长×6
S=6a2
想一想,正方体表面积的计算方法是什么?
制作右面这样一个长方体纸盒。至少要用多少平方厘米的纸板?
5cm
4cm
8cm
8×5 ×2 +8×4 ×2 +5×4×2
=80+64+40
=184(平方厘米)
答:至少要用184平方厘米的纸板。
(三)综合实践,学以致用
1、基础练习
2、巩固提高
(1) 亮亮家要给一个长0.75m,宽0.5m,高1.6m的简易衣柜换布罩(如下图,没有底面)。至少需要用布多少平方米
0.75m
0.5m
1.6m
(2) 一个玻璃鱼缸的形状是正方体,棱长3dm。制作这个鱼缸时至少需要玻璃多少平方分米 (鱼缸的上面没有盖。)
3×3×5=45(dm2)
答:制作这个鱼缸时至少需要玻璃45dm2。
想一想,在日常生活中,做哪些事与求长方体、正方体的部分面积有关?
3.拓展延伸
小组合作:
测量火柴盒的长、宽、高,并计算做这样一个
火柴盒需要多少纸板?
(四)课堂小结
谈谈你在本节课中收获到了什么?
长方体和正方体的表面积
正方体的表面积=棱长×棱长×6
长方体上面(或下面)的面积=长×宽
长方体前面(或后面)的面积=长×高
长方体左面(或右面)的面积=宽×高
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
或=(长×宽+长×高+高×宽)× 2
长方体或正方体6个面的总面积,叫做它的表面积。
S=2(a×b+a×h+b×h)
S=6a2
(五)教学反思
本节课教学也存在一定的不足,例如,优生在课堂上仍是主角,学困生由于动手能力差,思维跟不上,大部分时间只能充当观众与听众,从课堂练习可以看出他们对所学的知识一知半解,课堂如果让他们充分动手操作与表达,又会花费大量的时间,如何解决这样的矛盾,仍是我今后的重要研究内容。
一、教材分析
二、教法和学法
三、教学准备
四、教学程序
一、教学分析
(一)说课内容
(二)教材的地位、作用
(四)教学目标
(五)重点、难点
(三)学情分析
二、教法、学法
教法:
设疑诱导法、自组讨论法、操作发现法、直观演示法、练习应用法等。
学法:
动手操作法、观察发现法、自主探究法、
合作交流法等。
三、教学准备
多媒体课件 、 包装纸、
长方体和正方体纸盒、
剪刀 、彩笔 、直尺等
四、教学程序
(一)创设情境,引入新课(2分钟)
(二)自主探究,感悟新知(26分钟)
(三)综合实践,学以致用(12分钟)
(四)课堂小结(5分钟)
(一)创设情境,引入新课
明天是妈妈的生日,我跟妈妈买了一份礼物,可是礼物的盒子不够精美,你们能不能帮我想想办法?
想知道包装纸的大小吗?
(二)自主探究,感悟新知
1、复习旧知,铺路搭桥
4cm
3cm
5cm
(1)这个长方体的长、宽、高各是多少?
(2)长方体有几个面?每个面是什么图形?哪些面的面积相等?
2、动手操作,合作探究
(2)小组合作,动手操作并交流讨论:
1)长方体、正方体展开是什么样的?
2)拿出准备好的长方体和正方体纸盒沿棱剪开,然后将自己剪开的长方体或正方体纸盒展开,你发现了什么?
(1)摸一摸
拿出一个长方体纸盒,用手摸一摸长方体表面,观察6个面分别是什么形状,并标出“上、下、前、后、左、右”。
3)想一想,长方体和正方体的表面积与这6个面有什么
关系呢?
长方体或正方体6个面的总面积,叫做它的表面积。
3、自主探究,深化主题
上下、左右、前后各个面的长和宽分别是原长方体的什么?
一个长方体剪开的每个面是什么形状?展开后哪两个面是相对的面,有几组相等的面?
下
后
上
前
左
右
观察长方体展开图,分小组带着问题讨论:
前
上下面:长×宽×2
前后面:长×高×2
左右面:高×宽×2
上
下
左
右
后
做一个微波炉的包装箱,至少要用多少平方米的硬纸板
0.7m
0.5m
0.4m
这里要求的是这个长方体包装箱的表面积。
上、下每个面,长_____,宽_____,面积是_______;
前、后每个面,长_____,宽_____,面积是_______;
左、右每个面,长_____,宽_____,面积是_______。
0.7m
0.5m
0.35m2
0.7m
0.4m
0.28m2
0.5m
0.4m
0.2m2
4、教学例1
0.7m
0.5m
0.4m
这个包装箱的表面积是:
0.35×2+0.28×2+0.2×2
=0.7+0.56+0.4
=1.66(m2)
答:至少要用1.66m2硬纸板。
说一说:你是怎么计算的?
解法一:0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
= 0.35×2+0.28×2+0.2×2
=0.7+0.56+0.4
=1.66(m2)
解法二:(0.7×0.5+0.7×0.4+0.5×0.4)×2
=(0.35+0.28+0.2)×2
=0.83×2
= 1.66(m2)
这两种解法有什么不同?有什么联系?
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
长方体的表面积=(长×宽+长×高+宽×高)×2
S=2(a×b+a×h+b×h)
一个正方体墨水盒,棱长6.5cm。制作这个墨水盒至少需要多少平方厘米的硬纸板?
6.5×6.5×6
=42.25×6
=253.5(cm2)
答:制作这个墨水盒至少需要253.5cm2的硬纸板。
求至少用多少平方厘米的硬纸板,就是要求什么 自己试一试!
5、教学例2
正方体表面积=棱长×棱长×6
S=6a2
想一想,正方体表面积的计算方法是什么?
制作右面这样一个长方体纸盒。至少要用多少平方厘米的纸板?
5cm
4cm
8cm
8×5 ×2 +8×4 ×2 +5×4×2
=80+64+40
=184(平方厘米)
答:至少要用184平方厘米的纸板。
(三)综合实践,学以致用
1、基础练习
2、巩固提高
(1) 亮亮家要给一个长0.75m,宽0.5m,高1.6m的简易衣柜换布罩(如下图,没有底面)。至少需要用布多少平方米
0.75m
0.5m
1.6m
(2) 一个玻璃鱼缸的形状是正方体,棱长3dm。制作这个鱼缸时至少需要玻璃多少平方分米 (鱼缸的上面没有盖。)
3×3×5=45(dm2)
答:制作这个鱼缸时至少需要玻璃45dm2。
想一想,在日常生活中,做哪些事与求长方体、正方体的部分面积有关?
3.拓展延伸
小组合作:
测量火柴盒的长、宽、高,并计算做这样一个
火柴盒需要多少纸板?
(四)课堂小结
谈谈你在本节课中收获到了什么?
长方体和正方体的表面积
正方体的表面积=棱长×棱长×6
长方体上面(或下面)的面积=长×宽
长方体前面(或后面)的面积=长×高
长方体左面(或右面)的面积=宽×高
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2
或=(长×宽+长×高+高×宽)× 2
长方体或正方体6个面的总面积,叫做它的表面积。
S=2(a×b+a×h+b×h)
S=6a2
(五)教学反思
本节课教学也存在一定的不足,例如,优生在课堂上仍是主角,学困生由于动手能力差,思维跟不上,大部分时间只能充当观众与听众,从课堂练习可以看出他们对所学的知识一知半解,课堂如果让他们充分动手操作与表达,又会花费大量的时间,如何解决这样的矛盾,仍是我今后的重要研究内容。
