2023届高考物理专题复习:微元法在物理解题中应用课件(共22张PPT)
文档属性
| 名称 | 2023届高考物理专题复习:微元法在物理解题中应用课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 837.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-21 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
微元法
在高中物理解题中应用
1.如图,在质量为M=0.99kg的小车上固定着一个质量为m=10g、电阻R=1 的矩形单匝线圈MNPQ,其中MN边水平,NP边竖直,高度l=0.05m。小车载着线圈在光滑水平面上一起以v0=10m/s的速度做匀速运动,随后进入一水平有界匀强磁场(磁场宽度大于小车长度),完全穿出磁场时小车速度v1=2m/s。磁场方向与线圈平面垂直并指向纸内、磁感应强度大小B=1.0T。已知线圈与小车之间绝缘,小车长度与线圈MN边长度相同。求: (1)小车刚进入磁场时线圈中感应电流I的大小和方向;
(2)小车通过磁场的过程中线圈电阻的发热量Q;
(3)小车进入磁场过程中线圈克服安培力所做的功W。
解:(1)线圈切割磁感线的速度v0=10m/s,
感应电动势 E=Blv0=1×0.05×10=0.5V
线圈中电流
由楞次定律知线圈中感应电流方向为 M→Q→P→N→M
l
B
M
N
Q
P
v0
x
x
x
x
x
x
x
x
x
x
x
x
(2)线圈进出减小的动能转化为电热
?
一、微元法:
它是将研究对象(物体或物理过程)进行无限细分,从其中抽取某一微小单元即“元过程”进行讨论,每个“元过程”所遵循的规律是相同的。对这些“元过程”进行必要的数学方法或物理思想处理,进而使问题求解
二、挖掘教材中微元素材,认知微元思想
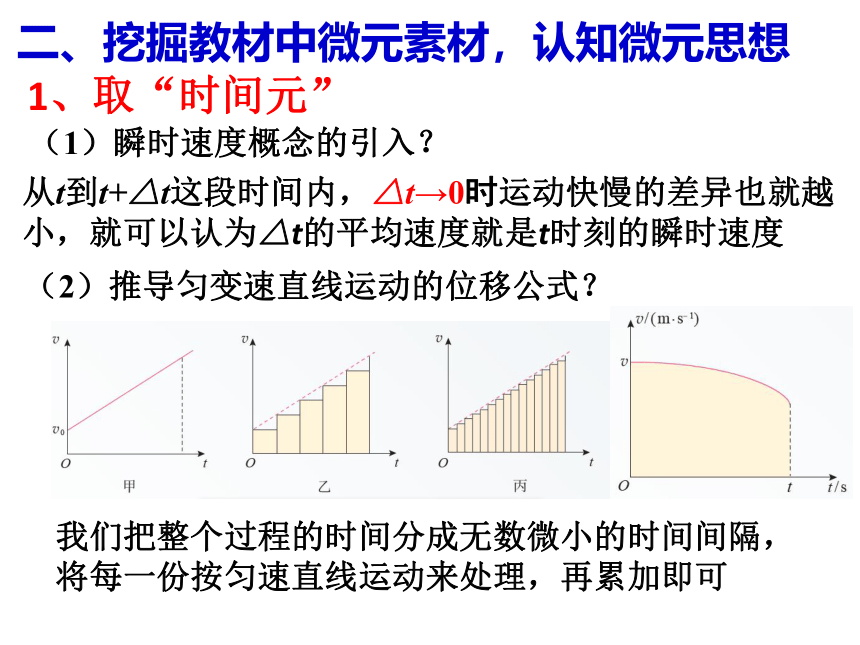
(1)瞬时速度概念的引入?
(2)推导匀变速直线运动的位移公式?
从t到t+△t这段时间内,△t→0时运动快慢的差异也就越小,就可以认为△t的平均速度就是t时刻的瞬时速度
我们把整个过程的时间分成无数微小的时间间隔,将每一份按匀速直线运动来处理,再累加即可
1、取“时间元”
1.如图,在质量为M=0.99kg的小车上固定着一个质量为m=10g、电阻R=1 的矩形单匝线圈MNPQ,其中MN边水平,NP边竖直,高度l=0.05m。小车载着线圈在光滑水平面上一起以v0=10m/s的速度做匀速运动,随后进入一水平有界匀强磁场(磁场宽度大于小车长度),完全穿出磁场时小车速度v1=2m/s。磁场方向与线圈平面垂直并指向纸内、磁感应强度大小B=1.0T。已知线圈与小车之间绝缘,小车长度与线圈MN边长度相同。求: (1)小车刚进入磁场时线圈中感应电流I的大小和方向;
(2)小车通过磁场的过程中线圈电阻的发热量Q;
(3)小车进入磁场过程中线圈克服安培力所做的功W。
解:(1)线圈切割磁感线的速度v0=10m/s,
感应电动势 E=Blv0=1×0.05×10=0.5V
线圈中电流
由楞次定律知线圈中感应电流方向为 M→Q→P→N→M
l
B
M
N
Q
P
v0
x
x
x
x
x
x
x
x
x
x
x
x
(2)线圈进出减小的动能转化为电热
?
(3)设小车完全进入磁场后速度为v,在小车进入磁场从t 时刻到
t+⊿t 时刻(⊿t→0)过程中,牛二定律:
即:
再对进场的整个进场过程求和得
同理
而
又线圈进、出磁场过程中磁通量的变化量相同,故 q入= q出
故得 v- v0= v 1-v
即:
所以小车进入磁场过程中线圈克服安培力做功
l
B
M
N
Q
P
v0
x
x
x
x
x
x
x
x
x
x
x
x
v
v
v1
——微元思想:
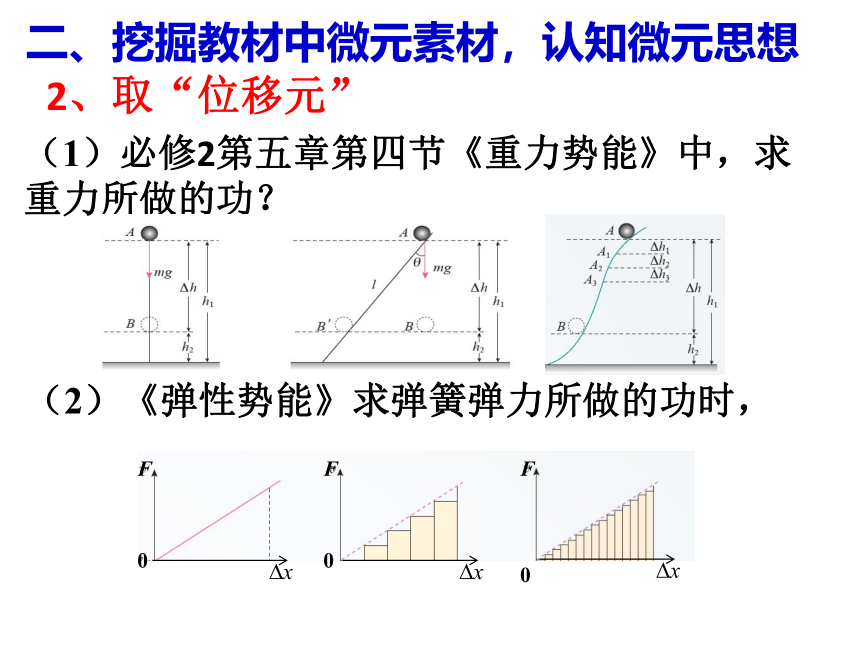
(1)必修2第五章第四节《重力势能》中,求重力所做的功?
二、挖掘教材中微元素材,认知微元思想
2、取“位移元”
(2)《弹性势能》求弹簧弹力所做的功时,
0
F
0
F
0
F
例2、如图水平细杆MN、CD长度均为L,两杆间距为h,M、C两端与半圆形细杆相连,半圆形细杆与MN、CD在同一竖直平面内,且MN、CD恰为半圆弧在M、C两点处的切线。质量为m的带正电的小球P,电荷量为q,穿在细杆上,已知小球P与两水平细杆间的动摩擦因数为μ,小球P与半圆形细杆之间绝缘且摩擦不计,(1)若整个装置处在方向与之垂直、磁感应强度为B的匀强磁场中,如图(甲)所示。小球P以一定的初速度v0从D端出发,沿杆滑到M点以后恰好在细杆MN上匀速运动。求:
①小球P在细杆MN上滑行的速度;
②小球P滑过DC杆的过程中克服摩擦力所做的功;
解(1)加B:
①从D→M后匀速
即: mg=Bqv
②在D→C阶段Wf:即D→M的Wf
故从D→M由动能定理:
G
fB
(2)撤去磁场,在MD、NC连线的交点O处固定一电荷量为Q的负电荷,如图(乙)所示,使小球P从D端出发沿杆滑动,滑到N点时速度恰好为零。(已知小球所受库仑力始终小于重力)求:
①小球P在水平细杆MN或CD上滑动时所受摩擦力的最大值和最小值;②小球P从D端出发时的初速度。
解(2)加E ① :
mg+F
N
f
F
mg
N
f
(2)②小球从D→N点时速度恰为零,由动能定理
整段由对称性及微元法有:
?
-Q
D
C
M
N
mg
F
mg
F
取微元有:
再对微元求和:
由对称性有 :
①选取微元用以量化元事物或元过程;
②视元事物或元过程为恒定,运用相应的规律给出待求量对应的微元表达式;
③在微元表达式的定义域内施以叠加演算,进而求得待求量。
三、微元法解题基本步骤:
练习1 如图,水平放置的导体电阻为R ,R与两根光滑的平行金属导轨相连,导轨间距为L ,其间有垂直导轨平面的、磁感应强度为B的匀强磁场。导轨上有一导体棒ab质量为m以初速度v0向右运动。求:
⑴导体棒在整个运动过程中的位移x
⑵导体棒整个运动过程中通过闭合回路的电量
fA
解:由牛二定律得
取微元,极短时间有:
求和有:
⑵导体棒整个运动过程中通过闭合回路的电量
即:
取微元,极短时间有:
求和有:
总结:
对棒受安培力微元求和,可以求全过程位移或电量
或直接由推导式求
2.随着电磁技术的日趋成熟,新一代航母已准备采用全新的电磁阻拦技术,它的原理是,飞机着舰时利用电磁作用力使它快速停止。为研究问题的方便,我们将其简化为如图所示的模型。在磁感应强度为B、方向如图所示的匀强磁场中,两根平行金属轨道MN、PQ 固定在水平面内,相距为L,电阻不计。轨道端点MP间接有阻值为R的电阻。一个长为L、质量为m、阻值r为 的金属导体棒 ab垂直于MN、PQ 放在轨道上,与轨道接触良好。飞机着舰时质量为M 的飞机迅速钩住导体棒 ,钩住之后关闭动力系统并立即获得共同的速度v,忽略摩擦等次要因素,飞机和金属棒系统仅在安培力作用下很快停下来。求
(1)飞机在阻拦减速过程中获得的加速度a的最大值;
(2)从飞机与金属棒共速到它们停下来的整个过程中 上产生的焦耳热 Q;
(3)从飞机与金属棒共速到它们停下来的整个过程中运动的距离 x
m
M
fA
解(1)刚开始共同v时,安培阻力提供的加速度最大
(2)从v→停下整个过程产生的总电热为
(3)从共速v开始变减速运动→停下过程中
取一极短微元时间,由牛二定律有
对整个过程求和:
x
0-v
3、如图,两根足够长的光滑固定平行金属导轨与水平面成θ角,导轨间距为d,两导体棒a和b与导轨垂直放置,两根导体棒的质量都为m、电阻都为R,回路中其余电阻不计。整个装置处于垂直于导轨平面向上的匀强磁场中,磁感应强度的大小为B。在t =0时刻使a沿导轨向上作速度为v的匀速运动,同时将b由静止释放,b经过一段时间后也作匀速运动。已知d =1m,m = 0.5kg,R =0.5Ω,B=0.5T,θ=30°,g取10m/s2,不计两导棒间的相互作用力。
⑴为使导体棒b能沿导轨向下运动,a的速度v不能超过多大?
⑵若a在平行于导轨向上的力F作用下,以v1=2m/s的速度沿导轨向上运动,试导出F与b的速率v2的函数关系式并求出v2的最大值; ⑶在⑵中,当t =2s时,b的速度达到5.06m/s,2s内回路中产生的焦耳热为13.2J,求该2s内力F做的功(结果保留三位有效数字)。
b
B
F
a
θ
θ
解:⑴设a的速度为v1,由于b初速度为零,则
对b:
FA<mgsinθ
联立解得:v1<10m/s
b
B
F
a
θ
θ
⑵设a的速度为v1,b的速度为v2,回路电流为I,
对a:mgsinθ + FA = F
代入数据得:
设b的最大速度为vm,则有:
代入数据得: vm= 8m/s
⑶对b:mgsinθ-FA= ma
取任意无限小△t时间:
代入数据并求和得:
8t-x2 = 2v2
将t=2s,v2=5.06m/s代入得:x2=5.88m
a位移:x1=v1t = 2×2 = 4m
a、b由功能关系知:
代入数据得:WF=14.9J
4、如图所示,两平行的光滑金属导轨安装在一光滑绝缘斜面上,导轨间距为L,电阻忽略不计且足够长,导轨平面的倾角为α,斜面上相隔为d的平行虚线MN与PQ间有磁感应强度大小为B的匀强磁场,方向与导轨平面垂直。另有一长为2d的绝缘杆将一导体棒和一边长为d(d(1)在装置第一次下滑的过程中,线框中产生的热量Q;
(2)画出整个装置在第一次下滑过程中
的速度-时间(v-t)图像;
(3)装置最终在斜面上做往复运动
的最大速率vm ;
(4)装置最终在斜面上做往复运动
的周期T 。
(1)从开始释放到棒到达MN速度减为0
v
t
O
(2)
t1
t2
t3
0-t1:导线框进磁场--出磁场
t1-t2:导线框出磁场--棒进磁场
t2-t3:棒进磁场--棒出磁场
(3)“最终”线框不能进磁场(消耗能量)
故最终最高点——恰线圈进不了磁场,1处
1
2
vm
最终最低点——棒处在MN、PQ之间某处,且v=0时,(3处,到不了MN处了 )
3
故从1→2处:机械能守恒有
(4)
1→2:
2→3:
补充:(2)线框第一次穿越磁场区域所需的时间t1 ;
(3)经过足够长时间后,线框上边与磁场区域下边界的最大距离
1
2
3
解(2)图中位置1处第一次到此处速度≠0,设为v1
则接着向下运动2d,v=0,由动能定理
线圈第一次穿磁场时受到的合力
由牛顿第二定律,在t到t+ Δt时间内
(3)经过足够长时间后,线框在磁场下
边界与最大距离xm之间往复运动
xm
由动能定理:
xm
Xm-d
5如图所示,两根相距为d的足够长的、光滑的平行金属导轨位于水平的xoy平面内,左端接有阻值为R的电阻,其他部分的电阻均可忽略不计。在x>0的一侧存在方向竖直向下的磁场,质量为m的金属杆电阻为r,与金属导轨垂直且接触良好。在x<0的某位置,金属杆受到一瞬时冲量,获得速度大小为v0,方向沿x轴正方向。求:
(1)金属杆运动过程中安培力对杆做的功及电阻R上产生焦耳热;
(2)若导轨间的磁场是匀强磁场,磁感应强度为B,导体杆最终静止时的坐标x1;
(3)若导轨间的磁场是非匀强磁场,磁感应强度B沿x轴正方向增加,且大小满足B2=kx,导体杆最终静止时的坐标x2;
(2)导轨间的磁场是匀强磁场,切割产生
安培力
(3)导轨间的磁场B2=kx ,
或动量定理微元
微元法
在高中物理解题中应用
1.如图,在质量为M=0.99kg的小车上固定着一个质量为m=10g、电阻R=1 的矩形单匝线圈MNPQ,其中MN边水平,NP边竖直,高度l=0.05m。小车载着线圈在光滑水平面上一起以v0=10m/s的速度做匀速运动,随后进入一水平有界匀强磁场(磁场宽度大于小车长度),完全穿出磁场时小车速度v1=2m/s。磁场方向与线圈平面垂直并指向纸内、磁感应强度大小B=1.0T。已知线圈与小车之间绝缘,小车长度与线圈MN边长度相同。求: (1)小车刚进入磁场时线圈中感应电流I的大小和方向;
(2)小车通过磁场的过程中线圈电阻的发热量Q;
(3)小车进入磁场过程中线圈克服安培力所做的功W。
解:(1)线圈切割磁感线的速度v0=10m/s,
感应电动势 E=Blv0=1×0.05×10=0.5V
线圈中电流
由楞次定律知线圈中感应电流方向为 M→Q→P→N→M
l
B
M
N
Q
P
v0
x
x
x
x
x
x
x
x
x
x
x
x
(2)线圈进出减小的动能转化为电热
?
一、微元法:
它是将研究对象(物体或物理过程)进行无限细分,从其中抽取某一微小单元即“元过程”进行讨论,每个“元过程”所遵循的规律是相同的。对这些“元过程”进行必要的数学方法或物理思想处理,进而使问题求解
二、挖掘教材中微元素材,认知微元思想
(1)瞬时速度概念的引入?
(2)推导匀变速直线运动的位移公式?
从t到t+△t这段时间内,△t→0时运动快慢的差异也就越小,就可以认为△t的平均速度就是t时刻的瞬时速度
我们把整个过程的时间分成无数微小的时间间隔,将每一份按匀速直线运动来处理,再累加即可
1、取“时间元”
1.如图,在质量为M=0.99kg的小车上固定着一个质量为m=10g、电阻R=1 的矩形单匝线圈MNPQ,其中MN边水平,NP边竖直,高度l=0.05m。小车载着线圈在光滑水平面上一起以v0=10m/s的速度做匀速运动,随后进入一水平有界匀强磁场(磁场宽度大于小车长度),完全穿出磁场时小车速度v1=2m/s。磁场方向与线圈平面垂直并指向纸内、磁感应强度大小B=1.0T。已知线圈与小车之间绝缘,小车长度与线圈MN边长度相同。求: (1)小车刚进入磁场时线圈中感应电流I的大小和方向;
(2)小车通过磁场的过程中线圈电阻的发热量Q;
(3)小车进入磁场过程中线圈克服安培力所做的功W。
解:(1)线圈切割磁感线的速度v0=10m/s,
感应电动势 E=Blv0=1×0.05×10=0.5V
线圈中电流
由楞次定律知线圈中感应电流方向为 M→Q→P→N→M
l
B
M
N
Q
P
v0
x
x
x
x
x
x
x
x
x
x
x
x
(2)线圈进出减小的动能转化为电热
?
(3)设小车完全进入磁场后速度为v,在小车进入磁场从t 时刻到
t+⊿t 时刻(⊿t→0)过程中,牛二定律:
即:
再对进场的整个进场过程求和得
同理
而
又线圈进、出磁场过程中磁通量的变化量相同,故 q入= q出
故得 v- v0= v 1-v
即:
所以小车进入磁场过程中线圈克服安培力做功
l
B
M
N
Q
P
v0
x
x
x
x
x
x
x
x
x
x
x
x
v
v
v1
——微元思想:
(1)必修2第五章第四节《重力势能》中,求重力所做的功?
二、挖掘教材中微元素材,认知微元思想
2、取“位移元”
(2)《弹性势能》求弹簧弹力所做的功时,
0
F
0
F
0
F
例2、如图水平细杆MN、CD长度均为L,两杆间距为h,M、C两端与半圆形细杆相连,半圆形细杆与MN、CD在同一竖直平面内,且MN、CD恰为半圆弧在M、C两点处的切线。质量为m的带正电的小球P,电荷量为q,穿在细杆上,已知小球P与两水平细杆间的动摩擦因数为μ,小球P与半圆形细杆之间绝缘且摩擦不计,(1)若整个装置处在方向与之垂直、磁感应强度为B的匀强磁场中,如图(甲)所示。小球P以一定的初速度v0从D端出发,沿杆滑到M点以后恰好在细杆MN上匀速运动。求:
①小球P在细杆MN上滑行的速度;
②小球P滑过DC杆的过程中克服摩擦力所做的功;
解(1)加B:
①从D→M后匀速
即: mg=Bqv
②在D→C阶段Wf:即D→M的Wf
故从D→M由动能定理:
G
fB
(2)撤去磁场,在MD、NC连线的交点O处固定一电荷量为Q的负电荷,如图(乙)所示,使小球P从D端出发沿杆滑动,滑到N点时速度恰好为零。(已知小球所受库仑力始终小于重力)求:
①小球P在水平细杆MN或CD上滑动时所受摩擦力的最大值和最小值;②小球P从D端出发时的初速度。
解(2)加E ① :
mg+F
N
f
F
mg
N
f
(2)②小球从D→N点时速度恰为零,由动能定理
整段由对称性及微元法有:
?
-Q
D
C
M
N
mg
F
mg
F
取微元有:
再对微元求和:
由对称性有 :
①选取微元用以量化元事物或元过程;
②视元事物或元过程为恒定,运用相应的规律给出待求量对应的微元表达式;
③在微元表达式的定义域内施以叠加演算,进而求得待求量。
三、微元法解题基本步骤:
练习1 如图,水平放置的导体电阻为R ,R与两根光滑的平行金属导轨相连,导轨间距为L ,其间有垂直导轨平面的、磁感应强度为B的匀强磁场。导轨上有一导体棒ab质量为m以初速度v0向右运动。求:
⑴导体棒在整个运动过程中的位移x
⑵导体棒整个运动过程中通过闭合回路的电量
fA
解:由牛二定律得
取微元,极短时间有:
求和有:
⑵导体棒整个运动过程中通过闭合回路的电量
即:
取微元,极短时间有:
求和有:
总结:
对棒受安培力微元求和,可以求全过程位移或电量
或直接由推导式求
2.随着电磁技术的日趋成熟,新一代航母已准备采用全新的电磁阻拦技术,它的原理是,飞机着舰时利用电磁作用力使它快速停止。为研究问题的方便,我们将其简化为如图所示的模型。在磁感应强度为B、方向如图所示的匀强磁场中,两根平行金属轨道MN、PQ 固定在水平面内,相距为L,电阻不计。轨道端点MP间接有阻值为R的电阻。一个长为L、质量为m、阻值r为 的金属导体棒 ab垂直于MN、PQ 放在轨道上,与轨道接触良好。飞机着舰时质量为M 的飞机迅速钩住导体棒 ,钩住之后关闭动力系统并立即获得共同的速度v,忽略摩擦等次要因素,飞机和金属棒系统仅在安培力作用下很快停下来。求
(1)飞机在阻拦减速过程中获得的加速度a的最大值;
(2)从飞机与金属棒共速到它们停下来的整个过程中 上产生的焦耳热 Q;
(3)从飞机与金属棒共速到它们停下来的整个过程中运动的距离 x
m
M
fA
解(1)刚开始共同v时,安培阻力提供的加速度最大
(2)从v→停下整个过程产生的总电热为
(3)从共速v开始变减速运动→停下过程中
取一极短微元时间,由牛二定律有
对整个过程求和:
x
0-v
3、如图,两根足够长的光滑固定平行金属导轨与水平面成θ角,导轨间距为d,两导体棒a和b与导轨垂直放置,两根导体棒的质量都为m、电阻都为R,回路中其余电阻不计。整个装置处于垂直于导轨平面向上的匀强磁场中,磁感应强度的大小为B。在t =0时刻使a沿导轨向上作速度为v的匀速运动,同时将b由静止释放,b经过一段时间后也作匀速运动。已知d =1m,m = 0.5kg,R =0.5Ω,B=0.5T,θ=30°,g取10m/s2,不计两导棒间的相互作用力。
⑴为使导体棒b能沿导轨向下运动,a的速度v不能超过多大?
⑵若a在平行于导轨向上的力F作用下,以v1=2m/s的速度沿导轨向上运动,试导出F与b的速率v2的函数关系式并求出v2的最大值; ⑶在⑵中,当t =2s时,b的速度达到5.06m/s,2s内回路中产生的焦耳热为13.2J,求该2s内力F做的功(结果保留三位有效数字)。
b
B
F
a
θ
θ
解:⑴设a的速度为v1,由于b初速度为零,则
对b:
FA<mgsinθ
联立解得:v1<10m/s
b
B
F
a
θ
θ
⑵设a的速度为v1,b的速度为v2,回路电流为I,
对a:mgsinθ + FA = F
代入数据得:
设b的最大速度为vm,则有:
代入数据得: vm= 8m/s
⑶对b:mgsinθ-FA= ma
取任意无限小△t时间:
代入数据并求和得:
8t-x2 = 2v2
将t=2s,v2=5.06m/s代入得:x2=5.88m
a位移:x1=v1t = 2×2 = 4m
a、b由功能关系知:
代入数据得:WF=14.9J
4、如图所示,两平行的光滑金属导轨安装在一光滑绝缘斜面上,导轨间距为L,电阻忽略不计且足够长,导轨平面的倾角为α,斜面上相隔为d的平行虚线MN与PQ间有磁感应强度大小为B的匀强磁场,方向与导轨平面垂直。另有一长为2d的绝缘杆将一导体棒和一边长为d(d
(2)画出整个装置在第一次下滑过程中
的速度-时间(v-t)图像;
(3)装置最终在斜面上做往复运动
的最大速率vm ;
(4)装置最终在斜面上做往复运动
的周期T 。
(1)从开始释放到棒到达MN速度减为0
v
t
O
(2)
t1
t2
t3
0-t1:导线框进磁场--出磁场
t1-t2:导线框出磁场--棒进磁场
t2-t3:棒进磁场--棒出磁场
(3)“最终”线框不能进磁场(消耗能量)
故最终最高点——恰线圈进不了磁场,1处
1
2
vm
最终最低点——棒处在MN、PQ之间某处,且v=0时,(3处,到不了MN处了 )
3
故从1→2处:机械能守恒有
(4)
1→2:
2→3:
补充:(2)线框第一次穿越磁场区域所需的时间t1 ;
(3)经过足够长时间后,线框上边与磁场区域下边界的最大距离
1
2
3
解(2)图中位置1处第一次到此处速度≠0,设为v1
则接着向下运动2d,v=0,由动能定理
线圈第一次穿磁场时受到的合力
由牛顿第二定律,在t到t+ Δt时间内
(3)经过足够长时间后,线框在磁场下
边界与最大距离xm之间往复运动
xm
由动能定理:
xm
Xm-d
5如图所示,两根相距为d的足够长的、光滑的平行金属导轨位于水平的xoy平面内,左端接有阻值为R的电阻,其他部分的电阻均可忽略不计。在x>0的一侧存在方向竖直向下的磁场,质量为m的金属杆电阻为r,与金属导轨垂直且接触良好。在x<0的某位置,金属杆受到一瞬时冲量,获得速度大小为v0,方向沿x轴正方向。求:
(1)金属杆运动过程中安培力对杆做的功及电阻R上产生焦耳热;
(2)若导轨间的磁场是匀强磁场,磁感应强度为B,导体杆最终静止时的坐标x1;
(3)若导轨间的磁场是非匀强磁场,磁感应强度B沿x轴正方向增加,且大小满足B2=kx,导体杆最终静止时的坐标x2;
(2)导轨间的磁场是匀强磁场,切割产生
安培力
(3)导轨间的磁场B2=kx ,
或动量定理微元
同课章节目录
