广东省河源市龙川县宏图学校2022-2023学年高一下学期5月月考数学试题(含解析)
文档属性
| 名称 | 广东省河源市龙川县宏图学校2022-2023学年高一下学期5月月考数学试题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 00:00:00 | ||
图片预览




文档简介
宏图学校2022-2023学年高一下学期5月月考
数学
注意事项:
1.答题前 考生务必将自己的姓名 考生号 考场号 座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
4.本试卷主要考试内容:人教A版必修第一册5.3~5.7,必修第二册6.1~8.3.
一 选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.( )
A. B. C. D.
2.( )
A. B. C. D.
3.已知向量的夹角为,且,则( )
A. B. C.3 D.6
4.设的内角的对边分别为,若,则( )
A. B. C. D.
5.已知向量,若向量在向量上的投影向量为,则( )
A. B. C. D.
6.已知函数,则( )
A.将的图象向右平移个单位长度可以得到的图象
B.将的图象向右平移个单位长度可以得到的图象
C.将的图象向右平移个单位长度可以得到的图象
D.将的图象向右平移个单位长度可以得到的图象
7.水果盘逐渐成为了很多家庭中常见的一种生活用品,它环保又美观,受到了大众的喜爱,而且水果盘逐渐由简单的盛物品变成带有摆饰风格的装饰品.水果盘的造型多样,如图所示的水果盘可以近似看成一个正六棱台,厚度忽略不计,它的上端是棱长为的正六边形开口,下端是棱长为的正六边形的封闭底面,侧面是6个封闭的等腰梯形,水果盘的高为,则该水果盘的容积为( )
A. B. C. D.
8.设的内角的对边分别为,且,若角的内角平分线,则的最小值为( )
A.8 B.4 C.16 D.12
二 多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知函数,则( )
A.
B.为奇函数
C.图象的对称中心为
D.的定义域为.
10.已知复数满足,则( )
A.的实部为-1 B.的虚部为2或-2
C. D.
11.如图,在平行四边形中,为的中点,,则( )
A. B.
C. D.
12.设符号函数知函数,则( )
A.为的周期
B.图象的对称轴方程为
C.在上单调递增
D.函数在上有6个零点
三 填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.已知向量,则与夹角的余弦值为__________.
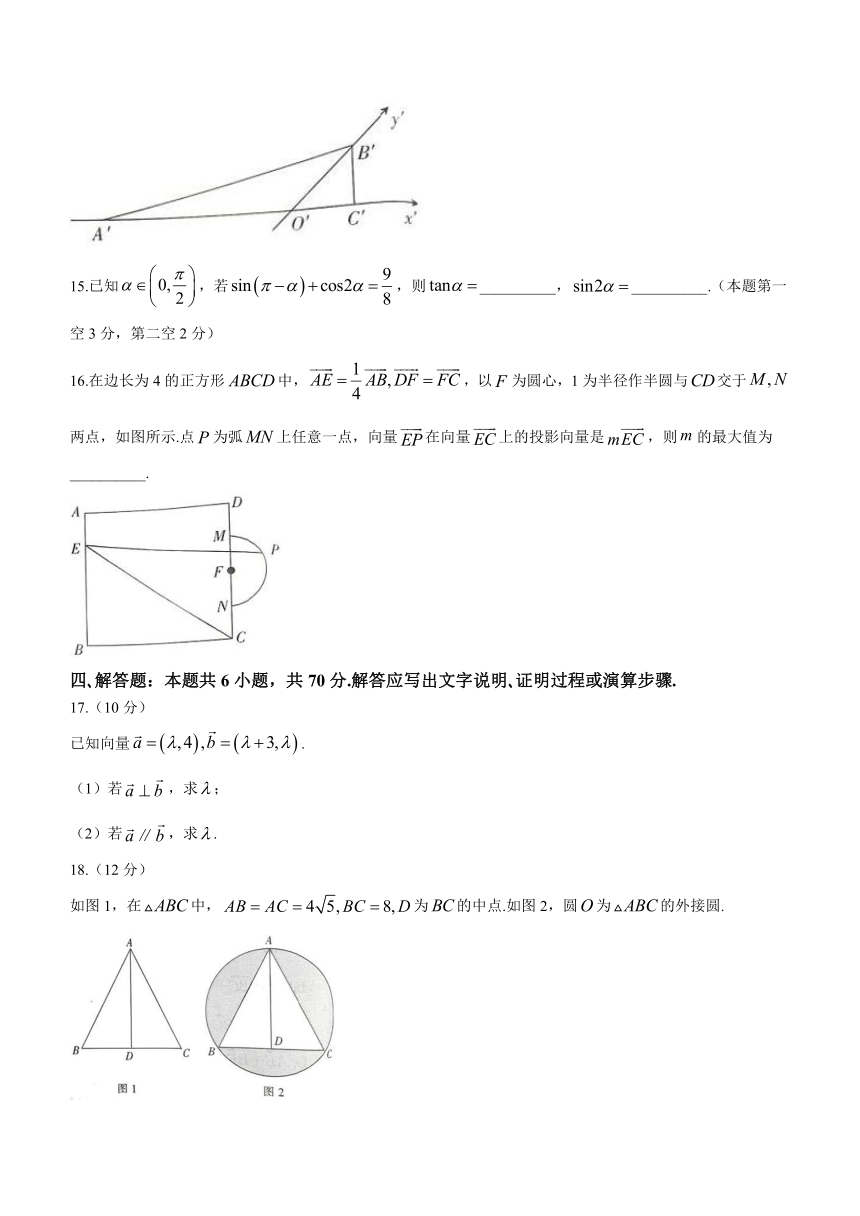
14.如图,直角是水平放置的的直观图,对应直角坐标系中的坐标原点,则__________.
15.已知,若,则__________,__________.(本题第一空3分,第二空2分)
16.在边长为4的正方形中,,以为圆心,1为半径作半圆与交于两点,如图所示.点为弧上任意一点,向量在向量上的投影向量是,则的最大值为__________.
四 解答题:本题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤.
17.(10分)
已知向量.
(1)若,求;
(2)若,求.
18.(12分)
如图1,在中,为的中点.如图2,圆为的外接圆.
(1)将图1中的绕着直线旋转得到一个几何体,求所得几何体的表面积;
(2)将图2中的阴影部分绕着直线旋转得到一个几何体,求所得几何体的体积.
19.(12分)
已知函数的部分图象如图所示.
(1)求的解析式;
(2)求在上的值域.
20.(12分)
已知函数.
(1)将的解析式化简成的形式;
(2)解不等式.
21.(12分)
在中,角的对边分别为,已知.
(1)求角;
(2)若边上的中线,且,求.
22.(12分)
如图,马鞍山长江公铁大桥是巢马城际铁路控制性工程,总长3248米,为世界上首座双主跨超千米的三塔斜拉桥,同时也是世界上最长联钢桁梁斜拉桥.为了解桥的一些结构情况,某学校道路桥梁工程设计学习小组将大桥的结构进行了简化,取其部分抽象成图中所示的模型,其中为其中两座桥塔的高,通过测量得知米,米,点在线段上,且在点处测得的顶端的仰角为,在点处测得的顶端的仰角为 .当时,.
(1)求主塔的高的长度.
(2)是否存在点,使得?如果存在,求出点的位置;如果不存在,请说明理由.
高一数学参考答案
1.A
2.C .
3.D 因为,所以.
4.D 因为,所以,则.由,得,所以
5.B 向量在向量上的投影向量为.
6.C 因为,所以将的图象向右平移个单位长度可以得到的图象,将的图象向左平移个单位长度可以得到的图象.
7.B 该水果盘的容积.
8.A 因为,所以,又,所以.
由,得,所以,
则,当且仅当时,等号成立.因为,所以的最小值为8.
9.ABD ,A正确.为奇函数,B正确.
令,则,所以图象的对称中心为,C错误.令,则,所以的定义域为正确.
10.ABC 因为,所以,得,所以的实部为正确;的虚部为-2或2,B正确;,C正确;当时,,当时,错误.
11.BCD 错误;
,B正确;
,
正确;
,D正确.
12.ABD 画出的部分图象,如图所示,
则为的周期,图象的对称轴方程为在上先单调递增,再单调递减,函数在上有6个零点.
13. 设与的夹角为,则.
14. 画出原图,如图所示.
易得是等腰直角三角形,则.
因为是直角三角形,,所以.
15. 因为,所以,又因为,所以,得.
16. 过作交于点,根据投影向量的概念可得.
当与半圆相切时,取得最大值.过作交于点,连接,当取得最大值时,且1
因为,所以,则,所以,得,所以的最大值为.
17.解:(1)因为,所以,
即,
解得或-7.
(2)因为,所以,
即,
解得或-2.
18.解:(1)因为为的中点,
所以
若将图1中的绕着直线旋转,
则所得几何体是一个底面半径为4,高为8的圆锥.
该圆锥的侧面积为,
该圆锥的底面积为,
所以所得几何体的表面积为.
(2)将图2中的阴影部分绕着直线旋转得到的几何体为
一个球挖去一个圆锥.
由题意可得外接圆的圆心在直线上,
设外接圆的半径为,则球的半径为.
,由,解得,
所以球的体积为,
圆锥的体积为,
故所得几何体的体积为.
19.解:(1)由的图象可知,,
,解得.
又因为的图象过点,所以,
则,解得.
又因为,所以.
故的解析式为.
(2)因为,所以,
所以当时,,
当时,,
故在上的值域为.
20.解:(1)
.
(2)令,得,
则,
解得,
故不等式的解集为.
21.解:(1)由题意知,
根据正弦定理,可得,即,
又由余弦定理得
因为,所以
(2)在中,根据余弦定理可得,
则,
解得或,
则或,因为,所以.
在中,由余弦定理可得.
22.解:(1)由题意可知.
因为,所以,
则米,
米,
米.
(2)设米,则
则.
令,则.
设,
因为,所以方程在上无解,所以不存在这样的点,使得.
数学
注意事项:
1.答题前 考生务必将自己的姓名 考生号 考场号 座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
4.本试卷主要考试内容:人教A版必修第一册5.3~5.7,必修第二册6.1~8.3.
一 选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.( )
A. B. C. D.
2.( )
A. B. C. D.
3.已知向量的夹角为,且,则( )
A. B. C.3 D.6
4.设的内角的对边分别为,若,则( )
A. B. C. D.
5.已知向量,若向量在向量上的投影向量为,则( )
A. B. C. D.
6.已知函数,则( )
A.将的图象向右平移个单位长度可以得到的图象
B.将的图象向右平移个单位长度可以得到的图象
C.将的图象向右平移个单位长度可以得到的图象
D.将的图象向右平移个单位长度可以得到的图象
7.水果盘逐渐成为了很多家庭中常见的一种生活用品,它环保又美观,受到了大众的喜爱,而且水果盘逐渐由简单的盛物品变成带有摆饰风格的装饰品.水果盘的造型多样,如图所示的水果盘可以近似看成一个正六棱台,厚度忽略不计,它的上端是棱长为的正六边形开口,下端是棱长为的正六边形的封闭底面,侧面是6个封闭的等腰梯形,水果盘的高为,则该水果盘的容积为( )
A. B. C. D.
8.设的内角的对边分别为,且,若角的内角平分线,则的最小值为( )
A.8 B.4 C.16 D.12
二 多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知函数,则( )
A.
B.为奇函数
C.图象的对称中心为
D.的定义域为.
10.已知复数满足,则( )
A.的实部为-1 B.的虚部为2或-2
C. D.
11.如图,在平行四边形中,为的中点,,则( )
A. B.
C. D.
12.设符号函数知函数,则( )
A.为的周期
B.图象的对称轴方程为
C.在上单调递增
D.函数在上有6个零点
三 填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.已知向量,则与夹角的余弦值为__________.
14.如图,直角是水平放置的的直观图,对应直角坐标系中的坐标原点,则__________.
15.已知,若,则__________,__________.(本题第一空3分,第二空2分)
16.在边长为4的正方形中,,以为圆心,1为半径作半圆与交于两点,如图所示.点为弧上任意一点,向量在向量上的投影向量是,则的最大值为__________.
四 解答题:本题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤.
17.(10分)
已知向量.
(1)若,求;
(2)若,求.
18.(12分)
如图1,在中,为的中点.如图2,圆为的外接圆.
(1)将图1中的绕着直线旋转得到一个几何体,求所得几何体的表面积;
(2)将图2中的阴影部分绕着直线旋转得到一个几何体,求所得几何体的体积.
19.(12分)
已知函数的部分图象如图所示.
(1)求的解析式;
(2)求在上的值域.
20.(12分)
已知函数.
(1)将的解析式化简成的形式;
(2)解不等式.
21.(12分)
在中,角的对边分别为,已知.
(1)求角;
(2)若边上的中线,且,求.
22.(12分)
如图,马鞍山长江公铁大桥是巢马城际铁路控制性工程,总长3248米,为世界上首座双主跨超千米的三塔斜拉桥,同时也是世界上最长联钢桁梁斜拉桥.为了解桥的一些结构情况,某学校道路桥梁工程设计学习小组将大桥的结构进行了简化,取其部分抽象成图中所示的模型,其中为其中两座桥塔的高,通过测量得知米,米,点在线段上,且在点处测得的顶端的仰角为,在点处测得的顶端的仰角为 .当时,.
(1)求主塔的高的长度.
(2)是否存在点,使得?如果存在,求出点的位置;如果不存在,请说明理由.
高一数学参考答案
1.A
2.C .
3.D 因为,所以.
4.D 因为,所以,则.由,得,所以
5.B 向量在向量上的投影向量为.
6.C 因为,所以将的图象向右平移个单位长度可以得到的图象,将的图象向左平移个单位长度可以得到的图象.
7.B 该水果盘的容积.
8.A 因为,所以,又,所以.
由,得,所以,
则,当且仅当时,等号成立.因为,所以的最小值为8.
9.ABD ,A正确.为奇函数,B正确.
令,则,所以图象的对称中心为,C错误.令,则,所以的定义域为正确.
10.ABC 因为,所以,得,所以的实部为正确;的虚部为-2或2,B正确;,C正确;当时,,当时,错误.
11.BCD 错误;
,B正确;
,
正确;
,D正确.
12.ABD 画出的部分图象,如图所示,
则为的周期,图象的对称轴方程为在上先单调递增,再单调递减,函数在上有6个零点.
13. 设与的夹角为,则.
14. 画出原图,如图所示.
易得是等腰直角三角形,则.
因为是直角三角形,,所以.
15. 因为,所以,又因为,所以,得.
16. 过作交于点,根据投影向量的概念可得.
当与半圆相切时,取得最大值.过作交于点,连接,当取得最大值时,且1
因为,所以,则,所以,得,所以的最大值为.
17.解:(1)因为,所以,
即,
解得或-7.
(2)因为,所以,
即,
解得或-2.
18.解:(1)因为为的中点,
所以
若将图1中的绕着直线旋转,
则所得几何体是一个底面半径为4,高为8的圆锥.
该圆锥的侧面积为,
该圆锥的底面积为,
所以所得几何体的表面积为.
(2)将图2中的阴影部分绕着直线旋转得到的几何体为
一个球挖去一个圆锥.
由题意可得外接圆的圆心在直线上,
设外接圆的半径为,则球的半径为.
,由,解得,
所以球的体积为,
圆锥的体积为,
故所得几何体的体积为.
19.解:(1)由的图象可知,,
,解得.
又因为的图象过点,所以,
则,解得.
又因为,所以.
故的解析式为.
(2)因为,所以,
所以当时,,
当时,,
故在上的值域为.
20.解:(1)
.
(2)令,得,
则,
解得,
故不等式的解集为.
21.解:(1)由题意知,
根据正弦定理,可得,即,
又由余弦定理得
因为,所以
(2)在中,根据余弦定理可得,
则,
解得或,
则或,因为,所以.
在中,由余弦定理可得.
22.解:(1)由题意可知.
因为,所以,
则米,
米,
米.
(2)设米,则
则.
令,则.
设,
因为,所以方程在上无解,所以不存在这样的点,使得.
同课章节目录
