四川省达州市2022-2023学年高一下学期5月第三次质量监测数学试题(含解析)
文档属性
| 名称 | 四川省达州市2022-2023学年高一下学期5月第三次质量监测数学试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 15:03:37 | ||
图片预览




文档简介
达州市2022-2023学年高一下学期5月第三次质量监测
(数学)试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的。
1.已知复数满足,则的虚部为( )
A. B. C.-2 D.2
2.设是平行四边形的对角线的交点,则( )
A. B. C. D.
3.已知,则( )
A. B. C. D.
4.工业生产者出厂价格指数(PPI)反映工业企业产品第一次出售时的出厂价格的变化趋势和变动幅度,对企业的生产发展和国家宏观调控有着重要的影响.下图是我国2022年各月PPI涨跌幅折线图.(注:下图中,月度同比是将上年同月作为基期相比较的增长率;月度环比是将上月作为基期相比较的增长率)
下列说法中,最贴切的一项为( )
A.2021年PPI逐月减小
B.2022年PPI逐月减小
C.2022年各月PPI同比涨跌幅的方差小于环比涨跌幅的方差
D.2022年上半年各月PPI同比涨跌幅的方差小于下半年各月PPI同比涨跌幅的方差
5.若,则( )
A. B. C.或-1 D.或1
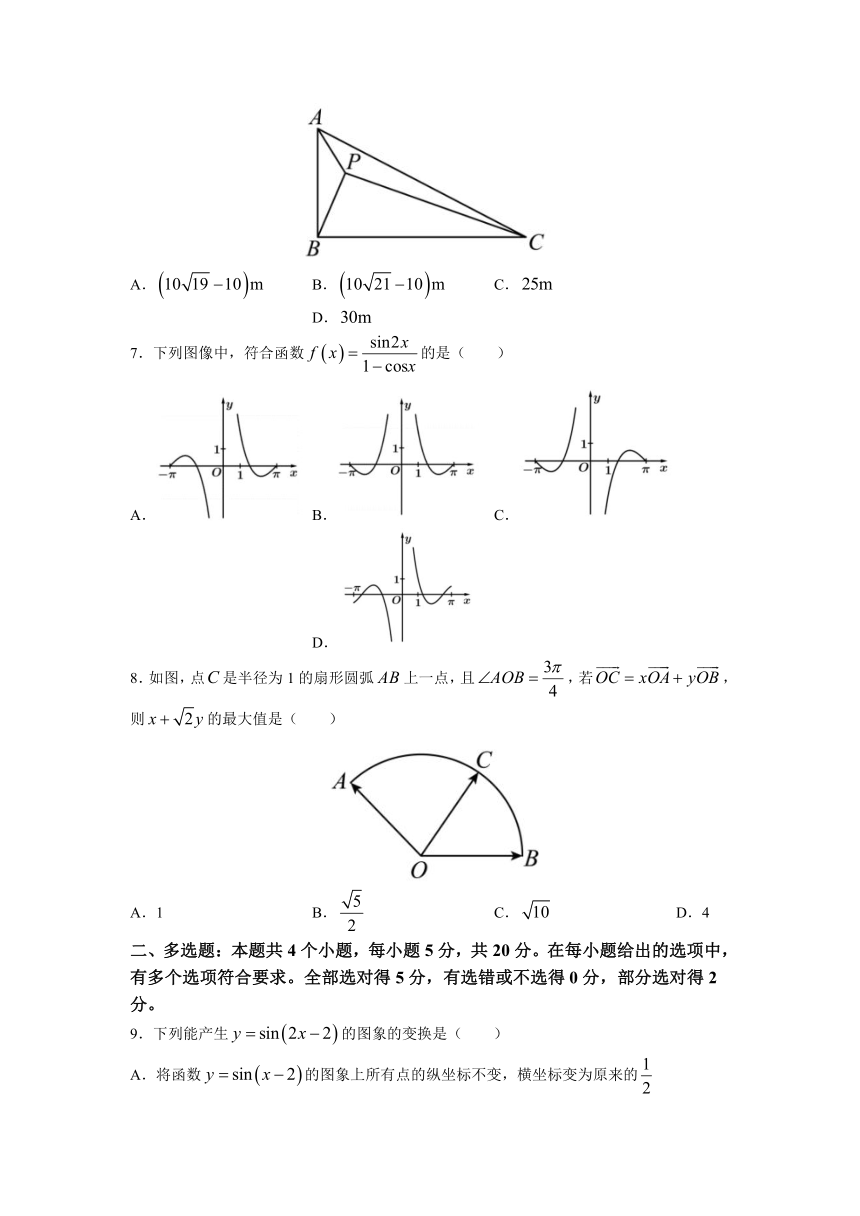
6.某园区有一块三角形空地(如图),其中,,,现计划在该空地上划分三个区域种植不同的花卉,若要求,则的最小值为( )
A. B. C. D.
7.下列图像中,符合函数的是( )
A. B. C. D.
8.如图,点是半径为1的扇形圆弧上一点,且,若,则的最大值是( )
A.1 B. C. D.4
二、多选题:本题共4个小题,每小题5分,共20分。在每小题给出的选项中,有多个选项符合要求。全部选对得5分,有选错或不选得0分,部分选对得2分。
9.下列能产生的图象的变换是( )
A.将函数的图象上所有点的纵坐标不变,横坐标变为原来的
B.将函数的图象上所有点的纵坐标不变,横坐标变为原来的
C.将函数的图象沿轴向左平移3个单位;
D.将函数的图象沿轴向右平移3个单位.
10.恩格尔系数是食品支出总额占个人消费支出总额的比重,恩格尔系数达以上为贫困,为温饱,为小康,为富裕,低于为最富裕.国家统计局2023年1月17日发布了我国2022年居民收入和消费支出情况,根据统计图表如图甲、乙所示,下列说法正确的是( )
A.2022年城镇居民人均可支配收入增长额超过农村居民人均可支配收入增长额
B.2022年城镇居民收入增长率快于农村居民
C.从恩格尔系数看,可认为我国2022年已达到富裕
D.2022年全国居民人均消费支出构成中食品烟酒和居住占比超过50%
11.在中,内角A,B,C所对的边分别为a,b,c,则下列结论正确的是( )
A.若,则
B.若,则是锐角三角形
C.若,则是等腰三角形
D.若为锐角三角形,则
12.点是所在平面内的一点,下列说法正确的有( )
A.若则为的重心
B.若,则点为的垂心
C.在中,向量与满足,且,则为等边三角形
D.若,,分别表示,的面积,则
三、填空题:本题共4小题,每小题5分,共20分。
13.如果复数满足,那么的最大值是_____.
14.设为的外心a,b,c分别为角A,B,C的对边,若,,则___________.
15.已知在中,内角A,B,C所对的边分别为a,b,c,且满足,且,则__________,___________.(第一空2分,第二空3分)
16.将函数的图象向左平移个单位长度,再把图象上的所有点的横坐标变为原来的倍,纵坐标不变,得到函数,已知函数在区间上单调递增,则的取值范围为____________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)设向量,.
(1)求在上的投影向量;
(2)若向量与向量的夹角为针角,求实数的取值范围.
18.(本小题满分12分)在①;②,这两个条件中任选一个,补充在下面问题中,并加以解答.
已知的内角A,B,C所对的边分别为a,b,c,____________.
(1)求的值;
(2)若的面积为2,,求的周长.
注:如选择多个条件分别解答,按第一个解答计分.
19.(本小题满分12分)已知函数.
(1)求函数的单调递增区间;
(2)设,,求的值.
20.(本小题满分12分)某地区突发小型地质灾害,为了了解该地区受灾居民的经济损失,制定合理的帮扶方案,研究人员经过调查后将该地区所有受灾居民的经济损失情况统计如下图所示.
(1)求a的值;
(2)求所有受灾居民的经济损失的平均值;
(3)现按照分层抽样的方法从经济损失在[4000,8000)的居民中随机抽取8人,则在[4000,6000)的居民有多少人.
21.(本小题满分12分)根据指令,机器人在平面上能完成下列动作:先原地旋转角度(按逆时针方向旋转时为正,按顺时针方向旋转时为负),再朝其面对的方向沿直线行走距离.
(1)机器人位于直角坐标系的坐标原点,且面对轴正方向,试给机器人下一个指令,使其移动到点;
(2)机器人在完成(1)中指令后,发现在点处有一小球正向坐标原点做匀速直线运动.已知小球运动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问:机器人最快可在何处截住小球?并给出机器人截住小球所需的指令(取).
22.(本小题满分12分)达州市人民公园有一块长方形空地,如图,,.为迎接“国庆”观光游,在边界上选择中点,分别在边界、上取M、N两点,现将三角形地块修建为花圃,并修建观赏小径,,,且.
(1)当时,求花圃的面积;
(2)求观赏小径与长度和的取值范围.
达州市2022-2023学年高一下学期5月第三次质量监测
(数学)答案
1.C ,故虚部为-2.
2.A 是平行四边形的对角线的交点,则,,
所以.
3.A .
4.D 对于A,由2022年10月,PPI同比为负可知,2021年10月PPI大于2022年10月PPI,
由2022年10月,PPI环比为正可知,2022年10月PPI大于2022年9月PPI,
由2022年9月,PPI同比为正可知,2022年9月PPI大于2021年9月PPI,
故2021年10月PPI大于2021年9月PPI,PPI逐月减小说法不正确,故选项A错误;
对于B,2022年2月、3月等月份,PPI环比均为正,相对于上月有增长,PPI逐月减小说法不正确,故选项B错误;
对于C,2022年PPI同比涨跌幅的数据波动幅度明显比环比涨跌幅的数据波动幅度要大,
因此2022年各月PPI同比涨跌幅的方差大于环比涨跌幅的方差,故选项C错误;
对于D,2022年上半年各月PPI同比涨跌幅的数据波动幅度明显比下半年各月PPI同比涨跌幅的数据波动幅度要小,
因此2022年上半年各月PPI同比涨跌幅的方差小于下半年各月PPI同比涨跌幅的方差,故选项D正确.
5.A ,
所以,得,
所以.
6.B 如图,因为,所以点在如图所示的圆上,
圆的半径为,
由圆周角的性质可得,,,
连接,可得(当为与圆的交点时,取等号),
在中,,,,根据余弦定理可知,所以的最小值为.
7.A 由知,
∴是奇函数,选项B错误;
,,所以选项C和选项D错误,选项A正确.
8.C 如图所示,以为轴,过作与垂直的线作为轴,
∵,,,∴,,
设,,
∴∴
∴
∴时,取得最大值是.
9.AD A:函数图象上所有的点纵坐标不变,横坐标变为原来的,
得函数的图象,故A正确;
B:函数图象上所有的点纵坐标不变,横坐标变为原来的,
得函数的图象,故B错误;
C:函数的图象沿轴向左平移3个单位,
得函数的图象,故C错误;
D:根据诱导公式函数的图象沿轴向右平移3个单位,
得函数的图象,故D正确.
10.ACD 对于选项A,从图甲可知,
2022年城镇居民人均可支配收入增长额为,
2022年农村居民人均可支配收入增长额为,
故A正确;
对于选项B,从图甲可知,
2022年城镇居民收入实际增速为,
2022年农村居民收入实际增速为,
故B错误.
对于选项C,从图乙可知,2022年食品支出总额占个人消费支出总额的比重,属于的范围,故C正确.
对于选项D,从图乙可知,2022年食品烟酒和居住占比为,故D正确.
11.AD 对于A项,在中,由正弦定理得:,,(为外接圆的半径),
因为,所以,所以,故A项正确;
所以B项,因为,所以,所以为锐角,但无法确定是否为锐角,故B项不成立;
对于C项,因为,
所以由正弦定理得:,即:,
所以或,
所以或,
所以为等腰三角形或直角三角形,故C项不成立;
对于D项,因为为锐角三角形,
所以,
又因为在上单调递增,
所以,即:,故D项正确.
故选:AD.
12.ACD
对于A,如图,取边中点,连接边上的中线,则,
又∵由,∴,∴,
∴O为的重心,故选项A正确;
对于B,如图,取边中点,边中点,连接,,
则,,
∵,∴,
∴,∴,,∴,,
∴,分别是,边上的垂直平分线,
∴,O为的外心,故选项B错误;
对于C,作角A的内角平分线与边交于点,
∵为方向的单位向量,为方向的单位向量,
∴,∴,
∴,∴,∴,为等腰三角形,
又∵,且,∴,
∴为等边三角形,故选项C正确;
对于D,设,,由得,
则由选项A可知,为的重心,设的面积,
∴,
又∵,,
,,,
,
∴,故选项D正确.
故选:ACD.
13.或 记复平面上数1对应点,复数对应点为,复数对应点为,则在以为圆心,1为半径的圆上,,点在圆外,
当点是直线与圆的交点(在,之间)时(如图),取得最大值.
故答案为:.
14.8 因为为的外心,
则,同理,
所以.
15.;或0.875
由题意,
根据正弦定理边角互化可得,
又因为,所以,
所以,
由,,解得,即,
所以根据余弦定理可得
16. 将函数的图象向左平移个单位长度得到的图象,
再将图象上每个点的横坐标变为原来的倍(纵坐标不变),
得到函数的图象,
∵函数在区间上单调递增,
所以,即,解得,①
又,
所以,解得,②
由①②可得,
故答案为:.
17.(1) (2)
(1)求在上的投影向量
(2)由已知,,,
所以,
因为向量与向量的夹角为钝角,
所以,,解得,
又因为向量不与向量反向共线,
设,则
从而或(舍去),所以解得.
18.(1) (2)
(1)若选①,由已知得,所以,
由正弦定理得,
又,所以,所以,又,
由,,解得.
若选②,由已知及正弦定理得,
所以,
所以,
所以,
又,所以,所以,又,
由,,解得.
(2)由的面积为2,得,所以,
由(1)可得,
由余弦定理得,
所以,所以,
所以的周长为.
19.(1),; (2).
(1),
令,,解得,,
所以的单调递增区间为,.
(2),
由得,
所以.
20.(1) (2)3360 (3)6
(1)依题意,,
解得.
(2)所有受灾居民经济损失的平均值为.
(3)由(1)可得经济损失在和在的人数比例为,由分层抽样知识可知,经济损失在的,人
21.(1)指令为
(2)机器人最快可在点处截住小球,指令为.
(1)如图,设点,所以,
因为与轴正方向的夹角为,
所以,,故指令为.
(2)设,机器人最快在点处截住小球,
由题意知,即,
整理得,即,
所以或(舍去),即机器人最快可在点处截住小球.
设与的夹角为,易知,,,
所以,所以.
因为由的方向旋转到的方向是顺时针旋转,所以指令为.
22.(1) (2)
由题可得,.
则.
故;
(2)设,则,
结合题意可知,则.
又,,
则,
令,则
,所以,
又,所以,因在上单调递增,在上单调递减,,
则.因为函数均在上单调递增,则函数在上单调递增,所以.
所以,即观赏小径与长度和的取值范围为.
(数学)试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的。
1.已知复数满足,则的虚部为( )
A. B. C.-2 D.2
2.设是平行四边形的对角线的交点,则( )
A. B. C. D.
3.已知,则( )
A. B. C. D.
4.工业生产者出厂价格指数(PPI)反映工业企业产品第一次出售时的出厂价格的变化趋势和变动幅度,对企业的生产发展和国家宏观调控有着重要的影响.下图是我国2022年各月PPI涨跌幅折线图.(注:下图中,月度同比是将上年同月作为基期相比较的增长率;月度环比是将上月作为基期相比较的增长率)
下列说法中,最贴切的一项为( )
A.2021年PPI逐月减小
B.2022年PPI逐月减小
C.2022年各月PPI同比涨跌幅的方差小于环比涨跌幅的方差
D.2022年上半年各月PPI同比涨跌幅的方差小于下半年各月PPI同比涨跌幅的方差
5.若,则( )
A. B. C.或-1 D.或1
6.某园区有一块三角形空地(如图),其中,,,现计划在该空地上划分三个区域种植不同的花卉,若要求,则的最小值为( )
A. B. C. D.
7.下列图像中,符合函数的是( )
A. B. C. D.
8.如图,点是半径为1的扇形圆弧上一点,且,若,则的最大值是( )
A.1 B. C. D.4
二、多选题:本题共4个小题,每小题5分,共20分。在每小题给出的选项中,有多个选项符合要求。全部选对得5分,有选错或不选得0分,部分选对得2分。
9.下列能产生的图象的变换是( )
A.将函数的图象上所有点的纵坐标不变,横坐标变为原来的
B.将函数的图象上所有点的纵坐标不变,横坐标变为原来的
C.将函数的图象沿轴向左平移3个单位;
D.将函数的图象沿轴向右平移3个单位.
10.恩格尔系数是食品支出总额占个人消费支出总额的比重,恩格尔系数达以上为贫困,为温饱,为小康,为富裕,低于为最富裕.国家统计局2023年1月17日发布了我国2022年居民收入和消费支出情况,根据统计图表如图甲、乙所示,下列说法正确的是( )
A.2022年城镇居民人均可支配收入增长额超过农村居民人均可支配收入增长额
B.2022年城镇居民收入增长率快于农村居民
C.从恩格尔系数看,可认为我国2022年已达到富裕
D.2022年全国居民人均消费支出构成中食品烟酒和居住占比超过50%
11.在中,内角A,B,C所对的边分别为a,b,c,则下列结论正确的是( )
A.若,则
B.若,则是锐角三角形
C.若,则是等腰三角形
D.若为锐角三角形,则
12.点是所在平面内的一点,下列说法正确的有( )
A.若则为的重心
B.若,则点为的垂心
C.在中,向量与满足,且,则为等边三角形
D.若,,分别表示,的面积,则
三、填空题:本题共4小题,每小题5分,共20分。
13.如果复数满足,那么的最大值是_____.
14.设为的外心a,b,c分别为角A,B,C的对边,若,,则___________.
15.已知在中,内角A,B,C所对的边分别为a,b,c,且满足,且,则__________,___________.(第一空2分,第二空3分)
16.将函数的图象向左平移个单位长度,再把图象上的所有点的横坐标变为原来的倍,纵坐标不变,得到函数,已知函数在区间上单调递增,则的取值范围为____________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)设向量,.
(1)求在上的投影向量;
(2)若向量与向量的夹角为针角,求实数的取值范围.
18.(本小题满分12分)在①;②,这两个条件中任选一个,补充在下面问题中,并加以解答.
已知的内角A,B,C所对的边分别为a,b,c,____________.
(1)求的值;
(2)若的面积为2,,求的周长.
注:如选择多个条件分别解答,按第一个解答计分.
19.(本小题满分12分)已知函数.
(1)求函数的单调递增区间;
(2)设,,求的值.
20.(本小题满分12分)某地区突发小型地质灾害,为了了解该地区受灾居民的经济损失,制定合理的帮扶方案,研究人员经过调查后将该地区所有受灾居民的经济损失情况统计如下图所示.
(1)求a的值;
(2)求所有受灾居民的经济损失的平均值;
(3)现按照分层抽样的方法从经济损失在[4000,8000)的居民中随机抽取8人,则在[4000,6000)的居民有多少人.
21.(本小题满分12分)根据指令,机器人在平面上能完成下列动作:先原地旋转角度(按逆时针方向旋转时为正,按顺时针方向旋转时为负),再朝其面对的方向沿直线行走距离.
(1)机器人位于直角坐标系的坐标原点,且面对轴正方向,试给机器人下一个指令,使其移动到点;
(2)机器人在完成(1)中指令后,发现在点处有一小球正向坐标原点做匀速直线运动.已知小球运动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问:机器人最快可在何处截住小球?并给出机器人截住小球所需的指令(取).
22.(本小题满分12分)达州市人民公园有一块长方形空地,如图,,.为迎接“国庆”观光游,在边界上选择中点,分别在边界、上取M、N两点,现将三角形地块修建为花圃,并修建观赏小径,,,且.
(1)当时,求花圃的面积;
(2)求观赏小径与长度和的取值范围.
达州市2022-2023学年高一下学期5月第三次质量监测
(数学)答案
1.C ,故虚部为-2.
2.A 是平行四边形的对角线的交点,则,,
所以.
3.A .
4.D 对于A,由2022年10月,PPI同比为负可知,2021年10月PPI大于2022年10月PPI,
由2022年10月,PPI环比为正可知,2022年10月PPI大于2022年9月PPI,
由2022年9月,PPI同比为正可知,2022年9月PPI大于2021年9月PPI,
故2021年10月PPI大于2021年9月PPI,PPI逐月减小说法不正确,故选项A错误;
对于B,2022年2月、3月等月份,PPI环比均为正,相对于上月有增长,PPI逐月减小说法不正确,故选项B错误;
对于C,2022年PPI同比涨跌幅的数据波动幅度明显比环比涨跌幅的数据波动幅度要大,
因此2022年各月PPI同比涨跌幅的方差大于环比涨跌幅的方差,故选项C错误;
对于D,2022年上半年各月PPI同比涨跌幅的数据波动幅度明显比下半年各月PPI同比涨跌幅的数据波动幅度要小,
因此2022年上半年各月PPI同比涨跌幅的方差小于下半年各月PPI同比涨跌幅的方差,故选项D正确.
5.A ,
所以,得,
所以.
6.B 如图,因为,所以点在如图所示的圆上,
圆的半径为,
由圆周角的性质可得,,,
连接,可得(当为与圆的交点时,取等号),
在中,,,,根据余弦定理可知,所以的最小值为.
7.A 由知,
∴是奇函数,选项B错误;
,,所以选项C和选项D错误,选项A正确.
8.C 如图所示,以为轴,过作与垂直的线作为轴,
∵,,,∴,,
设,,
∴∴
∴
∴时,取得最大值是.
9.AD A:函数图象上所有的点纵坐标不变,横坐标变为原来的,
得函数的图象,故A正确;
B:函数图象上所有的点纵坐标不变,横坐标变为原来的,
得函数的图象,故B错误;
C:函数的图象沿轴向左平移3个单位,
得函数的图象,故C错误;
D:根据诱导公式函数的图象沿轴向右平移3个单位,
得函数的图象,故D正确.
10.ACD 对于选项A,从图甲可知,
2022年城镇居民人均可支配收入增长额为,
2022年农村居民人均可支配收入增长额为,
故A正确;
对于选项B,从图甲可知,
2022年城镇居民收入实际增速为,
2022年农村居民收入实际增速为,
故B错误.
对于选项C,从图乙可知,2022年食品支出总额占个人消费支出总额的比重,属于的范围,故C正确.
对于选项D,从图乙可知,2022年食品烟酒和居住占比为,故D正确.
11.AD 对于A项,在中,由正弦定理得:,,(为外接圆的半径),
因为,所以,所以,故A项正确;
所以B项,因为,所以,所以为锐角,但无法确定是否为锐角,故B项不成立;
对于C项,因为,
所以由正弦定理得:,即:,
所以或,
所以或,
所以为等腰三角形或直角三角形,故C项不成立;
对于D项,因为为锐角三角形,
所以,
又因为在上单调递增,
所以,即:,故D项正确.
故选:AD.
12.ACD
对于A,如图,取边中点,连接边上的中线,则,
又∵由,∴,∴,
∴O为的重心,故选项A正确;
对于B,如图,取边中点,边中点,连接,,
则,,
∵,∴,
∴,∴,,∴,,
∴,分别是,边上的垂直平分线,
∴,O为的外心,故选项B错误;
对于C,作角A的内角平分线与边交于点,
∵为方向的单位向量,为方向的单位向量,
∴,∴,
∴,∴,∴,为等腰三角形,
又∵,且,∴,
∴为等边三角形,故选项C正确;
对于D,设,,由得,
则由选项A可知,为的重心,设的面积,
∴,
又∵,,
,,,
,
∴,故选项D正确.
故选:ACD.
13.或 记复平面上数1对应点,复数对应点为,复数对应点为,则在以为圆心,1为半径的圆上,,点在圆外,
当点是直线与圆的交点(在,之间)时(如图),取得最大值.
故答案为:.
14.8 因为为的外心,
则,同理,
所以.
15.;或0.875
由题意,
根据正弦定理边角互化可得,
又因为,所以,
所以,
由,,解得,即,
所以根据余弦定理可得
16. 将函数的图象向左平移个单位长度得到的图象,
再将图象上每个点的横坐标变为原来的倍(纵坐标不变),
得到函数的图象,
∵函数在区间上单调递增,
所以,即,解得,①
又,
所以,解得,②
由①②可得,
故答案为:.
17.(1) (2)
(1)求在上的投影向量
(2)由已知,,,
所以,
因为向量与向量的夹角为钝角,
所以,,解得,
又因为向量不与向量反向共线,
设,则
从而或(舍去),所以解得.
18.(1) (2)
(1)若选①,由已知得,所以,
由正弦定理得,
又,所以,所以,又,
由,,解得.
若选②,由已知及正弦定理得,
所以,
所以,
所以,
又,所以,所以,又,
由,,解得.
(2)由的面积为2,得,所以,
由(1)可得,
由余弦定理得,
所以,所以,
所以的周长为.
19.(1),; (2).
(1),
令,,解得,,
所以的单调递增区间为,.
(2),
由得,
所以.
20.(1) (2)3360 (3)6
(1)依题意,,
解得.
(2)所有受灾居民经济损失的平均值为.
(3)由(1)可得经济损失在和在的人数比例为,由分层抽样知识可知,经济损失在的,人
21.(1)指令为
(2)机器人最快可在点处截住小球,指令为.
(1)如图,设点,所以,
因为与轴正方向的夹角为,
所以,,故指令为.
(2)设,机器人最快在点处截住小球,
由题意知,即,
整理得,即,
所以或(舍去),即机器人最快可在点处截住小球.
设与的夹角为,易知,,,
所以,所以.
因为由的方向旋转到的方向是顺时针旋转,所以指令为.
22.(1) (2)
由题可得,.
则.
故;
(2)设,则,
结合题意可知,则.
又,,
则,
令,则
,所以,
又,所以,因在上单调递增,在上单调递减,,
则.因为函数均在上单调递增,则函数在上单调递增,所以.
所以,即观赏小径与长度和的取值范围为.
同课章节目录
