中考专题复习——有关“中点”考点建模

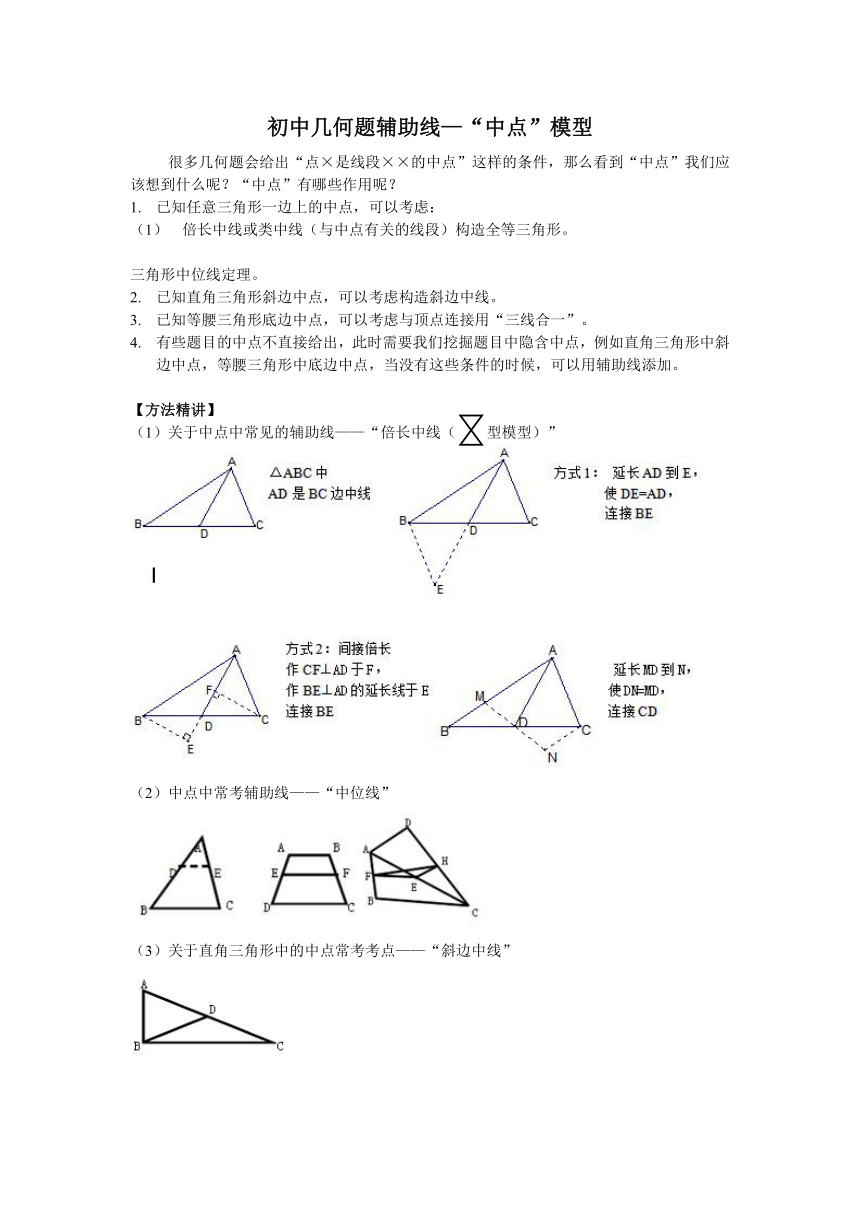
初中几何题辅助线—“中点”模型
很多几何题会给出“点×是线段××的中点”这样的条件，那么看到“中点”我们应该想到什么呢？“中点”有哪些作用呢？
已知任意三角形一边上的中点，可以考虑：
倍长中线或类中线（与中点有关的线段）构造全等三角形。
三角形中位线定理。
已知直角三角形斜边中点，可以考虑构造斜边中线。
已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”。
有些题目的中点不直接给出，此时需要我们挖掘题目中隐含中点，例如直角三角形中斜边中点，等腰三角形中底边中点，当没有这些条件的时候，可以用辅助线添加。
【方法精讲】
（1）关于中点中常见的辅助线——“倍长中线（ 型模型）”
中点中常考辅助线——“中位线”
关于直角三角形中的中点常考考点——“斜边中线”
【倍长中线类型练习】
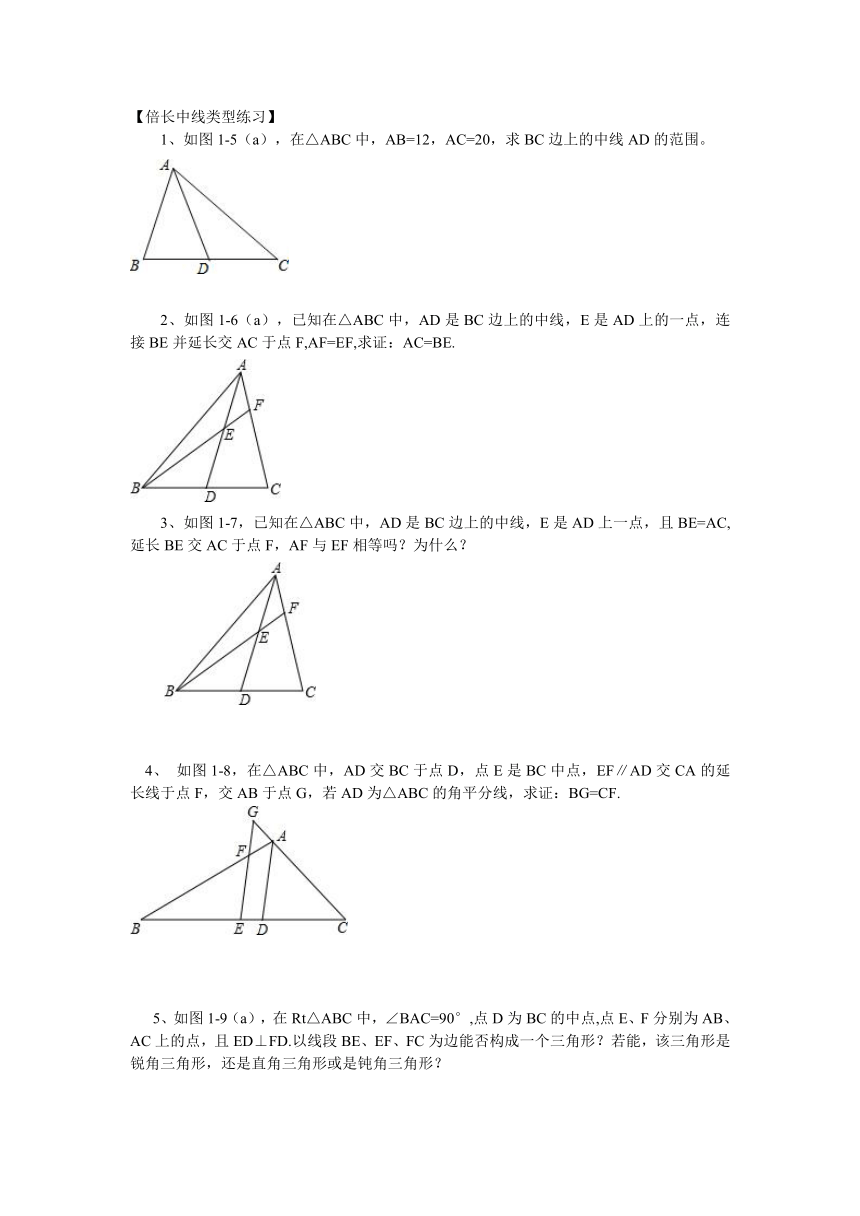
1、如图1-5（a），在△ABC中，AB=12，AC=20，求BC边上的中线AD的范围。

2、如图1-6（a），已知在△ABC中，AD是BC边上的中线，E是AD上的一点，连接BE并延长交AC于点F,AF=EF,求证：AC=BE.

3、如图1-7，已知在△ABC中，AD是BC边上的中线，E是AD上一点，且BE=AC,延长BE交AC于点F，AF与EF相等吗？为什么？

4、 如图1-8，在△ABC中，AD交BC于点D，点E是BC中点，EF∥AD交CA的延长线于点F，交AB于点G，若AD为△ABC的角平分线，求证：BG=CF.

5、如图1-9（a），在Rt△ABC中，∠BAC=90°,点D为BC的中点,点E、F分别为AB、AC上的点，且ED⊥FD.以线段BE、EF、FC为边能否构成一个三角形？若能，该三角形是锐角三角形，还是直角三角形或是钝角三角形？

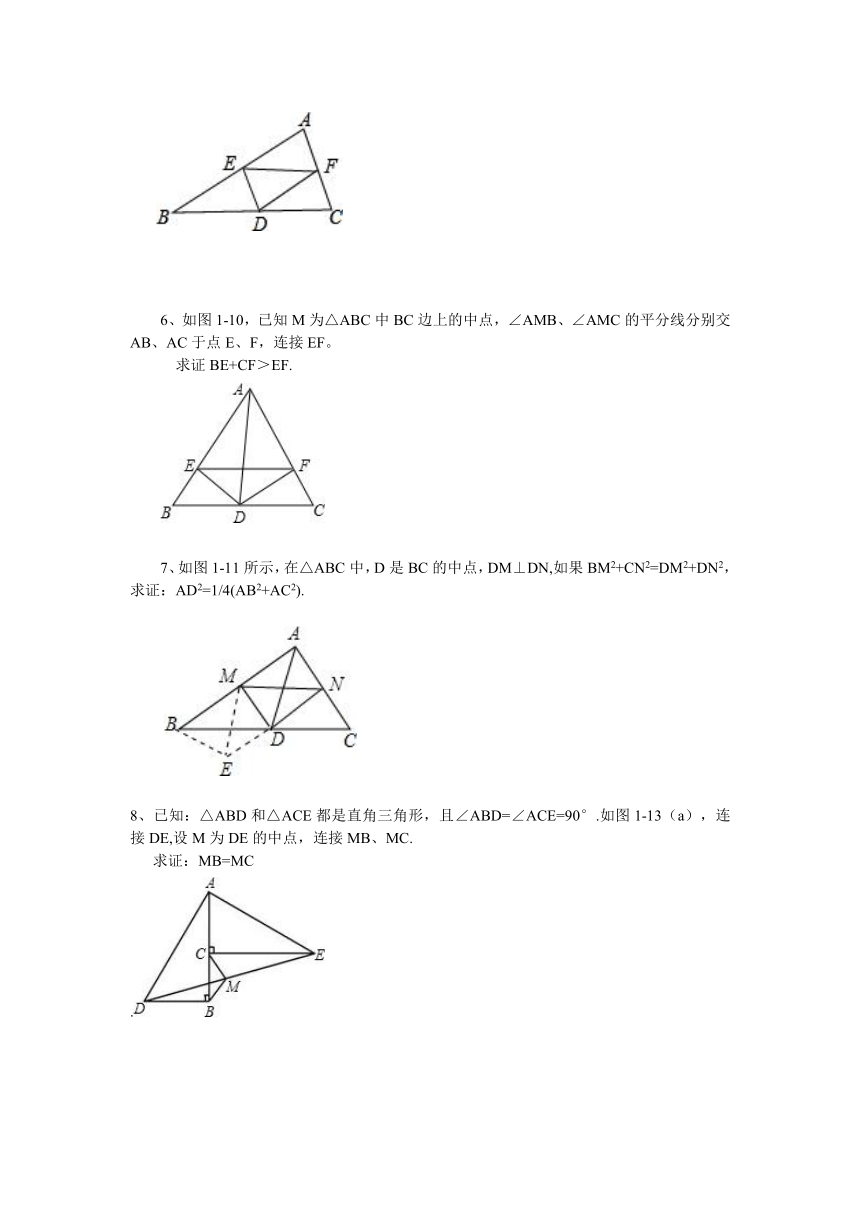
6、如图1-10，已知M为△ABC中BC边上的中点，∠AMB、∠AMC的平分线分别交AB、AC于点E、F，连接EF。
求证BE+CF＞EF.

7、如图1-11所示，在△ABC中，D是BC的中点，DM⊥DN,如果BM2+CN2=DM2+DN2，求证：AD2=1/4(AB2+AC2).

8、已知：△ABD和△ACE都是直角三角形，且∠ABD=∠ACE=90°.如图1-13（a），连接DE,设M为DE的中点，连接MB、MC.
求证：MB=MC
.
【中位线类型练习】
1.小明作出了边长为的第1个正△A1B1C1，算出了正△A1B1C1的面积。然后分别取△A1B1C1的三边中点A2、B2、C2，作出了第2个正△A2B2C2，算出了正△A2B2C2的面积。用同样的方法，作出了第3个正△A3B3C3，算出了正△A3B3C3的面积……，由此可得，第10个正△A10B10C10的面积是（ ）
A． B． C． D．
2、梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC＝5cm，BD＝12cm，求该梯形的中位线长.
3、已知，如图，△ABC的中线BD、CE交于点O，F、G分别是OB、OC的中点。
求证：EF=DG且EF∥DG。
4、如图，在锐角三角形ABC中，AB＜AC，AD⊥BC，交BC与点D，E、F、G分别是BC、CA、AB的中点。求证：四边形DEFG是等腰梯形。
5、如图，在平行四边形ABCD中，E、F分别是BC、AD的中点，AE与BF相交于点G，DE与CF相交于点H，试说明GH∥AD且GH=AD
6、如图，梯形ABCD中，AD∥BC，点E是AB中点，连结EC、ED、CE⊥DE，CD、AD与BC三条线段之间有什么样的数量关系？请说明理由。
7、在△ABC中，AH⊥BC于H，D，E，F分别是BC，CA，AB的中点．
求证：∠DEF=∠HFE．
8、已知，如图梯形ABCD中，AD//BC，对角线AC与BD垂直相交于O，MH是梯形中位线，∠DBC＝30o，猜想MN与AC什么关系？并证明猜想
9、如图，四边形ABCD中，AB=CD，M、N分别是AD、BC的中点，延长BA、NM、CD分别交于点E、F。试说明∠BEN=∠NFC.

10、如图．D，E分别在AB，AC上，BD=CE，BE，CD的中点分别是M，N，直线MN分别交AB，AC于P，Q．求证：AP=AQ．
11、如图，等腰梯形ABCD中，CD∥AB，对角线AC、BD交于O，∠ACD＝60°，点S、P、Q分别是OD、OA、BC的中点。求证：△PQS是等边三角形。