人教版(2019)必修第二册 8.3 动能和动能定理 课件(共24张PPT)
文档属性
| 名称 | 人教版(2019)必修第二册 8.3 动能和动能定理 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1023.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-21 22:27:08 | ||
图片预览







文档简介
(共25张PPT)
8.3 动能和动能定理
物体由于运动而具有的能叫做动能
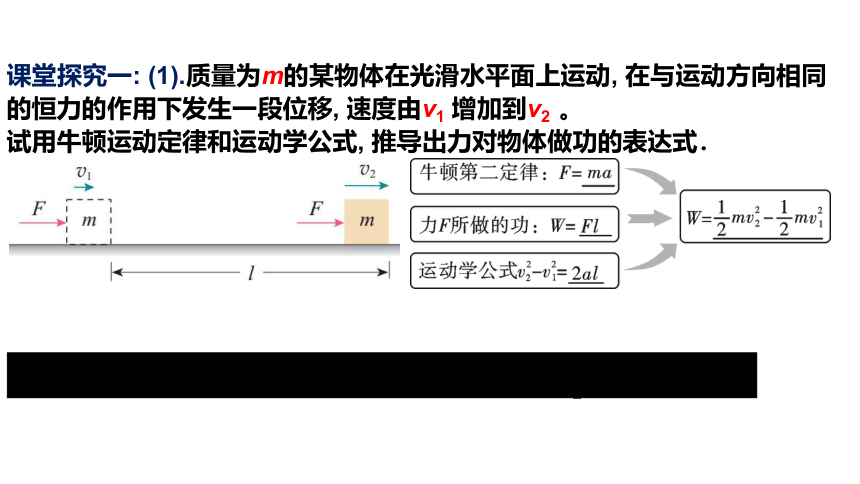
课堂探究一: (1).质量为m的某物体在光滑水平面上运动, 在与运动方向相同的恒力的作用下发生一段位移, 速度由v1 增加到v2 。
试用牛顿运动定律和运动学公式, 推导出力对物体做功的表达式.
(2).请结合动能的特征和力对物体做功的意义, 思考 mv2 的意义?
课堂探究一: (1).质量为m的某物体在光滑水平面上运动, 在与运动方向相同的恒力的作用下发生一段位移, 速度由v1 增加到v2 。
试用牛顿运动定律和运动学公式, 推导出力对物体做功的表达式.
(2).请结合动能的特征和力对物体做功的意义, 思考 mv2 的意义?
(2).请结合动能的特征和力对物体做功的意义, 思考 mv2 的意义?
5.状态量:具有瞬时性
1.定义:物体由于运动而具有的能量叫作动能
2.表达式:
3.单位:焦耳 1kg·m2/s2=1N·m=1J
4.标量:动能总是正值
一、动能的表达式
6.相对性:因为速度具有相对性, 通常是相对于地面的速度
Ek = mv2
练习1、关于动能的理解,下列说法正确的是( )
A.动能是普遍存在的机械能的一种基本形式,运动物体都具有动能
B. ,v一般指物体相对于地面的速度,且动能总是正值
C.一定质量的物体,动能变化时,速度一定变化,但速度变化时,动能不一定变化
D.动能不变的物体,一定处于平衡状态
(一)动能的表达式
ABC
5.状态量:具有瞬时性
1.定义:物体由于运动而具有的能量叫作动能
2.表达式:
3.单位:焦耳 1kg·m2/s2=1N·m=1J
4.标量:动能总是正值
一、动能的表达式
6.相对性:因为速度具有相对性, 通常是相对于地面的速度
(4). 思考:动能与速度的关系
①速度具有方向, 那么动能的大小与速度的方向有关吗
②质量一定, 速度变化时动能一定改变吗
③质量一定, 动能变化时速度一定改变吗
④匀速圆周运动的动能变化吗
Ek = mv2
5.状态量:具有瞬时性
1.定义:物体由于运动而具有的能量叫作动能
2.表达式:
3.单位:焦耳 1kg·m2/s2=1N·m=1J
4.标量:动能总是正值
一、动能的表达式
6.相对性:因为速度具有相对性, 通常是相对于地面的速度
7.与速度关系:
(1)数值关系:Ek=mv2, 质量一定时, 速度v越大, 动能Ek越大.
(2)瞬时关系:动能和速度均为状态量,二者具有瞬时对应关系.
(3)变化关系:动能是标量, 速度是矢量,
质量一定的物体动能变化时速度(大小)一定变化;
速度变化时可能仅是速度方向变化, 物体的动能可能不变
Ek = mv2
如图小球碰墙后以原速率反弹 ,
小球的速度和动能都变化了吗
W合 = mv22 mv12
2. 表达式:
1. 内容:
或 W合 = Ek2 Ek1
合外力对物体所做的总功等于物体动能的变化量
二、动能定理
思考: 动能定理是矢量式还是标量式
W合 = mv22 mv12
2. 表达式:
1. 内容:
或 W合 = Ek2 Ek1
力在一个过程中对物体做的功,
等于物体在这个过程中动能的变化.
即:合外力对物体所做的总功等于物体动能的变化量
二、动能定理
合外力做的总功
①.W合= F合l cosθ
②.W合=W1+W2 +…
末动能
初动能
等号的含义
①数量关系: 合外力做的总功与物体动能的变化量相等
②单位关系: 国际单位都是焦耳
③因果关系: 合力做功是物体动能变化的原因
二、动能定理
动能定理的适用范围
(1) 恒力做功或变力做功;
(2) 直线运动或曲线运动;
动能定理的说明
(1) 合力做正功,物体的动能增加;
(2) 合力做负功,物体的动能减少。
巩固训练
一架喷气式飞机,质量m为7.0×104kg,起飞过程中从静止开始滑跑。当位移l达到2.5×103m时,速度达到起飞速度80m/s。此过程中,飞机受到的平均阻力是飞机所受重力的 。g取10 m/s2,求飞机平均牵引力的大小。
例题1:
物体从高出地面H处由静止自由落下,不考虑空气阻力,落至地面掉入沙坑h处停止,如图所示,求物体在沙坑中受到的平均阻力F 是其重力的多少倍
解一:对全过程,由动能定理得:
解得:
解二:设物体落到地面时速度为v,从静止下落到地面,由动能定理得:
解得:
由地面掉入沙坑h 处,由动能定理得:
例题2:
.我们曾在第四章中用牛顿运动定律解答过一个问题:民航客机机舱紧急出口的气囊是一条连接出口与底面的斜面,若斜面高3.2m,斜面长6.5m,质量为60的人沿斜面滑下时所受的阻力是240N,求人滑至底端时的速度大小,g取10。
解:对人从出口→底端, 由动能定理:
mgh-f l = mv2 - 0
得 v =
左边写合外力做功
右边写动能变化量
例题3:
如图所示,质量m=1 kg的物体从轨道上的A点由静止下滑,轨道AB是弯曲的,且A点高出B 点h=0.8m.物体到达B点时的速度为2 m/s,求物体在A→B 过程中克服摩擦力所做的功.
解:物体在A→B 过程,设摩擦力做功 Wf,由动能定理得:
解得:
克服摩擦力所做的功:
注意:1、是求“克服某力做功”;
2、变力做功则用“W+下标”表示
例题4:
如图所示,物体在离斜面底端 4m 处由静止滑下,若动摩擦因数均为0.5,斜面倾角为37°,斜面与平面间由一小段圆弧连接,求物体能在水平面上滑行多远.
解:由静止滑下到停下的过程,由动能定理得:
解得:
分析:
在斜面上:
摩擦力做功
重力做功
在水平面上:
例题5:
如图所示,AB为四分之一圆弧轨道,BC为水平直轨道,圆弧半径为R,BC长度为R。一质量为m的物体,与两个轨道的动摩擦因数都为μ,当它由轨道顶端A从静止下滑时,恰好运动到C处停止,求:物体在AB段克服摩擦力做的功;
分析:
在圆弧轨道AB上:
设AB段摩擦力做功为
重力做功
在水平轨道上:
则克服摩擦力做功为
BC段摩擦力做功为
总功为各个力做功的代数和:
初末状态动能变化为0
例题6:
.一人用力把质量为1 kg的物体由静止提高1 m,使物体获得2 m/s的速度(g=10 m/s2),下列说法错误的是( )
A.人对物体做的功为12 J
B.物体动能增加2 J
C.合外力对物体做的功为12 J
D.物体重力势能增加10 J
例题7:
【答案】C
.一质量为m 的小球,用长为l 的轻绳悬挂于O点.小球在水平力F 作用下,从平衡位置P 点很缓慢地移动到Q 点,如图所示,则力F 所做的功为
A.mglcos θ B.Flsin θ
C.mgl(1-cos θ) D.Flcos θ
F
mg
θ
T
缓慢地移动:合力为零,速度不变
对求受力分析如图:
所以F是变力
变力做功,优先用动能定理
分析:
例题8:
小结
1.定义:物体由于运动而具有的能,叫动能
2.公式:
3.动能是标量,是状态量
4.单位:焦(J)
1.内容:合外力所做的功等于物体动能的变化
2.表达式:
3.解题步骤:
(1)定对象,选过程;
(2)析受力,算总功;
(3)知运动,定初末;
(4)列方程,细求解。
í
ì
í
ì
í
ì
动能定理
动能
动能
动能定理
9.如图所示是游乐场中过山车抽象的理想化模型(圆形轨道与斜轨道之间平滑连接,不计摩擦和空气阻力).已知圆轨道的半径为R,质量为m 的小车(视作质点)从P点由静止沿斜轨道下滑,进入圆轨道后沿圆轨道运动.已知P点到圆轨道最低点B的高度差H=3R,求:
(1)小车到达B点时的速度大小;
(2)小车在A 点受到的压力大小.
1、分过程:
A 点为圆周运动最高点,用圆周运动知识
计算题解题关键:
2、找特殊的位置:
①由P到B ,由B到A两个小过程;
②由P到B,由P到A等两个过程;
如圆周最高点A、最低点B
出现初末速度优先用动能定理
解:小车由静止下滑到B,由动能定理得:
解得:
小车在A 点受力分析如图,由牛顿第二定律得:
mg
F
小车由B到A,由动能定理得:
由上述各式解得:
10.如图所示,竖直平面内的 圆弧形光滑管道半径略大于小球半径,管道中心到圆心距离为R,A端与圆心O 等高,AD为水平面,B 端在O 的正下方,小球自A点正上方由静止释放,自由下落至A点进入管道,当小球到达B点时,管壁对小球的弹力大小为小球重力的9倍。求:
(1)释放点距 A 的竖直高度;
(2)落点 C 与 A 水平距离。
分析:
2、①由静止下落至B点,出现初末速度,优先用动能定理;
3、最后做平抛运动,用平抛运动的知识
1、B点是圆周运动最低点,用圆周运动在最低点的知识
②由B点至管顶,出现初末速度,优先用动能定理;
解:(1)小球在B点受力分析如图,由牛顿第二定律得:
小球由静止下落至B点,由动能定理得:
由①②解得:
①
②
(2)设小球到达最点的速度为v2 ,小球由B点至最高点过程,由动能定理得:
从最高点落到C 做平抛运动,则:
④
⑤
③
落点C 与A的水平距离:
⑥
由上述各式解得:
小结
1.定义:物体由于运动而具有的能,叫动能
2.公式:
3.动能是标量,是状态量
4.单位:焦(J)
1.内容:合外力所做的功等于物体动能的变化
2.表达式:
3.解题步骤:
(1)定对象,选过程;
(2)析受力,算总功;
(3)知运动,定初末;
(4)列方程,细求解。
í
ì
í
ì
í
ì
动能定理
动能
动能
动能定理
8.3 动能和动能定理
物体由于运动而具有的能叫做动能
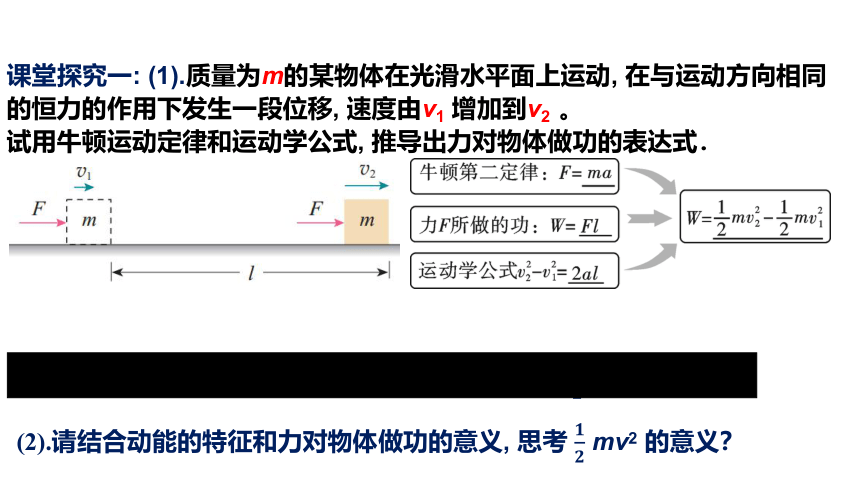
课堂探究一: (1).质量为m的某物体在光滑水平面上运动, 在与运动方向相同的恒力的作用下发生一段位移, 速度由v1 增加到v2 。
试用牛顿运动定律和运动学公式, 推导出力对物体做功的表达式.
(2).请结合动能的特征和力对物体做功的意义, 思考 mv2 的意义?
课堂探究一: (1).质量为m的某物体在光滑水平面上运动, 在与运动方向相同的恒力的作用下发生一段位移, 速度由v1 增加到v2 。
试用牛顿运动定律和运动学公式, 推导出力对物体做功的表达式.
(2).请结合动能的特征和力对物体做功的意义, 思考 mv2 的意义?
(2).请结合动能的特征和力对物体做功的意义, 思考 mv2 的意义?
5.状态量:具有瞬时性
1.定义:物体由于运动而具有的能量叫作动能
2.表达式:
3.单位:焦耳 1kg·m2/s2=1N·m=1J
4.标量:动能总是正值
一、动能的表达式
6.相对性:因为速度具有相对性, 通常是相对于地面的速度
Ek = mv2
练习1、关于动能的理解,下列说法正确的是( )
A.动能是普遍存在的机械能的一种基本形式,运动物体都具有动能
B. ,v一般指物体相对于地面的速度,且动能总是正值
C.一定质量的物体,动能变化时,速度一定变化,但速度变化时,动能不一定变化
D.动能不变的物体,一定处于平衡状态
(一)动能的表达式
ABC
5.状态量:具有瞬时性
1.定义:物体由于运动而具有的能量叫作动能
2.表达式:
3.单位:焦耳 1kg·m2/s2=1N·m=1J
4.标量:动能总是正值
一、动能的表达式
6.相对性:因为速度具有相对性, 通常是相对于地面的速度
(4). 思考:动能与速度的关系
①速度具有方向, 那么动能的大小与速度的方向有关吗
②质量一定, 速度变化时动能一定改变吗
③质量一定, 动能变化时速度一定改变吗
④匀速圆周运动的动能变化吗
Ek = mv2
5.状态量:具有瞬时性
1.定义:物体由于运动而具有的能量叫作动能
2.表达式:
3.单位:焦耳 1kg·m2/s2=1N·m=1J
4.标量:动能总是正值
一、动能的表达式
6.相对性:因为速度具有相对性, 通常是相对于地面的速度
7.与速度关系:
(1)数值关系:Ek=mv2, 质量一定时, 速度v越大, 动能Ek越大.
(2)瞬时关系:动能和速度均为状态量,二者具有瞬时对应关系.
(3)变化关系:动能是标量, 速度是矢量,
质量一定的物体动能变化时速度(大小)一定变化;
速度变化时可能仅是速度方向变化, 物体的动能可能不变
Ek = mv2
如图小球碰墙后以原速率反弹 ,
小球的速度和动能都变化了吗
W合 = mv22 mv12
2. 表达式:
1. 内容:
或 W合 = Ek2 Ek1
合外力对物体所做的总功等于物体动能的变化量
二、动能定理
思考: 动能定理是矢量式还是标量式
W合 = mv22 mv12
2. 表达式:
1. 内容:
或 W合 = Ek2 Ek1
力在一个过程中对物体做的功,
等于物体在这个过程中动能的变化.
即:合外力对物体所做的总功等于物体动能的变化量
二、动能定理
合外力做的总功
①.W合= F合l cosθ
②.W合=W1+W2 +…
末动能
初动能
等号的含义
①数量关系: 合外力做的总功与物体动能的变化量相等
②单位关系: 国际单位都是焦耳
③因果关系: 合力做功是物体动能变化的原因
二、动能定理
动能定理的适用范围
(1) 恒力做功或变力做功;
(2) 直线运动或曲线运动;
动能定理的说明
(1) 合力做正功,物体的动能增加;
(2) 合力做负功,物体的动能减少。
巩固训练
一架喷气式飞机,质量m为7.0×104kg,起飞过程中从静止开始滑跑。当位移l达到2.5×103m时,速度达到起飞速度80m/s。此过程中,飞机受到的平均阻力是飞机所受重力的 。g取10 m/s2,求飞机平均牵引力的大小。
例题1:
物体从高出地面H处由静止自由落下,不考虑空气阻力,落至地面掉入沙坑h处停止,如图所示,求物体在沙坑中受到的平均阻力F 是其重力的多少倍
解一:对全过程,由动能定理得:
解得:
解二:设物体落到地面时速度为v,从静止下落到地面,由动能定理得:
解得:
由地面掉入沙坑h 处,由动能定理得:
例题2:
.我们曾在第四章中用牛顿运动定律解答过一个问题:民航客机机舱紧急出口的气囊是一条连接出口与底面的斜面,若斜面高3.2m,斜面长6.5m,质量为60的人沿斜面滑下时所受的阻力是240N,求人滑至底端时的速度大小,g取10。
解:对人从出口→底端, 由动能定理:
mgh-f l = mv2 - 0
得 v =
左边写合外力做功
右边写动能变化量
例题3:
如图所示,质量m=1 kg的物体从轨道上的A点由静止下滑,轨道AB是弯曲的,且A点高出B 点h=0.8m.物体到达B点时的速度为2 m/s,求物体在A→B 过程中克服摩擦力所做的功.
解:物体在A→B 过程,设摩擦力做功 Wf,由动能定理得:
解得:
克服摩擦力所做的功:
注意:1、是求“克服某力做功”;
2、变力做功则用“W+下标”表示
例题4:
如图所示,物体在离斜面底端 4m 处由静止滑下,若动摩擦因数均为0.5,斜面倾角为37°,斜面与平面间由一小段圆弧连接,求物体能在水平面上滑行多远.
解:由静止滑下到停下的过程,由动能定理得:
解得:
分析:
在斜面上:
摩擦力做功
重力做功
在水平面上:
例题5:
如图所示,AB为四分之一圆弧轨道,BC为水平直轨道,圆弧半径为R,BC长度为R。一质量为m的物体,与两个轨道的动摩擦因数都为μ,当它由轨道顶端A从静止下滑时,恰好运动到C处停止,求:物体在AB段克服摩擦力做的功;
分析:
在圆弧轨道AB上:
设AB段摩擦力做功为
重力做功
在水平轨道上:
则克服摩擦力做功为
BC段摩擦力做功为
总功为各个力做功的代数和:
初末状态动能变化为0
例题6:
.一人用力把质量为1 kg的物体由静止提高1 m,使物体获得2 m/s的速度(g=10 m/s2),下列说法错误的是( )
A.人对物体做的功为12 J
B.物体动能增加2 J
C.合外力对物体做的功为12 J
D.物体重力势能增加10 J
例题7:
【答案】C
.一质量为m 的小球,用长为l 的轻绳悬挂于O点.小球在水平力F 作用下,从平衡位置P 点很缓慢地移动到Q 点,如图所示,则力F 所做的功为
A.mglcos θ B.Flsin θ
C.mgl(1-cos θ) D.Flcos θ
F
mg
θ
T
缓慢地移动:合力为零,速度不变
对求受力分析如图:
所以F是变力
变力做功,优先用动能定理
分析:
例题8:
小结
1.定义:物体由于运动而具有的能,叫动能
2.公式:
3.动能是标量,是状态量
4.单位:焦(J)
1.内容:合外力所做的功等于物体动能的变化
2.表达式:
3.解题步骤:
(1)定对象,选过程;
(2)析受力,算总功;
(3)知运动,定初末;
(4)列方程,细求解。
í
ì
í
ì
í
ì
动能定理
动能
动能
动能定理
9.如图所示是游乐场中过山车抽象的理想化模型(圆形轨道与斜轨道之间平滑连接,不计摩擦和空气阻力).已知圆轨道的半径为R,质量为m 的小车(视作质点)从P点由静止沿斜轨道下滑,进入圆轨道后沿圆轨道运动.已知P点到圆轨道最低点B的高度差H=3R,求:
(1)小车到达B点时的速度大小;
(2)小车在A 点受到的压力大小.
1、分过程:
A 点为圆周运动最高点,用圆周运动知识
计算题解题关键:
2、找特殊的位置:
①由P到B ,由B到A两个小过程;
②由P到B,由P到A等两个过程;
如圆周最高点A、最低点B
出现初末速度优先用动能定理
解:小车由静止下滑到B,由动能定理得:
解得:
小车在A 点受力分析如图,由牛顿第二定律得:
mg
F
小车由B到A,由动能定理得:
由上述各式解得:
10.如图所示,竖直平面内的 圆弧形光滑管道半径略大于小球半径,管道中心到圆心距离为R,A端与圆心O 等高,AD为水平面,B 端在O 的正下方,小球自A点正上方由静止释放,自由下落至A点进入管道,当小球到达B点时,管壁对小球的弹力大小为小球重力的9倍。求:
(1)释放点距 A 的竖直高度;
(2)落点 C 与 A 水平距离。
分析:
2、①由静止下落至B点,出现初末速度,优先用动能定理;
3、最后做平抛运动,用平抛运动的知识
1、B点是圆周运动最低点,用圆周运动在最低点的知识
②由B点至管顶,出现初末速度,优先用动能定理;
解:(1)小球在B点受力分析如图,由牛顿第二定律得:
小球由静止下落至B点,由动能定理得:
由①②解得:
①
②
(2)设小球到达最点的速度为v2 ,小球由B点至最高点过程,由动能定理得:
从最高点落到C 做平抛运动,则:
④
⑤
③
落点C 与A的水平距离:
⑥
由上述各式解得:
小结
1.定义:物体由于运动而具有的能,叫动能
2.公式:
3.动能是标量,是状态量
4.单位:焦(J)
1.内容:合外力所做的功等于物体动能的变化
2.表达式:
3.解题步骤:
(1)定对象,选过程;
(2)析受力,算总功;
(3)知运动,定初末;
(4)列方程,细求解。
í
ì
í
ì
í
ì
动能定理
动能
动能
动能定理
