2023年安徽中考数学押题预测卷(含答案)
文档属性
| 名称 | 2023年安徽中考数学押题预测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 972.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 06:37:26 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023年安徽中考数学押题预测卷
数 学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
A卷
第Ⅰ卷
一、单选题
1.在中,无理数有( )
A.个 B.个 C.个 D.个
2.地球绕太阳每小时转动通过的路程约是,用科学记数法表示地球一天(以24小时计)转动通过的路程约是( )
A. B. C. D.
3.一个几何体的三视图如下:其中主视图都是腰长为4、底边为2的等腰三角形,则这个几何体的侧面展开图的面积为( )
A. B. C. D.
4.如图,是关于x的不等式2x-a≤﹣1的解集,则a的值为( )
A.a=﹣2 B.a=﹣1 C.a≤﹣2 D.a≤﹣1
5.已知则代数式的值为( )
A.2021 B.2021 C.2019 D.2019
6.如图,在一块正三角形飞镖游戏板上画一个正六边形(图中阴影部分),假设飞镖投中游戏板上的每一点是等可能的(若投中边界或没有投中游戏板,则重投1次),任意投掷飞镖1次,则飞镖投中阴影部分的概率为( )
A. B. C. D.
7.对于一次函数,下列说法正确的是( )
A.图像不经过第二象限 B.随的增大而增大
C.图像与两坐标轴围成的三角形的面积为4 D.该函数图像的与y轴的交点坐标为(0,-2)
8.若关于x的分式方程 = 的根为正数,则k的取值范围是( )
A.k<- 且k≠-1 B.k≠-1 C.-9.如图,在矩形中,为边上一点,连接,过点作于,若,,则的长为( )
A. B. C.1 D.2
10.点M为正方形的边的中点,分别连接交的延长线于E,于F,交于G.设和的面积分别为、、和,则下列结论错误的是( )
A. B.
C. D.
第Ⅱ卷
二、填空题
11.把 中根号外面的因式移到根号内的结果是___.
12.因式分解:______.
13.若,,是反比例函数图象上的点,且,则、、的大小关系是__________.
14.如图,正方形ABCD内有一等边三角形BCE,直线DE交AB于点H,过点E作直线GF⊥DH交BC于点G,交AD于点F.以下结论:①∠CEG=15°;②AF=DF;③BH=3AH;④BE=HE+GE;正确的有_________.(填序号)
三、解答题
15.计算:
16.已知关于x,y的方程组的解满足,求k的值.
17.如图,在由边长为个单位长度的小正方形组成的网格中,给出了格点.
(1)将绕格点顺时针旋转,得到,画出;
(2)尺规作图:过格点作的垂线,标出垂足(保留作图痕迹,不写作法);
(3)求线段的长.
18.观察以下等式:
第1个等式:,
第2个等式:,
第3个等式:,
第4个等式:,……
按照以上规律,解决下列问题:
(1)写出第5个等式:__________;
(2)写出你猜想的第个等式(用含的等式表示),并证明.
19.如图,已知为的直径,过上点的切线交的延长线于点,于点.且交于点,连接,,.
(1)求证:;
(2)若,,求的长.
20.某工程队计划测量一信号塔OC的高度,由于特殊原因无法直接到达信号塔OC底部,因此计划借助坡面高度来测量信号塔OC的高度;如图,在信号塔OC旁山坡坡脚A处测得信号塔OC顶端C的仰角为70°,当从A处沿坡面行走13米到达P处时,测得信号塔OC顶端C的仰角刚好为45°.已知山坡的坡度i=1:2.4,且O,A,B在同一直线上.
(1)求点P到水平地面OB的距离.
(2)求信号塔OC的高度.(侧倾器高度忽略不计,结果精确到0.1米,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.7.)
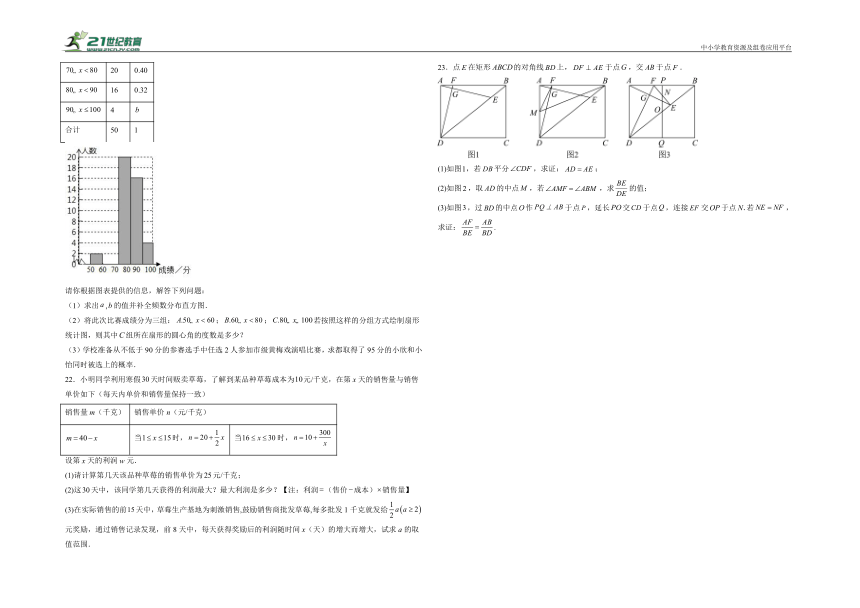
21.某中学开展黄梅戏演唱比赛,组委会将本次比赛的成绩(单位:分)进行整理,并绘制成如下频数分布表和频数分布直方图(不完整).
成绩 频数 频率
2 0.04
0.16
20 0.40
16 0.32
4
合计 50 1
请你根据图表提供的信息,解答下列问题:
(1)求出,的值并补全频数分布直方图.
(2)将此次比赛成绩分为三组:;;若按照这样的分组方式绘制扇形统计图,则其中组所在扇形的圆心角的度数是多少?
(3)学校准备从不低于90分的参赛选手中任选2人参加市级黄梅戏演唱比赛,求都取得了95分的小欣和小怡同时被选上的概率.
22.小明同学利用寒假天时间贩卖草莓,了解到某品种草莓成本为元/千克,在第x天的销售量与销售单价如下(每天内单价和销售量保持一致)
销售量m(千克) 销售单价n(元/千克)
当时, 当时,
设第x天的利润w元.
(1)请计算第几天该品种草莓的销售单价为元/千克;
(2)这天中,该同学第几天获得的利润最大?最大利润是多少?【注:利润(售价成本)销售量】
(3)在实际销售的前天中,草莓生产基地为刺激销售,鼓励销售商批发草莓,每多批发1千克就发给元奖励,通过销售记录发现,前8天中,每天获得奖励后的利润随时间x(天)的增大而增大,试求a的取值范围.
23.点在矩形的对角线上,于点,交于点.
(1)如图,若平分,求证:;
(2)如图,取的中点,若,求的值;
(3)如图,过的中点作于点,延长交于点,连接交于点若,求证:.
参考答案
第Ⅰ卷
一、选择题
1.A 2.B 3.C 4.B 5.C 6.D 7.D 8.A 9.C 10.D
二、填空题
11.
12.
13.
14.①
三、解答题
15.
【详解】解:
16.
【详解】解:,得,
∴,
∴,
∴,
∴,
解得.
17.(1)如图所示,见解析;(2)如图所示,见解析;(3).
【详解】(1)如图所示,
(2)如图所示,
(3) S△ABC==8
AB=
∴CD==.
18.(1)
(2);证明见解析
【详解】(1)解:由已知等式可知:等式左边括号外分数的分子为等式的序号加1,分母为序号加2,括号内分数的分母为序号加1;等式右边为1,
∴第5个等式:;
故答案为:;
(2)解:由(1)猜想第个等式为;证明如下:
∵左边右边,
∴等式成立.
19.(1)见解析
(2)
【详解】(1)解:证明:如图,连接,
切于点,
,
,
,
,
,
,
,
;
(2)在中,
,,
∴,
,
,
,
设的半径为,
,
,
,
,
答:的长为.
20.(1)5米
(2)米
(1)解:如图,过点P作PE⊥OB于点E,PF⊥OC于点F,
∵i=1:2.4,,∴,∴设PE=5x,则AE=12x,在Rt△AEP中,由勾股定理得:(5x)2+(12x)2=132,解得:或(舍去),∴PE=5,则AE=12,∴点P到水平地面OB的距离为5米.
(2)解:∵∠CPF=∠PCF= 45°,∴,设CF=PF=m米,则OC= (m+5) 米,OA=(m-12)米,在Rt△AOC中,,即:,解得:,∴(米)∴信号塔OC的高度约为米.
21.(1)a=8,b=0.08;补图见解析;(2)144°;(3).
【详解】(1),.
补全频数分布直方图如下:
(2).
故C组所在扇形的圆心角的度数为.
(3)由题意知,不低于90分的学生共有4人,设这四名学生分别为,,,,其中小欣和小怡分别用,表示,根据题意,画树状图如下.
由树状图可知,共有12种等可能的结果,其中小欣和小怡同时被选上的结果有2种,故小欣和小怡同时被选上的概率是.
22.(1)第天或第天该品种草莓的销售单价为元/千克
(2)第天或第天获得的利润最大,最大利润均为元
(3)
【详解】(1)解:当时,把代入,
得,
解得,
当时,把代入,
得,
解得,
经检验是原方程的解,且符合题意,
答:第天或第天该品种草莓的销售单价为元/千克;
(2)解:当时,,
,
当时,有最大值为元;
当时,,
,当时,随x的增大而减小,
当时,有最大值为元,
答:第天或第天获得的利润最大,最大利润均为元;
(3)解:
,
前8天中,每天获得奖励后的利润随时间x(天)的增大而增大,,
该抛物线的对称轴为直线,
解得,
又,
的取值范围为.
23.(1)证明见解析
(2)
(3)证明见解析
【详解】(1)证明:四边形是矩形,
,,
,
,
,
,
,
,
平分,
,
,
,
.
(2)解:,,
,
①,
如图2,作于,
,,
,
又是中点,
②,
由(1)可知,,
,
③,
由①②③得:,即,
又,
.
(3)证明:如图,连接,
矩形中,是对角线的中点,
,
,
(等腰三角形的三线合一),
作于,则,,
,
,
,
,即,
又,
,
,
.
模拟考试 第3页(共6页) 模拟考试 第4页(共6页)
2023年安徽中考数学押题预测卷
数 学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
A卷
第Ⅰ卷
一、单选题
1.在中,无理数有( )
A.个 B.个 C.个 D.个
2.地球绕太阳每小时转动通过的路程约是,用科学记数法表示地球一天(以24小时计)转动通过的路程约是( )
A. B. C. D.
3.一个几何体的三视图如下:其中主视图都是腰长为4、底边为2的等腰三角形,则这个几何体的侧面展开图的面积为( )
A. B. C. D.
4.如图,是关于x的不等式2x-a≤﹣1的解集,则a的值为( )
A.a=﹣2 B.a=﹣1 C.a≤﹣2 D.a≤﹣1
5.已知则代数式的值为( )
A.2021 B.2021 C.2019 D.2019
6.如图,在一块正三角形飞镖游戏板上画一个正六边形(图中阴影部分),假设飞镖投中游戏板上的每一点是等可能的(若投中边界或没有投中游戏板,则重投1次),任意投掷飞镖1次,则飞镖投中阴影部分的概率为( )
A. B. C. D.
7.对于一次函数,下列说法正确的是( )
A.图像不经过第二象限 B.随的增大而增大
C.图像与两坐标轴围成的三角形的面积为4 D.该函数图像的与y轴的交点坐标为(0,-2)
8.若关于x的分式方程 = 的根为正数,则k的取值范围是( )
A.k<- 且k≠-1 B.k≠-1 C.-
A. B. C.1 D.2
10.点M为正方形的边的中点,分别连接交的延长线于E,于F,交于G.设和的面积分别为、、和,则下列结论错误的是( )
A. B.
C. D.
第Ⅱ卷
二、填空题
11.把 中根号外面的因式移到根号内的结果是___.
12.因式分解:______.
13.若,,是反比例函数图象上的点,且,则、、的大小关系是__________.
14.如图,正方形ABCD内有一等边三角形BCE,直线DE交AB于点H,过点E作直线GF⊥DH交BC于点G,交AD于点F.以下结论:①∠CEG=15°;②AF=DF;③BH=3AH;④BE=HE+GE;正确的有_________.(填序号)
三、解答题
15.计算:
16.已知关于x,y的方程组的解满足,求k的值.
17.如图,在由边长为个单位长度的小正方形组成的网格中,给出了格点.
(1)将绕格点顺时针旋转,得到,画出;
(2)尺规作图:过格点作的垂线,标出垂足(保留作图痕迹,不写作法);
(3)求线段的长.
18.观察以下等式:
第1个等式:,
第2个等式:,
第3个等式:,
第4个等式:,……
按照以上规律,解决下列问题:
(1)写出第5个等式:__________;
(2)写出你猜想的第个等式(用含的等式表示),并证明.
19.如图,已知为的直径,过上点的切线交的延长线于点,于点.且交于点,连接,,.
(1)求证:;
(2)若,,求的长.
20.某工程队计划测量一信号塔OC的高度,由于特殊原因无法直接到达信号塔OC底部,因此计划借助坡面高度来测量信号塔OC的高度;如图,在信号塔OC旁山坡坡脚A处测得信号塔OC顶端C的仰角为70°,当从A处沿坡面行走13米到达P处时,测得信号塔OC顶端C的仰角刚好为45°.已知山坡的坡度i=1:2.4,且O,A,B在同一直线上.
(1)求点P到水平地面OB的距离.
(2)求信号塔OC的高度.(侧倾器高度忽略不计,结果精确到0.1米,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.7.)
21.某中学开展黄梅戏演唱比赛,组委会将本次比赛的成绩(单位:分)进行整理,并绘制成如下频数分布表和频数分布直方图(不完整).
成绩 频数 频率
2 0.04
0.16
20 0.40
16 0.32
4
合计 50 1
请你根据图表提供的信息,解答下列问题:
(1)求出,的值并补全频数分布直方图.
(2)将此次比赛成绩分为三组:;;若按照这样的分组方式绘制扇形统计图,则其中组所在扇形的圆心角的度数是多少?
(3)学校准备从不低于90分的参赛选手中任选2人参加市级黄梅戏演唱比赛,求都取得了95分的小欣和小怡同时被选上的概率.
22.小明同学利用寒假天时间贩卖草莓,了解到某品种草莓成本为元/千克,在第x天的销售量与销售单价如下(每天内单价和销售量保持一致)
销售量m(千克) 销售单价n(元/千克)
当时, 当时,
设第x天的利润w元.
(1)请计算第几天该品种草莓的销售单价为元/千克;
(2)这天中,该同学第几天获得的利润最大?最大利润是多少?【注:利润(售价成本)销售量】
(3)在实际销售的前天中,草莓生产基地为刺激销售,鼓励销售商批发草莓,每多批发1千克就发给元奖励,通过销售记录发现,前8天中,每天获得奖励后的利润随时间x(天)的增大而增大,试求a的取值范围.
23.点在矩形的对角线上,于点,交于点.
(1)如图,若平分,求证:;
(2)如图,取的中点,若,求的值;
(3)如图,过的中点作于点,延长交于点,连接交于点若,求证:.
参考答案
第Ⅰ卷
一、选择题
1.A 2.B 3.C 4.B 5.C 6.D 7.D 8.A 9.C 10.D
二、填空题
11.
12.
13.
14.①
三、解答题
15.
【详解】解:
16.
【详解】解:,得,
∴,
∴,
∴,
∴,
解得.
17.(1)如图所示,见解析;(2)如图所示,见解析;(3).
【详解】(1)如图所示,
(2)如图所示,
(3) S△ABC==8
AB=
∴CD==.
18.(1)
(2);证明见解析
【详解】(1)解:由已知等式可知:等式左边括号外分数的分子为等式的序号加1,分母为序号加2,括号内分数的分母为序号加1;等式右边为1,
∴第5个等式:;
故答案为:;
(2)解:由(1)猜想第个等式为;证明如下:
∵左边右边,
∴等式成立.
19.(1)见解析
(2)
【详解】(1)解:证明:如图,连接,
切于点,
,
,
,
,
,
,
,
;
(2)在中,
,,
∴,
,
,
,
设的半径为,
,
,
,
,
答:的长为.
20.(1)5米
(2)米
(1)解:如图,过点P作PE⊥OB于点E,PF⊥OC于点F,
∵i=1:2.4,,∴,∴设PE=5x,则AE=12x,在Rt△AEP中,由勾股定理得:(5x)2+(12x)2=132,解得:或(舍去),∴PE=5,则AE=12,∴点P到水平地面OB的距离为5米.
(2)解:∵∠CPF=∠PCF= 45°,∴,设CF=PF=m米,则OC= (m+5) 米,OA=(m-12)米,在Rt△AOC中,,即:,解得:,∴(米)∴信号塔OC的高度约为米.
21.(1)a=8,b=0.08;补图见解析;(2)144°;(3).
【详解】(1),.
补全频数分布直方图如下:
(2).
故C组所在扇形的圆心角的度数为.
(3)由题意知,不低于90分的学生共有4人,设这四名学生分别为,,,,其中小欣和小怡分别用,表示,根据题意,画树状图如下.
由树状图可知,共有12种等可能的结果,其中小欣和小怡同时被选上的结果有2种,故小欣和小怡同时被选上的概率是.
22.(1)第天或第天该品种草莓的销售单价为元/千克
(2)第天或第天获得的利润最大,最大利润均为元
(3)
【详解】(1)解:当时,把代入,
得,
解得,
当时,把代入,
得,
解得,
经检验是原方程的解,且符合题意,
答:第天或第天该品种草莓的销售单价为元/千克;
(2)解:当时,,
,
当时,有最大值为元;
当时,,
,当时,随x的增大而减小,
当时,有最大值为元,
答:第天或第天获得的利润最大,最大利润均为元;
(3)解:
,
前8天中,每天获得奖励后的利润随时间x(天)的增大而增大,,
该抛物线的对称轴为直线,
解得,
又,
的取值范围为.
23.(1)证明见解析
(2)
(3)证明见解析
【详解】(1)证明:四边形是矩形,
,,
,
,
,
,
,
,
平分,
,
,
,
.
(2)解:,,
,
①,
如图2,作于,
,,
,
又是中点,
②,
由(1)可知,,
,
③,
由①②③得:,即,
又,
.
(3)证明:如图,连接,
矩形中,是对角线的中点,
,
,
(等腰三角形的三线合一),
作于,则,,
,
,
,
,即,
又,
,
,
.
模拟考试 第3页(共6页) 模拟考试 第4页(共6页)
同课章节目录
