人教版(2019)必修第二册 6.4 生活中的圆周运动 课件(共21张PPT)
文档属性
| 名称 | 人教版(2019)必修第二册 6.4 生活中的圆周运动 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-22 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
生活中的圆周运动竖直平面内的圆周运动
汽车过拱桥
汽车过凹桥
绳的模型
———目 录———
01
02
03
04
杆的模型
复习提问:
1、处理匀速圆周运动问题的方法是什么?
合力=向心力
2、对于变速圆周运动又该如何处理呢?
把力沿着半径方向和切线方向分解;
沿半径方向的合力=向心力
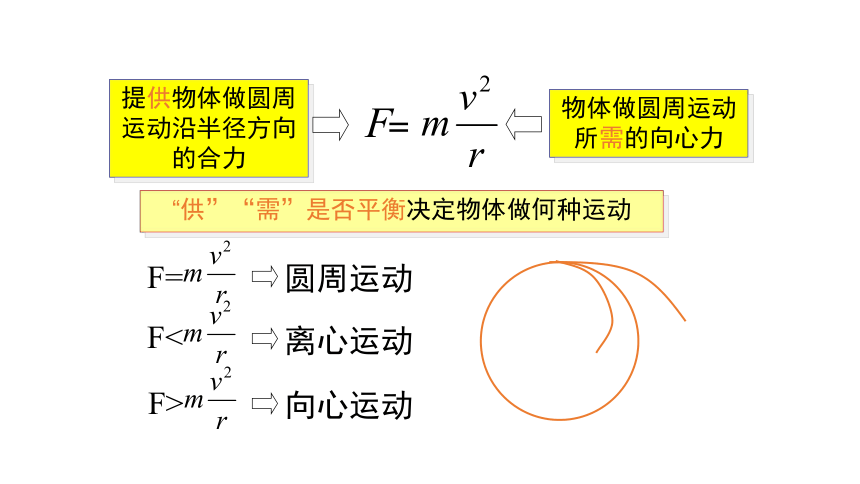
提供物体做圆周运动沿半径方向的合力
物体做圆周运动所需的向心力
“供”“需”是否平衡决定物体做何种运动
F
=
F=
圆周运动
F<
离心运动
向心运动
F>
PART
01
汽车过拱桥
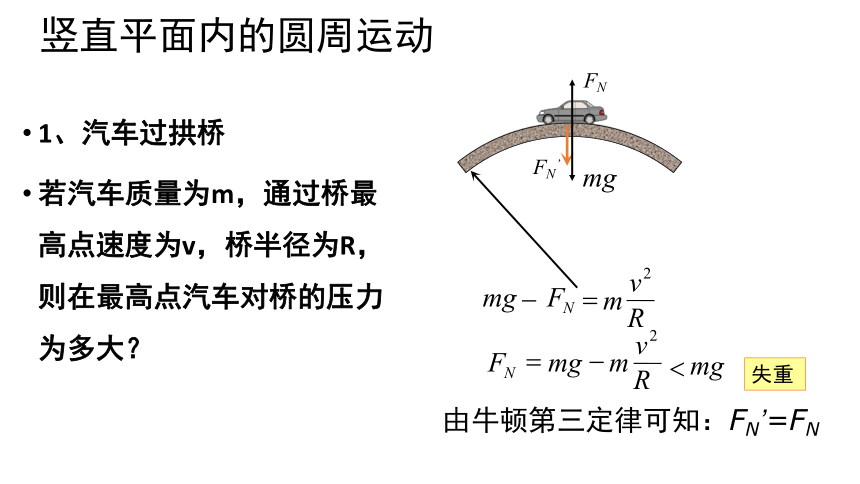
竖直平面内的圆周运动
1、汽车过拱桥
若汽车质量为m,通过桥最高点速度为v,桥半径为R,则在最高点汽车对桥的压力为多大?
FN
FN’
v
m
mg
F
N
-
=
2
R
v
m
mg
F
N
-
=
2
R
mg
mg
<
失重
由牛顿第三定律可知:FN’=FN
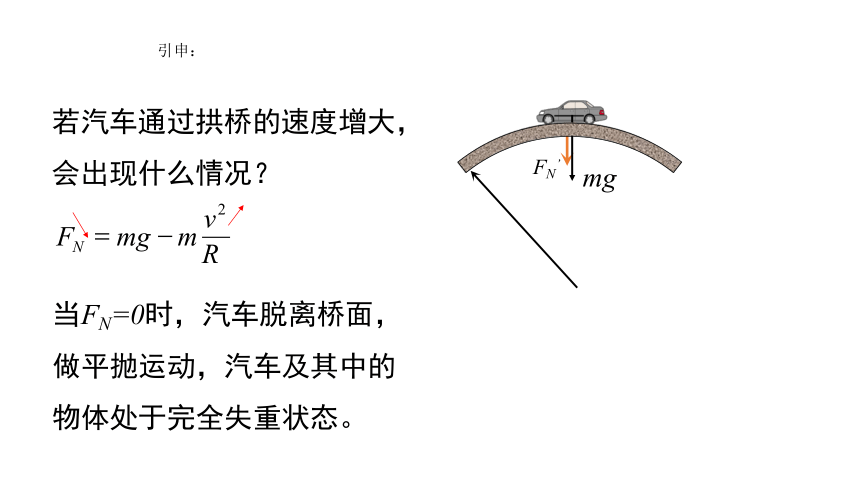
引申:
若汽车通过拱桥的速度增大,会出现什么情况?
v
m
mg
F
N
-
=
2
R
当FN=0时,汽车脱离桥面,做平抛运动,汽车及其中的物体处于完全失重状态。
FN’
mg
思考:
地球可以看做一个巨大的拱行桥,桥面的半径是地球半径(约为6400km)。地面上有一辆车,假设可以不断加速,会不会出现这样的情况:速度大到一定程度时,地面对车的支持力是0?
这时驾驶员与坐椅之间的压力是多少?驾驶员躯体各部分之间的压力是多少?他这时的可能有什么感觉?
PART
02
汽车过凹桥
竖直平面内的圆周运动
2、汽车过凹桥
FN
R
mg
>
mg
R
v
m
F
N
mg
=
2
-
R
v
m
mg
F
N
+
=
2
超重
有无可能做这样的运动?
若可能应满足怎样的条件?
mg
FN
r
思考:若汽车不在最高点或最低点,我们该怎样处理呢?
PART
03
绳的模型
绳的模型
PART
04
杆的模型
杆的模型
例 1
长为L的轻杆,一端固定一个小球,另一端固定在光滑的水平轴上,使小球在竖直平面内做圆周运动,关于小球在最高点的速度v,下列说法中正确的是( )
A.当v的值为时,杆对小球的弹力为零
B.当v由逐渐增大时,杆对小球的拉力逐渐增大
C.当v由逐渐减小时,杆对小球的支持力逐渐减小
D.当v由零逐渐增大时,向心力也逐渐增大
ABD
竖直平面内圆周运动的临界问题——“轻绳、 轻杆”模型
1.“轻绳”模型和“轻杆”模型不同的原因在于“轻绳”只能对小球产生拉力,而“轻杆”既可对小球产生拉力也可对小球产生支持力。
2.有关临界问题出现在变速圆周运动中,竖直平面内的圆周运动是典型的变速圆周运动,一般情况下,只讨论最高点和最低点的情况。
WHAT
01
汽车过拱桥
02
03
04
章节总结
汽车过凹桥
绳的模型
杆的模型
谢 谢 观 看
生活中的圆周运动竖直平面内的圆周运动
汽车过拱桥
汽车过凹桥
绳的模型
———目 录———
01
02
03
04
杆的模型
复习提问:
1、处理匀速圆周运动问题的方法是什么?
合力=向心力
2、对于变速圆周运动又该如何处理呢?
把力沿着半径方向和切线方向分解;
沿半径方向的合力=向心力
提供物体做圆周运动沿半径方向的合力
物体做圆周运动所需的向心力
“供”“需”是否平衡决定物体做何种运动
F
=
F=
圆周运动
F<
离心运动
向心运动
F>
PART
01
汽车过拱桥
竖直平面内的圆周运动
1、汽车过拱桥
若汽车质量为m,通过桥最高点速度为v,桥半径为R,则在最高点汽车对桥的压力为多大?
FN
FN’
v
m
mg
F
N
-
=
2
R
v
m
mg
F
N
-
=
2
R
mg
mg
<
失重
由牛顿第三定律可知:FN’=FN
引申:
若汽车通过拱桥的速度增大,会出现什么情况?
v
m
mg
F
N
-
=
2
R
当FN=0时,汽车脱离桥面,做平抛运动,汽车及其中的物体处于完全失重状态。
FN’
mg
思考:
地球可以看做一个巨大的拱行桥,桥面的半径是地球半径(约为6400km)。地面上有一辆车,假设可以不断加速,会不会出现这样的情况:速度大到一定程度时,地面对车的支持力是0?
这时驾驶员与坐椅之间的压力是多少?驾驶员躯体各部分之间的压力是多少?他这时的可能有什么感觉?
PART
02
汽车过凹桥
竖直平面内的圆周运动
2、汽车过凹桥
FN
R
mg
>
mg
R
v
m
F
N
mg
=
2
-
R
v
m
mg
F
N
+
=
2
超重
有无可能做这样的运动?
若可能应满足怎样的条件?
mg
FN
r
思考:若汽车不在最高点或最低点,我们该怎样处理呢?
PART
03
绳的模型
绳的模型
PART
04
杆的模型
杆的模型
例 1
长为L的轻杆,一端固定一个小球,另一端固定在光滑的水平轴上,使小球在竖直平面内做圆周运动,关于小球在最高点的速度v,下列说法中正确的是( )
A.当v的值为时,杆对小球的弹力为零
B.当v由逐渐增大时,杆对小球的拉力逐渐增大
C.当v由逐渐减小时,杆对小球的支持力逐渐减小
D.当v由零逐渐增大时,向心力也逐渐增大
ABD
竖直平面内圆周运动的临界问题——“轻绳、 轻杆”模型
1.“轻绳”模型和“轻杆”模型不同的原因在于“轻绳”只能对小球产生拉力,而“轻杆”既可对小球产生拉力也可对小球产生支持力。
2.有关临界问题出现在变速圆周运动中,竖直平面内的圆周运动是典型的变速圆周运动,一般情况下,只讨论最高点和最低点的情况。
WHAT
01
汽车过拱桥
02
03
04
章节总结
汽车过凹桥
绳的模型
杆的模型
谢 谢 观 看
