2.2.1对数与对数运算--对数的概念 课件
文档属性
| 名称 | 2.2.1对数与对数运算--对数的概念 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-08 16:49:56 | ||
图片预览





文档简介
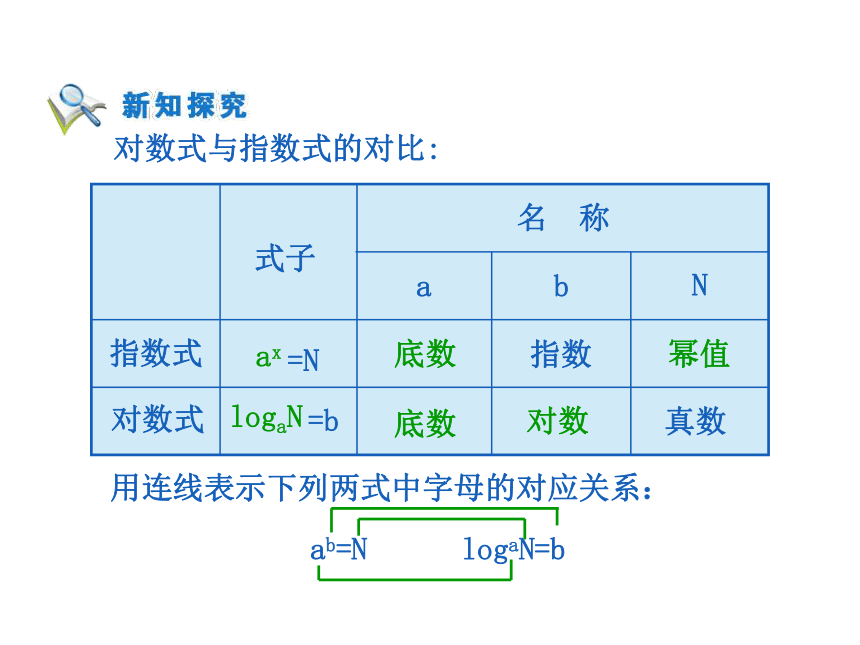
课件17张PPT。对数的概念你能用等式表示数字9,3,2之间的关系吗? 一般地,如果ax=N(a>0,且a≠1),那么数
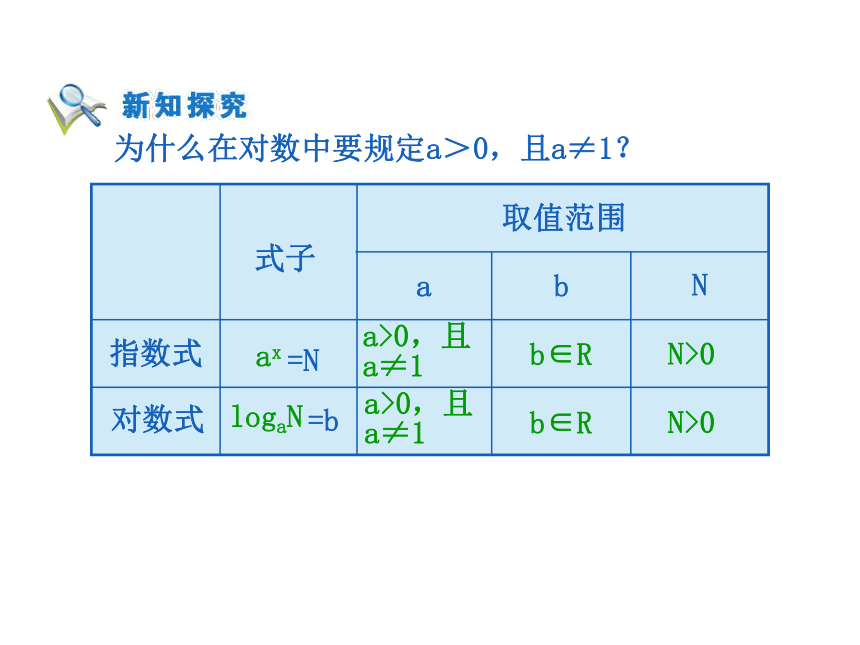
x叫做以a为底N的对数(logarithm),记作: 其中a叫做对数的底数,N叫做真数。 logaN 对数式与指数式的对比:ax 底数 对数 幂值 底数 b∈R logaN 为什么在对数中要规定a>0,且a≠1?ax a>0,且
a≠1 N>0 a>0,且
a≠1 b∈R N>0 通常我们将以10为底的对数叫做常用对数
(common logarithm),并把log10N记为: 在科学技术中常使用以无理数e=2.71828…
为底数的对数,以e为底的对数称为自然对数
(natural logarithm),并且把logeN记为: 讨论:你能用对数表示2x=-3和2x=0吗?为什么? (1) 负数和零没有对数; 在中,必须logaN>0,这是由于在实数范围
内,正数的任何次幂都是正数,因而ax=N中N总
是正数。(2) 对任意的a>0且a≠1,都有a0=1。
所以loga1=0(3) 对任意的a>0且a≠1,都有a1=a。
所以logaa=1 将下列指数式化为对数式 将下列对数式化为指数式求下列各式中的x值= 4-2又x>0求下列各式中的x值解:(3)因为lg100 = x,所以10x = 100 10x = 102, 于是x = 2 (4)因为-lne2 = x, 所以lne2 = -x,e2 = e-x, 于是x = -2 将下列指数式写成对数式解:(1)3 = log28 (3)x = log1025将下列对数式写成指数式解:(1)5x = 27(3)10x = 0.3将下列指数式写成对数式解:(1)设x = log225, 则5x = 25 = 52所以x = 2 = 2-4所以x = -4 将下列指数式写成对数式解:则10x = 0.001 = 10-3所以x = -3 (5)设x = log1515, 则x = 1 (6)设x = log0.41, 则x = 0(4)设x = lg0.001, 若ax=N(a>0,且a≠1),那么数x叫做以a为
底N的对数(logarithm),记当x=logaN,当a=10
时称作常用对数,而a=e时,则称自然对数。 16世纪末至17世纪初的时候,当时在自然
科学领域(特别是天文学)的发展上经常遇到大
量精密而又庞大的数值计算,于是数学家们为
了寻求化简的计算方法而发明了对数。 1624年,英国的布里格斯创造了常用对数。
1619年,伦敦斯彼得所著的《新对数》使对
对数与自然对数更接近(以e=2.71828...为
底)。
对数的发明为当时社会的发展起了重要的影
响:伽利略说:给我时间,空间和对数,我
可以创造出一个宇宙。
数学家拉普拉斯说:对数用缩短计算的时间
来使天文学家的寿命加倍 。
x叫做以a为底N的对数(logarithm),记作: 其中a叫做对数的底数,N叫做真数。 logaN 对数式与指数式的对比:ax 底数 对数 幂值 底数 b∈R logaN 为什么在对数中要规定a>0,且a≠1?ax a>0,且
a≠1 N>0 a>0,且
a≠1 b∈R N>0 通常我们将以10为底的对数叫做常用对数
(common logarithm),并把log10N记为: 在科学技术中常使用以无理数e=2.71828…
为底数的对数,以e为底的对数称为自然对数
(natural logarithm),并且把logeN记为: 讨论:你能用对数表示2x=-3和2x=0吗?为什么? (1) 负数和零没有对数; 在中,必须logaN>0,这是由于在实数范围
内,正数的任何次幂都是正数,因而ax=N中N总
是正数。(2) 对任意的a>0且a≠1,都有a0=1。
所以loga1=0(3) 对任意的a>0且a≠1,都有a1=a。
所以logaa=1 将下列指数式化为对数式 将下列对数式化为指数式求下列各式中的x值= 4-2又x>0求下列各式中的x值解:(3)因为lg100 = x,所以10x = 100 10x = 102, 于是x = 2 (4)因为-lne2 = x, 所以lne2 = -x,e2 = e-x, 于是x = -2 将下列指数式写成对数式解:(1)3 = log28 (3)x = log1025将下列对数式写成指数式解:(1)5x = 27(3)10x = 0.3将下列指数式写成对数式解:(1)设x = log225, 则5x = 25 = 52所以x = 2 = 2-4所以x = -4 将下列指数式写成对数式解:则10x = 0.001 = 10-3所以x = -3 (5)设x = log1515, 则x = 1 (6)设x = log0.41, 则x = 0(4)设x = lg0.001, 若ax=N(a>0,且a≠1),那么数x叫做以a为
底N的对数(logarithm),记当x=logaN,当a=10
时称作常用对数,而a=e时,则称自然对数。 16世纪末至17世纪初的时候,当时在自然
科学领域(特别是天文学)的发展上经常遇到大
量精密而又庞大的数值计算,于是数学家们为
了寻求化简的计算方法而发明了对数。 1624年,英国的布里格斯创造了常用对数。
1619年,伦敦斯彼得所著的《新对数》使对
对数与自然对数更接近(以e=2.71828...为
底)。
对数的发明为当时社会的发展起了重要的影
响:伽利略说:给我时间,空间和对数,我
可以创造出一个宇宙。
数学家拉普拉斯说:对数用缩短计算的时间
来使天文学家的寿命加倍 。
