对数函数的图象及其性质
图片预览



文档简介
课件26张PPT。对数函数的图象及其性质 选取底数(a>0且a≠1)的若干个不同的值,
在同一平面直角坐标系内作出相应的对数函数的
图象。观察图象,你能发现它们有哪些共同特征
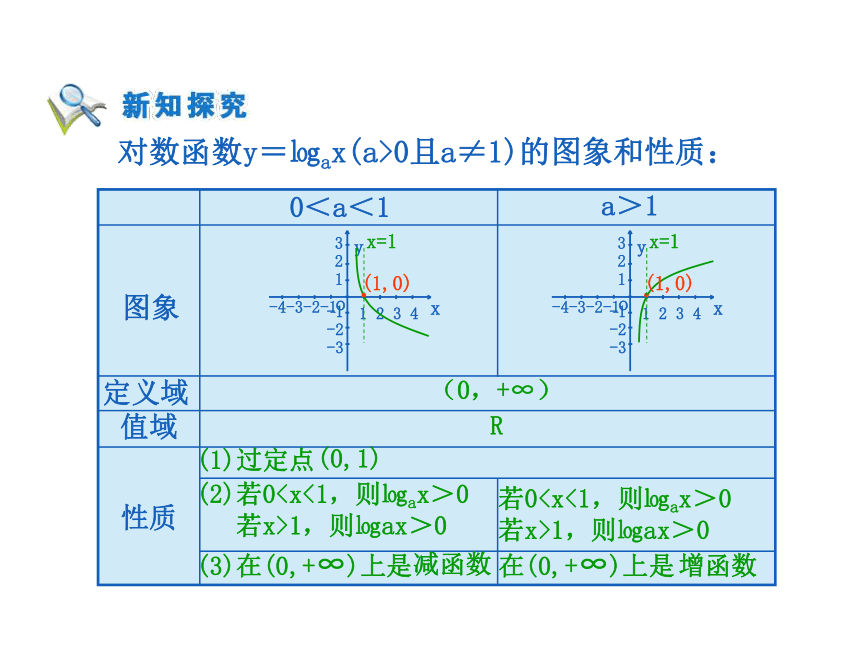
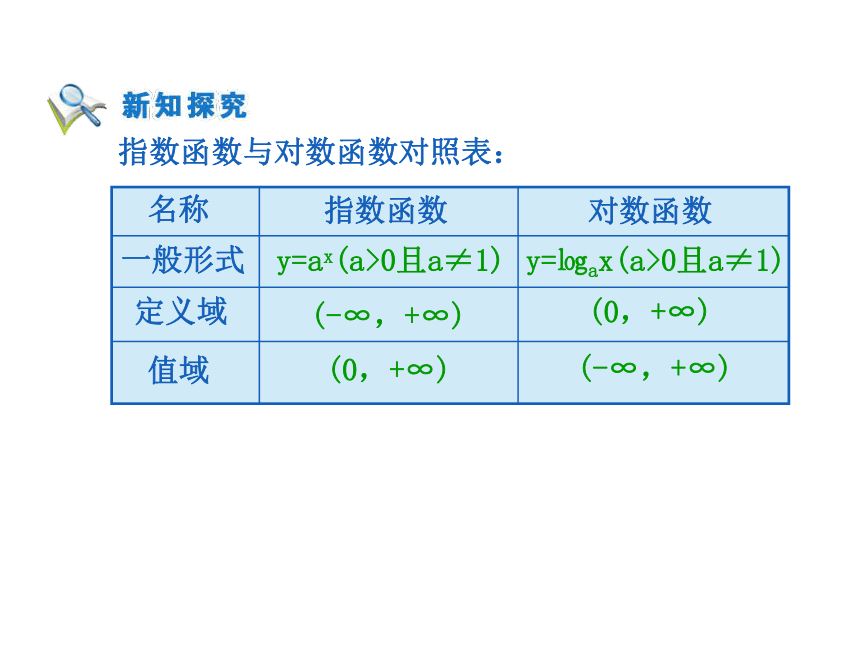
吗?对数函数的图象对数函数y=㏒ax(a>0且a≠1)的图象和性质:(1)过定点 (0,+∞) R (0,1) (2)若0 若x>1,则㏒ax>0若0若x>1,则㏒ax>0指数函数与对数函数对照表:y=ax(a>0且a≠1) y=㏒ax(a>0且a≠1) (-∞,+∞) (0,+∞) (0,+∞) (-∞,+∞) 指数函数与对数函数对照表:当a>1时:
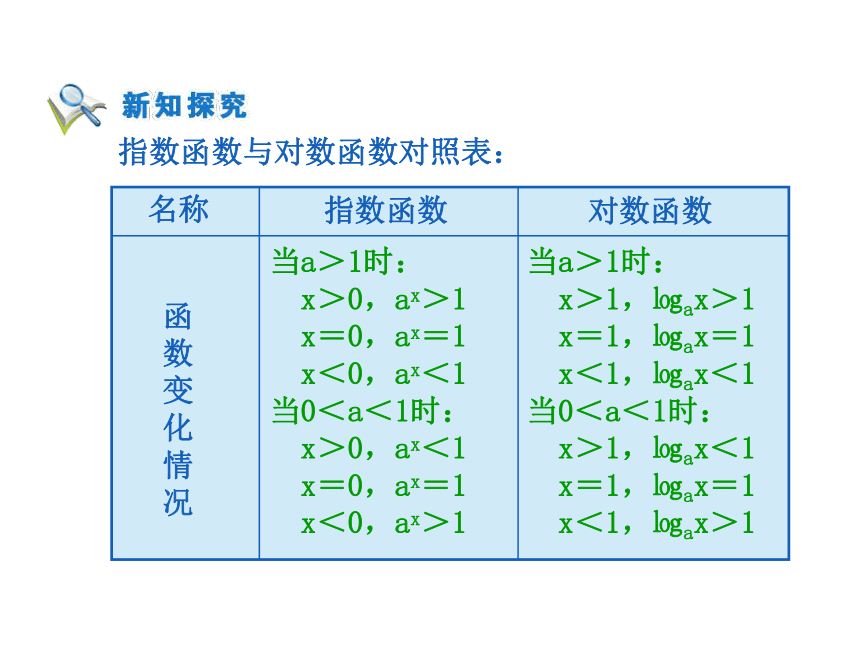
x>0,ax>1
x=0,ax=1
x<0,ax<1
当0<a<1时:
x>0,ax<1
x=0,ax=1
x<0,ax>1当a>1时:
x>1,㏒ax>1
x=1,㏒ax=1
x<1,㏒ax<1
当0<a<1时:
x>1,㏒ax<1
x=1,㏒ax=1
x<1,㏒ax>1指数函数与对数函数对照表:当a>1时,
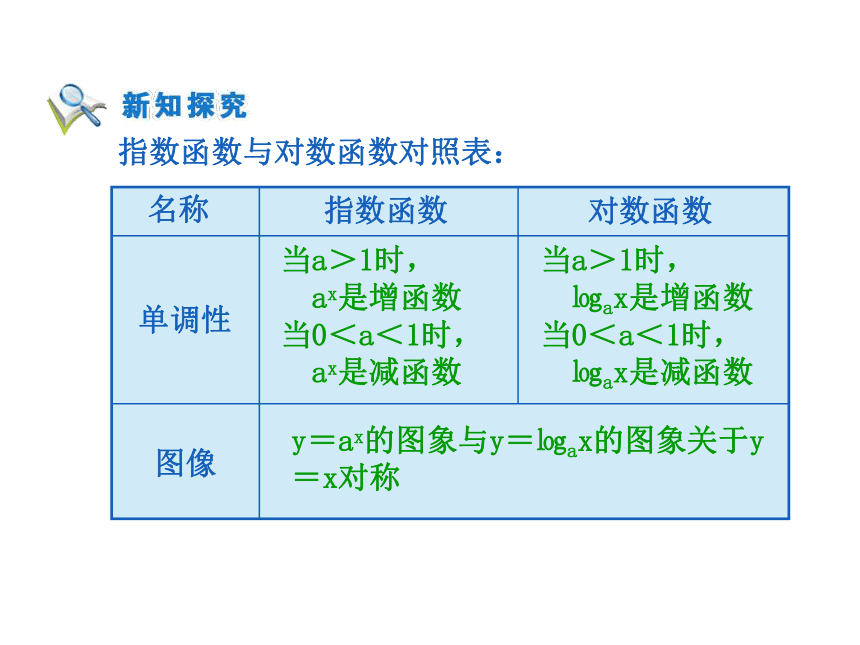
ax是增函数
当0<a<1时,
ax是减函数当a>1时,
㏒ax是增函数
当0<a<1时,
㏒ax是减函数y=ax的图象与y=㏒ax的图象关于y=x对称 (1)㏒23.4,㏒28.5 (2)㏒0.31.8,㏒0.32.7
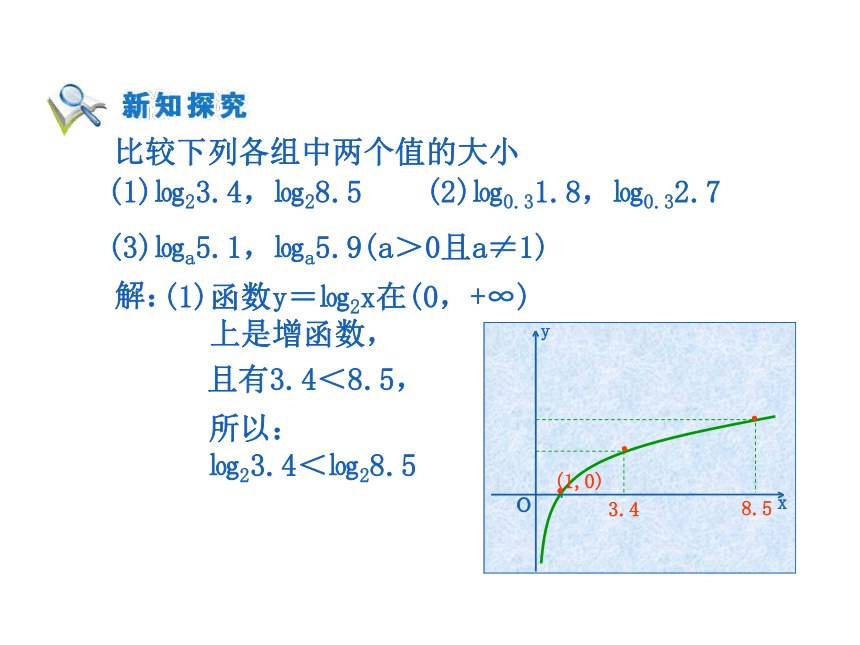
(3)㏒a5.1,㏒a5.9(a>0且a≠1)比较下列各组中两个值的大小解: (1)函数y=㏒2x在(0,+∞)
上是增函数, 且有3.4<8.5, 所以:
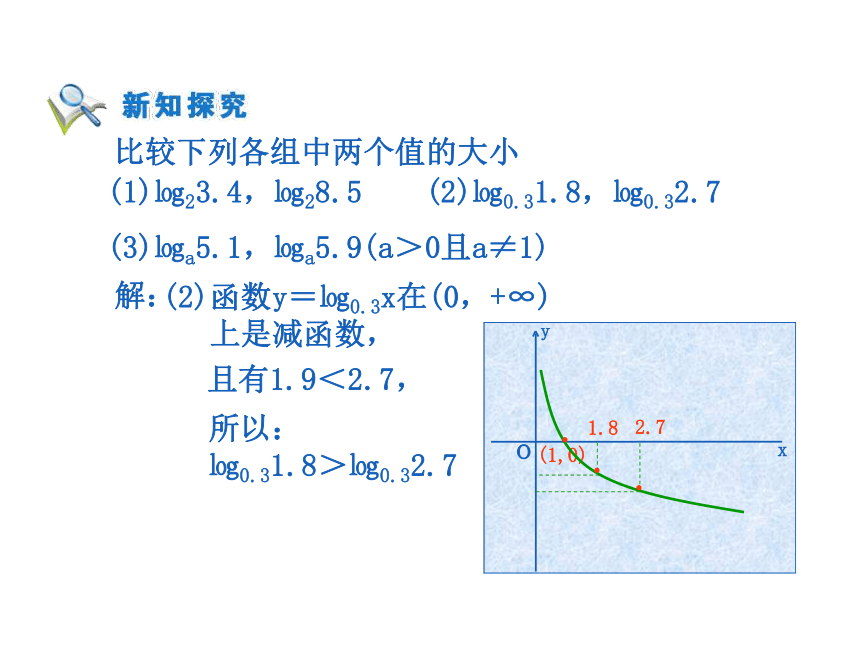
㏒23.4<㏒28.5 比较下列各组中两个值的大小解: (2)函数y=㏒0.3x在(0,+∞)
上是减函数, 且有1.9<2.7, 所以:
㏒0.31.8>㏒0.32.7 (1)㏒23.4,㏒28.5 (2)㏒0.31.8,㏒0.32.7
(3)㏒a5.1,㏒a5.9(a>0且a≠1)比较下列各组中两个值的大小解: 当a>1时,函数y=㏒ax
在(0,+∞)上是增函数, 且有5.1<5.9, 所以:
㏒a5.1<㏒a5.9 (3)对数函数的增减性取决于对数的底数a
是大于1还是小于1,因此在这个题目中
要对底数a进行讨论。 (1)㏒23.4,㏒28.5 (2)㏒0.31.8,㏒0.32.7
(3)㏒a5.1,㏒a5.9(a>0且a≠1)比较下列各组中两个值的大小解: 当0 在(0,+∞)上是减函数, 且有5.1<5.9, 所以:
㏒a5.1>㏒a5.9 (3)对数函数的增减性取决于对数的底数a
是大于1还是小于1,因此在这个题目中
要对底数a进行讨论。 (1)㏒23.4,㏒28.5 (2)㏒0.31.8,㏒0.32.7
(3)㏒a5.1,㏒a5.9(a>0且a≠1)在(0,+∞)上,随着[H+]的增大, 即PH减小。 (1)根据对数函数性质及上述PH的计算公式,
说明溶液酸碱度与溶液中氢离子的浓度之间的
变化关系;(1)根据对数函数性质及上述PH的计算公式,
说明溶液酸碱度与溶液中氢离子的浓度之间的
变化关系;解:所以,随着[H+]的增大,PH减小,即溶液
中氢离子的浓度越大,溶液的酸碱度就越
大。 溶液酸碱度是通过PH刻画的。PH的计算公
式为PH=- [H+],其中[H+]表示溶液中氢离子
的浓度,单位是摩尔/升。 溶液酸碱度是通过PH刻画的。PH的计算公
式为PH=- [H+],其中[H+]表示溶液中氢离子
的浓度,单位是摩尔/升。(2)已知纯净水中氢离子的浓度为[H+]=10-7摩
尔/升,计算纯净水的PH。解:(2)当[H+]=10-7时, =-7 所以纯净水的PH是7。 事实上,食品监督检测部门检测纯净水的
质量时,需要检测很多项目。PH的检测只是其
中的一项。国家标准规定,饮用纯净水的PH应
该在5.0~7.0之间,你知道为什么吗? 探究:过y轴正半轴上任意一点作x轴的平行线,与y=2x
的图象 交点
对任意一个y∈(0,+∞),通过x=㏒2y式子,x在
R中都有 的值和它对应。
函数x=㏒2y(y∈(0,+∞))是函数y=2x(x∈R)的
。有且只有一个 唯一确定 反函数 我们习惯上把x表示自变量,y表示函数,因
此对调函数x=㏒2y中的字母x,y,写成y=㏒2x。 函数y=㏒2x(x∈(0,+∞))是函数y=2x
(x∈R)的反函数。 同底的对数函数和指数函数互为反函数。 对数函数y=㏒2x(a>0且a≠1)和指数函数
y=2x(a>0且a≠1)互为反函数 (1)㏒53,㏒54 (2)㏒0.12,㏒0.19
(3)㏒1.61.7,㏒1.61.5 利用函数图象或函数的单调性比较下列各题中两个值的大小解: (1)㏒53<㏒54 (2)㏒0.12>㏒0.19 (3)㏒1.61.7>㏒1.61.5 (1)㏒5m<㏒5n (2)㏒0.5m>㏒0.5n
(3)㏒am>㏒an(a>0且a≠1)已知下列不等式,比较正数m,n的大小解: (1)因为y=㏒5x在(0,+∞)上是 且有㏒5m<㏒5n,(2)因为y=㏒0.5x在(0,+∞)上是 ㏒0.5m<㏒0.5n,所以m<n 所以m>n 增函数 减函数 (1)㏒5m<㏒5n (2)㏒0.5m>㏒0.5n
(3)㏒am>㏒an(a>0且a≠1)已知下列不等式,比较正数m,n的大小解: (3)当a>1时, 且有㏒am>㏒an, 当0<a<1时, ㏒0.5m>㏒0.5n,所以m>n 所以m<n 增函数, 减函数, y=㏒5x在(0,+∞)上是 y=㏒0.5x在(0,+∞) 上是时(1)试说明哪个函数对应于哪个图象,并解释为
什么?(2)以已有图象为基础,在同一坐标系中画出 y=㏒3x y=㏒5x (1)当一条鱼的耗氧量是2700个单位时,它的游
速是多少?解:令O=2700, 得出v=1.5 所以鲑鱼的游速为1.5米/秒。 (2)计算一条鱼静止时耗氧量的单位数。 解:鱼静止时速度v=0, 得出O=100 所以一条鱼静止时的耗氧量为100个单位。 巧用数学看现实 某报纸上报道了两则广告,甲商厦实行有
奖销售:特等奖10000元 1名,一等奖1000元
2名,二等奖100元10名,三等奖5元200名,乙
商厦则实行九五折优惠销售。请你想一想;假
如你是消费者,你更愿意去哪一家商厦?哪一
家商厦提供给销费者的实惠大? 巧用数学看现实 一、苦甲商厦确定每组设奖,当参加人数
较少时,少于213(1十2+10+200=213人)人,
人们会认为获奖机率较大,则甲商厦的销售方
式更吸引顾客。 二、若甲商厦的每组营业额较多时,它给
顾客的优惠幅度就相应的小。因为甲商厦提供
的优惠金额是固定的,共14000元(10000+
2000+1000+1000=14000)。假设两商厦提
供的优惠都是14000元,则可求乙商厦的营业
额为280000元(14000÷5%=280000)。
在同一平面直角坐标系内作出相应的对数函数的
图象。观察图象,你能发现它们有哪些共同特征
吗?对数函数的图象对数函数y=㏒ax(a>0且a≠1)的图象和性质:(1)过定点 (0,+∞) R (0,1) (2)若0
x>0,ax>1
x=0,ax=1
x<0,ax<1
当0<a<1时:
x>0,ax<1
x=0,ax=1
x<0,ax>1当a>1时:
x>1,㏒ax>1
x=1,㏒ax=1
x<1,㏒ax<1
当0<a<1时:
x>1,㏒ax<1
x=1,㏒ax=1
x<1,㏒ax>1指数函数与对数函数对照表:当a>1时,
ax是增函数
当0<a<1时,
ax是减函数当a>1时,
㏒ax是增函数
当0<a<1时,
㏒ax是减函数y=ax的图象与y=㏒ax的图象关于y=x对称 (1)㏒23.4,㏒28.5 (2)㏒0.31.8,㏒0.32.7
(3)㏒a5.1,㏒a5.9(a>0且a≠1)比较下列各组中两个值的大小解: (1)函数y=㏒2x在(0,+∞)
上是增函数, 且有3.4<8.5, 所以:
㏒23.4<㏒28.5 比较下列各组中两个值的大小解: (2)函数y=㏒0.3x在(0,+∞)
上是减函数, 且有1.9<2.7, 所以:
㏒0.31.8>㏒0.32.7 (1)㏒23.4,㏒28.5 (2)㏒0.31.8,㏒0.32.7
(3)㏒a5.1,㏒a5.9(a>0且a≠1)比较下列各组中两个值的大小解: 当a>1时,函数y=㏒ax
在(0,+∞)上是增函数, 且有5.1<5.9, 所以:
㏒a5.1<㏒a5.9 (3)对数函数的增减性取决于对数的底数a
是大于1还是小于1,因此在这个题目中
要对底数a进行讨论。 (1)㏒23.4,㏒28.5 (2)㏒0.31.8,㏒0.32.7
(3)㏒a5.1,㏒a5.9(a>0且a≠1)比较下列各组中两个值的大小解: 当0
㏒a5.1>㏒a5.9 (3)对数函数的增减性取决于对数的底数a
是大于1还是小于1,因此在这个题目中
要对底数a进行讨论。 (1)㏒23.4,㏒28.5 (2)㏒0.31.8,㏒0.32.7
(3)㏒a5.1,㏒a5.9(a>0且a≠1)在(0,+∞)上,随着[H+]的增大, 即PH减小。 (1)根据对数函数性质及上述PH的计算公式,
说明溶液酸碱度与溶液中氢离子的浓度之间的
变化关系;(1)根据对数函数性质及上述PH的计算公式,
说明溶液酸碱度与溶液中氢离子的浓度之间的
变化关系;解:所以,随着[H+]的增大,PH减小,即溶液
中氢离子的浓度越大,溶液的酸碱度就越
大。 溶液酸碱度是通过PH刻画的。PH的计算公
式为PH=- [H+],其中[H+]表示溶液中氢离子
的浓度,单位是摩尔/升。 溶液酸碱度是通过PH刻画的。PH的计算公
式为PH=- [H+],其中[H+]表示溶液中氢离子
的浓度,单位是摩尔/升。(2)已知纯净水中氢离子的浓度为[H+]=10-7摩
尔/升,计算纯净水的PH。解:(2)当[H+]=10-7时, =-7 所以纯净水的PH是7。 事实上,食品监督检测部门检测纯净水的
质量时,需要检测很多项目。PH的检测只是其
中的一项。国家标准规定,饮用纯净水的PH应
该在5.0~7.0之间,你知道为什么吗? 探究:过y轴正半轴上任意一点作x轴的平行线,与y=2x
的图象 交点
对任意一个y∈(0,+∞),通过x=㏒2y式子,x在
R中都有 的值和它对应。
函数x=㏒2y(y∈(0,+∞))是函数y=2x(x∈R)的
。有且只有一个 唯一确定 反函数 我们习惯上把x表示自变量,y表示函数,因
此对调函数x=㏒2y中的字母x,y,写成y=㏒2x。 函数y=㏒2x(x∈(0,+∞))是函数y=2x
(x∈R)的反函数。 同底的对数函数和指数函数互为反函数。 对数函数y=㏒2x(a>0且a≠1)和指数函数
y=2x(a>0且a≠1)互为反函数 (1)㏒53,㏒54 (2)㏒0.12,㏒0.19
(3)㏒1.61.7,㏒1.61.5 利用函数图象或函数的单调性比较下列各题中两个值的大小解: (1)㏒53<㏒54 (2)㏒0.12>㏒0.19 (3)㏒1.61.7>㏒1.61.5 (1)㏒5m<㏒5n (2)㏒0.5m>㏒0.5n
(3)㏒am>㏒an(a>0且a≠1)已知下列不等式,比较正数m,n的大小解: (1)因为y=㏒5x在(0,+∞)上是 且有㏒5m<㏒5n,(2)因为y=㏒0.5x在(0,+∞)上是 ㏒0.5m<㏒0.5n,所以m<n 所以m>n 增函数 减函数 (1)㏒5m<㏒5n (2)㏒0.5m>㏒0.5n
(3)㏒am>㏒an(a>0且a≠1)已知下列不等式,比较正数m,n的大小解: (3)当a>1时, 且有㏒am>㏒an, 当0<a<1时, ㏒0.5m>㏒0.5n,所以m>n 所以m<n 增函数, 减函数, y=㏒5x在(0,+∞)上是 y=㏒0.5x在(0,+∞) 上是时(1)试说明哪个函数对应于哪个图象,并解释为
什么?(2)以已有图象为基础,在同一坐标系中画出 y=㏒3x y=㏒5x (1)当一条鱼的耗氧量是2700个单位时,它的游
速是多少?解:令O=2700, 得出v=1.5 所以鲑鱼的游速为1.5米/秒。 (2)计算一条鱼静止时耗氧量的单位数。 解:鱼静止时速度v=0, 得出O=100 所以一条鱼静止时的耗氧量为100个单位。 巧用数学看现实 某报纸上报道了两则广告,甲商厦实行有
奖销售:特等奖10000元 1名,一等奖1000元
2名,二等奖100元10名,三等奖5元200名,乙
商厦则实行九五折优惠销售。请你想一想;假
如你是消费者,你更愿意去哪一家商厦?哪一
家商厦提供给销费者的实惠大? 巧用数学看现实 一、苦甲商厦确定每组设奖,当参加人数
较少时,少于213(1十2+10+200=213人)人,
人们会认为获奖机率较大,则甲商厦的销售方
式更吸引顾客。 二、若甲商厦的每组营业额较多时,它给
顾客的优惠幅度就相应的小。因为甲商厦提供
的优惠金额是固定的,共14000元(10000+
2000+1000+1000=14000)。假设两商厦提
供的优惠都是14000元,则可求乙商厦的营业
额为280000元(14000÷5%=280000)。
