几类不同增长的函数模型第一课时
文档属性
| 名称 | 几类不同增长的函数模型第一课时 |

|
|
| 格式 | zip | ||
| 文件大小 | 156.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-09 00:00:00 | ||
图片预览




文档简介
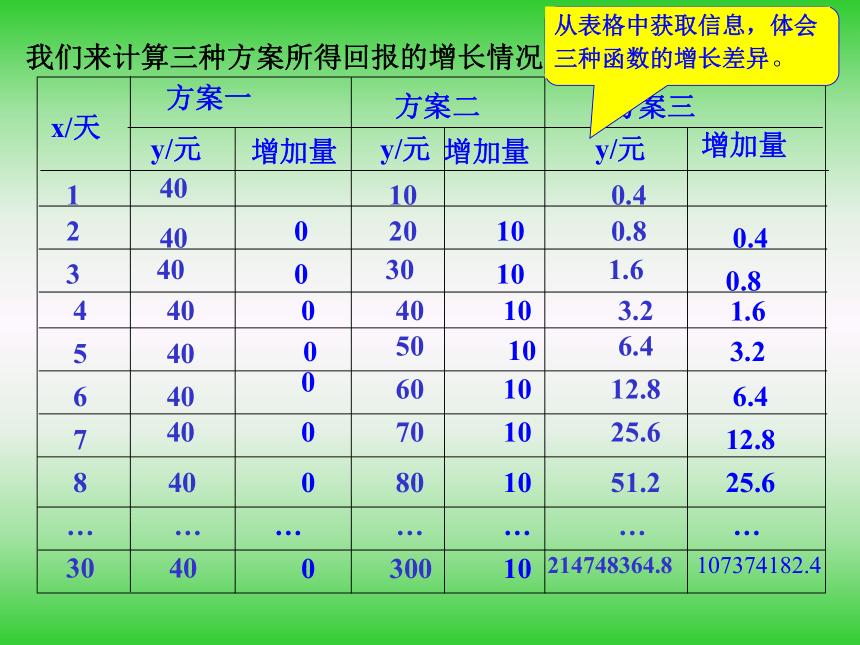
课件14张PPT。几类不同增长的函数模型澳大利亚兔子数“爆炸” 有一大群喝水、嬉戏的兔子,但是这群兔子曾使澳大利亚伤透了脑筋.1859年,有人从欧洲带进澳洲几只兔子,由于澳洲有茂盛的牧草,而且没有兔子的天敌,兔子数量不断增加,不到100年,兔子们占领了整个澳大利亚,数量达到75亿只.可爱的兔子变得可恶起来,75亿只兔子吃掉了相当于75亿只羊所吃的牧草,草原的载畜率大大降低,而牛羊是澳大利亚的主要牲口.这使澳大利亚头痛不已,他们采用各种方法消灭这些兔子,直至二十世纪五十年代,科学家采用载液瘤病毒杀死了百分之九十的野兔,澳大利亚人才算松了一口气.我们来看两个具体问题: 例1 假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元
方案二:第一天回报10元,以后每天比前一天多回报10元
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
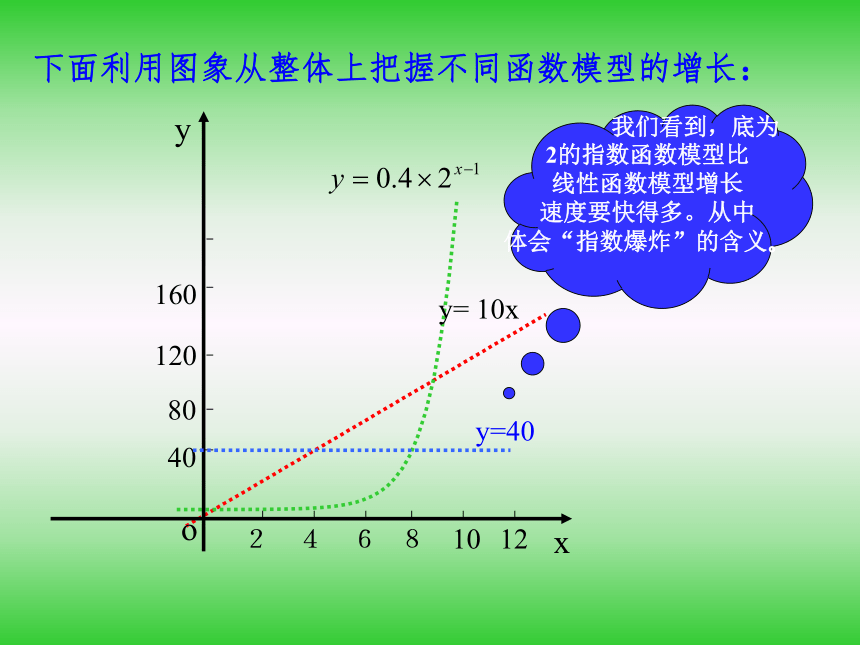
请问,你会选择哪种投资方案? 问题:在例1中,涉及哪些数量关系?如何用函数描述这些数量关系?分析:先建立三种方案所对应的函数模型:y=40,y=10x, 。通过比较它们的增长情况,为选择投资方案提供依据。我们来计算三种方案所得回报的增长情况:1234040400010203010100.40.81.60.40.8下面利用图象从整体上把握不同函数模型的增长: 我们看到,底为
2的指数函数模型比
线性函数模型增长
速度要快得多。从中
体会“指数爆炸”的含义。
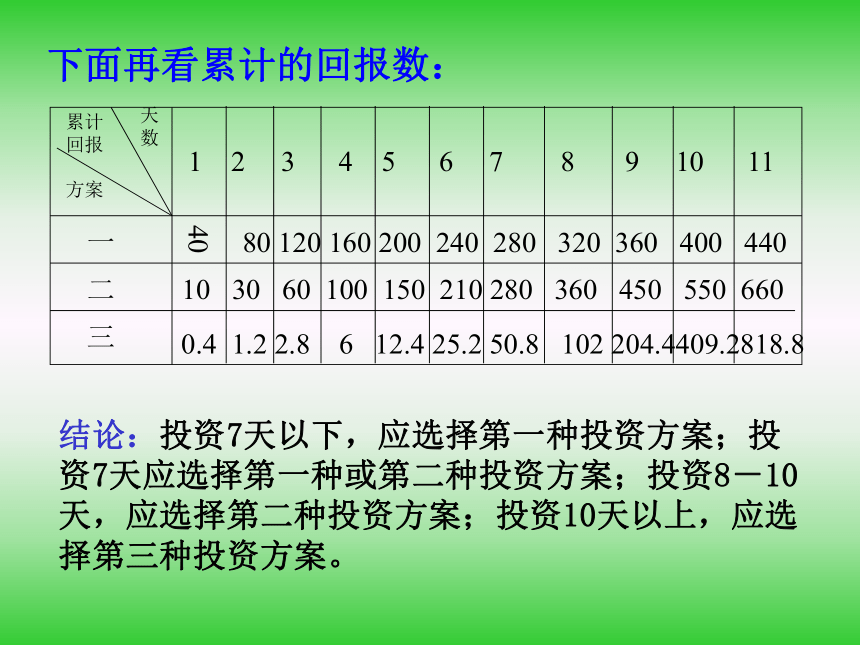
yxoy=40y= 10x下面再看累计的回报数:结论:投资7天以下,应选择第一种投资方案;投资7天应选择第一种或第二种投资方案;投资8-10天,应选择第二种投资方案;投资10天以上,应选择第三种投资方案。一二三401 2 3 4 5 6 7 8 9 10 1180 120 160 200 240 280 320 360 400 440 10 30 60 100 150 210 280 360 450 550 6600.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4409.2818.8例2 某公司为了实现1000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:
y=0.25X, , ,其中哪个模型能符合公司的要求?
问题:例2涉及了哪几类函数模型?本例的实质是什么?我们不妨先作出函数图象:通过观察函数图象得到初步结论:按对数模型进行奖励时符合公司的要求。xyoy=5y=0.25x下面列表计算确认上述判断:xyo我们来看函数 的图象:问题:当 时,奖金是否不超过利润的25%呢?从以上两个例子,我们看到对数函数,指数函数和幂函数在第一区间的增长是有差异的,下面用几何画板来观察它们的差异.小结
确定函数模型利用数据表格、函数体会直线上升、指数作业:
1.课本107页A1,2,B1
2.举出生活实例,并用函数模型进行分析。图象讨论模型爆炸、对数增长等不同类型函数的含义。
方案一:每天回报40元
方案二:第一天回报10元,以后每天比前一天多回报10元
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案? 问题:在例1中,涉及哪些数量关系?如何用函数描述这些数量关系?分析:先建立三种方案所对应的函数模型:y=40,y=10x, 。通过比较它们的增长情况,为选择投资方案提供依据。我们来计算三种方案所得回报的增长情况:1234040400010203010100.40.81.60.40.8下面利用图象从整体上把握不同函数模型的增长: 我们看到,底为
2的指数函数模型比
线性函数模型增长
速度要快得多。从中
体会“指数爆炸”的含义。
yxoy=40y= 10x下面再看累计的回报数:结论:投资7天以下,应选择第一种投资方案;投资7天应选择第一种或第二种投资方案;投资8-10天,应选择第二种投资方案;投资10天以上,应选择第三种投资方案。一二三401 2 3 4 5 6 7 8 9 10 1180 120 160 200 240 280 320 360 400 440 10 30 60 100 150 210 280 360 450 550 6600.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4409.2818.8例2 某公司为了实现1000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:
y=0.25X, , ,其中哪个模型能符合公司的要求?
问题:例2涉及了哪几类函数模型?本例的实质是什么?我们不妨先作出函数图象:通过观察函数图象得到初步结论:按对数模型进行奖励时符合公司的要求。xyoy=5y=0.25x下面列表计算确认上述判断:xyo我们来看函数 的图象:问题:当 时,奖金是否不超过利润的25%呢?从以上两个例子,我们看到对数函数,指数函数和幂函数在第一区间的增长是有差异的,下面用几何画板来观察它们的差异.小结
确定函数模型利用数据表格、函数体会直线上升、指数作业:
1.课本107页A1,2,B1
2.举出生活实例,并用函数模型进行分析。图象讨论模型爆炸、对数增长等不同类型函数的含义。
