1.1.3 集合的基本运算(并集与交集)
文档属性
| 名称 | 1.1.3 集合的基本运算(并集与交集) |

|
|
| 格式 | zip | ||
| 文件大小 | 357.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-10 00:00:00 | ||
图片预览





文档简介
课件12张PPT。第一章 1.1.3集合间的基本运算(并集与交集)教学目标:
1.正确理解并集与交集的概念。
2.会求两个已知集合的并集与交集。
3.通过韦恩图、数轴的利用,提高运用数形结合解决问题的能力。
教学重点:
并集、交集的概念,数形结合思想。
教学难点:
理解并集与交集的概念、符号之间的区别与联系.
教学方法:
发现式教学法必修①总第 4 课时复习引入1.子集、真子集的概念是怎样的? 2.子集、真子集有哪些性质? 集合间的基本运算(一)3.两个实数可以进行加、减、乘、除四则运算,那么两个集合是否也可以进行某种运算呢? 一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,记作 A∪B ,即A∪B={x | x∈A,或x∈B} 读作 A并 B 定义:并集观察集合A,B,C元素间的关系: A={4,5,6,8}, B={3,5,7,8},
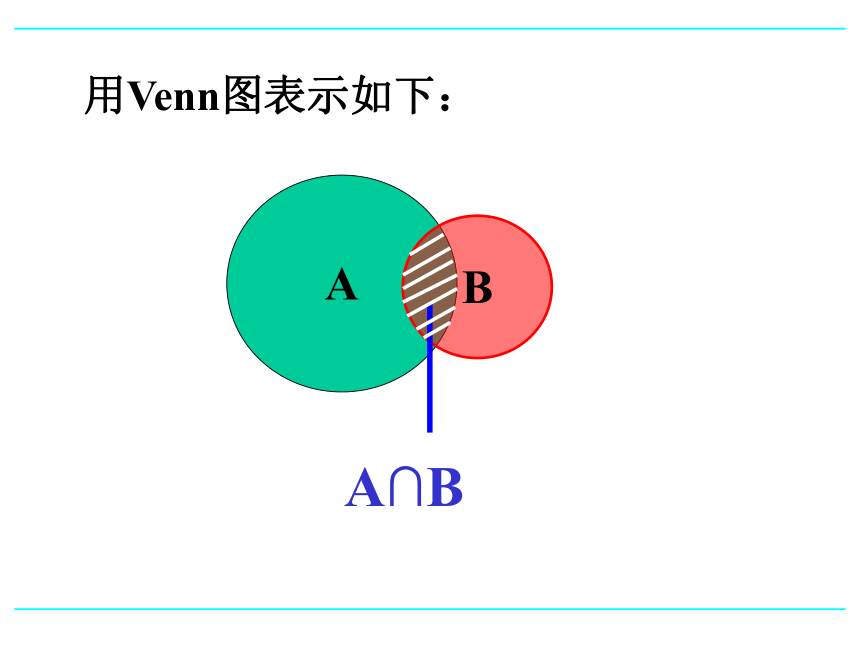
C={3,4,5,6,7,8} 思考ABA∪B用Venn图表示如下: 一般地,由属于集合A且属于集合B的所有元素组成的集合叫做A与B的交集,即A∩B={x | x∈A,且x∈B} 读作 A交 B 定义:交集观察集合A,B,C元素间的关系: A={4,5,6,8}, B={3,5,7,8},
C={5,8} 思考记作 A∩B,ABA∩B用Venn图表示如下:(1) A∩A = A∩φ = (2) A∪A = A∪φ =AAφA==A∪B B∪AA∩B B∩A(3) A∩B A A∩B B(4) A A∪B B A∪B 性质⑸ 若A∩B=A,则A B.反之,亦然.⑹ 若A∪B=A,则A B.反之,亦然.例1 设A={x | x是等腰三角形},B={x | x是直角三角形},则A∩B={等腰直角三角形} 例题Φ{斜三角形}A∪B={等腰三角形或直角三角形} 例3 设A={x -1< x < 2},B={x 1< x<3},求A∪B , A∩B. 例题AB 例题 练习 2. 已知集合A={x |-2≤x≤4}, B={x | x>a}
①若A∩B≠φ,求实数a的取值范围;
②若A∩B≠A,求实数a的取值范围.x=3, y = ,A∪ B={2,-1,7,-4}① a<4 ②a≥-21. 理解两个集合交集与并集的概念和性质. 2. 求两个集合的交集与并集,常用 数轴法 和图示法.有关不等式的解集的运算问题一般用数轴法。 课堂小结
1.正确理解并集与交集的概念。
2.会求两个已知集合的并集与交集。
3.通过韦恩图、数轴的利用,提高运用数形结合解决问题的能力。
教学重点:
并集、交集的概念,数形结合思想。
教学难点:
理解并集与交集的概念、符号之间的区别与联系.
教学方法:
发现式教学法必修①总第 4 课时复习引入1.子集、真子集的概念是怎样的? 2.子集、真子集有哪些性质? 集合间的基本运算(一)3.两个实数可以进行加、减、乘、除四则运算,那么两个集合是否也可以进行某种运算呢? 一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,记作 A∪B ,即A∪B={x | x∈A,或x∈B} 读作 A并 B 定义:并集观察集合A,B,C元素间的关系: A={4,5,6,8}, B={3,5,7,8},
C={3,4,5,6,7,8} 思考ABA∪B用Venn图表示如下: 一般地,由属于集合A且属于集合B的所有元素组成的集合叫做A与B的交集,即A∩B={x | x∈A,且x∈B} 读作 A交 B 定义:交集观察集合A,B,C元素间的关系: A={4,5,6,8}, B={3,5,7,8},
C={5,8} 思考记作 A∩B,ABA∩B用Venn图表示如下:(1) A∩A = A∩φ = (2) A∪A = A∪φ =AAφA==A∪B B∪AA∩B B∩A(3) A∩B A A∩B B(4) A A∪B B A∪B 性质⑸ 若A∩B=A,则A B.反之,亦然.⑹ 若A∪B=A,则A B.反之,亦然.例1 设A={x | x是等腰三角形},B={x | x是直角三角形},则A∩B={等腰直角三角形} 例题Φ{斜三角形}A∪B={等腰三角形或直角三角形} 例3 设A={x -1< x < 2},B={x 1< x<3},求A∪B , A∩B. 例题AB 例题 练习 2. 已知集合A={x |-2≤x≤4}, B={x | x>a}
①若A∩B≠φ,求实数a的取值范围;
②若A∩B≠A,求实数a的取值范围.x=3, y = ,A∪ B={2,-1,7,-4}① a<4 ②a≥-21. 理解两个集合交集与并集的概念和性质. 2. 求两个集合的交集与并集,常用 数轴法 和图示法.有关不等式的解集的运算问题一般用数轴法。 课堂小结
