1.1.3 集合的基本运算(1)
文档属性
| 名称 | 1.1.3 集合的基本运算(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 84.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-10 00:00:00 | ||
图片预览





文档简介
课件16张PPT。1.1.3 集合的基本运算(1)观察集合A,B,C元素间的关系:(1) A={4,5,6,8},B={3,5,7,8},
C={3,4,5,6,7,8}(2) A={x|x是有理数},B={x|x是无理数},
C={x|x是实数}1.通过上述问题中集合A与B与集合C之间的关系,类比
实数的加法运算,你发现了什么?提出问题:集合之间也可以相加,也可以进行运算,但是为了
不和实数的运算相混淆,规定这种运算不叫集合的加法
,而是叫做求集合的并集。集合C叫集合A与B的并集,
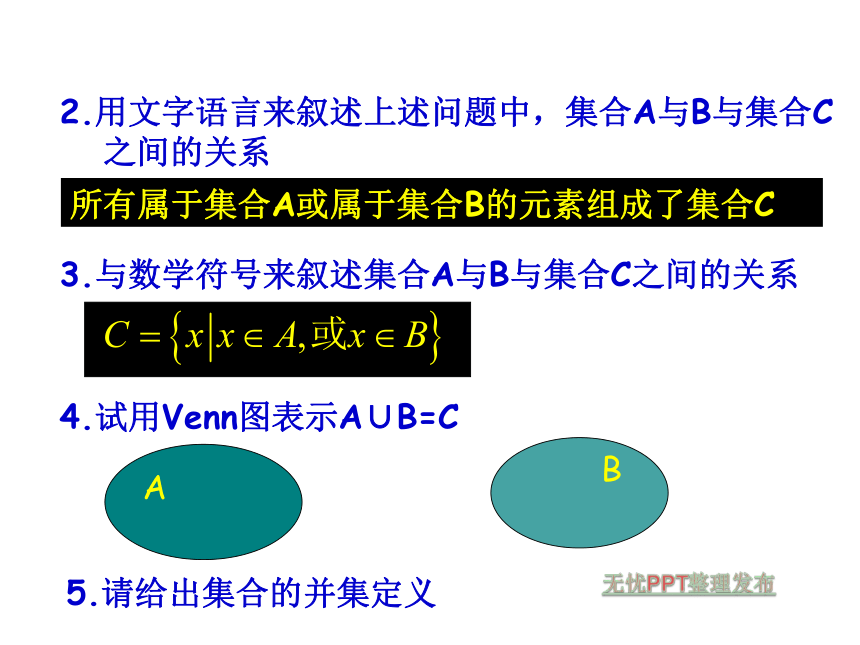
记为A∪B=C,读作A并B.3.与数学符号来叙述集合A与B与集合C之间的关系4.试用Venn图表示A∪B=C5.请给出集合的并集定义2.用文字语言来叙述上述问题中,集合A与B与集合C
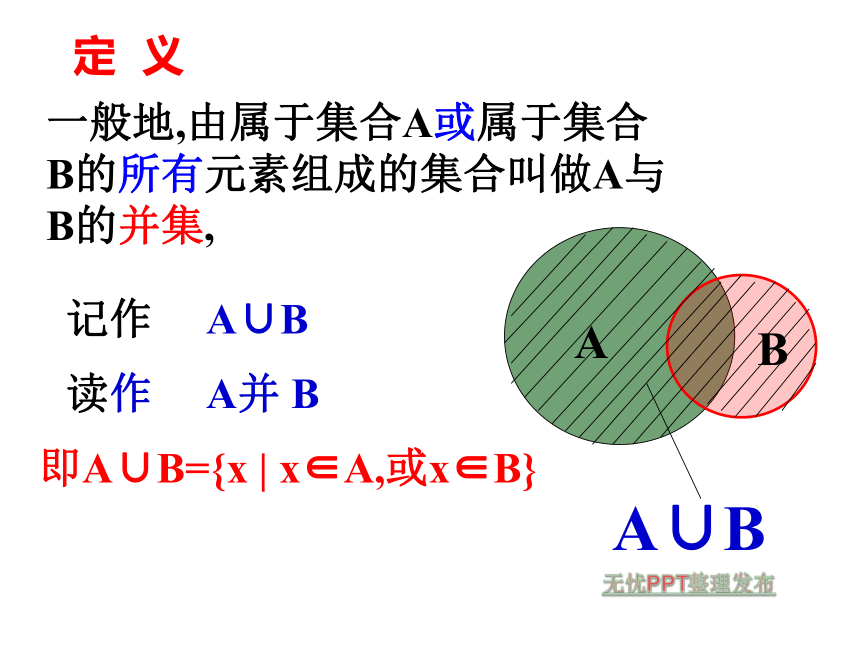
之间的关系所有属于集合A或属于集合B的元素组成了集合CA定 义一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,记作 A∪B即A∪B={x | x∈A,或x∈B} 读作 A并 BA∪B例1. A={4,5,6,8},B={3,5,7,8},求A∪B.例2.设A={x|-1 之间的关系2.与数学符号来叙述集合A与B与集合C之间的关系3.试用Venn图表示A∩B=C4.请给出集合的交集定义提出问题:定 义一般地,由既属于集合A又属于集合B的所有元素组成的集合叫做A与B的交集.记作 A∩B 即 A∩B={x |x∈A,且x∈B} 读作 A交 BA∩B应用示例例3.新华中学开运动会,设A={x|x是新华中学高一年级
参加百米赛跑的同学},B={x|x是新华中学高一年级
参加跳高比赛的同学},求A∩B .例4. 设平面内直线l1上点的集合为L1,直线l2上点的集合
为L2,用集合的运算表示l1、l2的位置关系.性 质2 A∩A = A∩φ = Aφ=A∩B B∩A抢答题课堂小结1. 理解两个集合交集与并集的概念bb和性质. 2. 求两个集合的交集与并集,常用 bbb数轴法和图示法.4. 注意对字母要进行讨论 . 3.注意灵活、准确地运用性质解题;2.教材P12 A组6,7,8 B组3作业布置1.教材P11练习T1~3.
C={3,4,5,6,7,8}(2) A={x|x是有理数},B={x|x是无理数},
C={x|x是实数}1.通过上述问题中集合A与B与集合C之间的关系,类比
实数的加法运算,你发现了什么?提出问题:集合之间也可以相加,也可以进行运算,但是为了
不和实数的运算相混淆,规定这种运算不叫集合的加法
,而是叫做求集合的并集。集合C叫集合A与B的并集,
记为A∪B=C,读作A并B.3.与数学符号来叙述集合A与B与集合C之间的关系4.试用Venn图表示A∪B=C5.请给出集合的并集定义2.用文字语言来叙述上述问题中,集合A与B与集合C
之间的关系所有属于集合A或属于集合B的元素组成了集合CA定 义一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,记作 A∪B即A∪B={x | x∈A,或x∈B} 读作 A并 BA∪B例1. A={4,5,6,8},B={3,5,7,8},求A∪B.例2.设A={x|-1
参加百米赛跑的同学},B={x|x是新华中学高一年级
参加跳高比赛的同学},求A∩B .例4. 设平面内直线l1上点的集合为L1,直线l2上点的集合
为L2,用集合的运算表示l1、l2的位置关系.性 质2 A∩A = A∩φ = Aφ=A∩B B∩A抢答题课堂小结1. 理解两个集合交集与并集的概念bb和性质. 2. 求两个集合的交集与并集,常用 bbb数轴法和图示法.4. 注意对字母要进行讨论 . 3.注意灵活、准确地运用性质解题;2.教材P12 A组6,7,8 B组3作业布置1.教材P11练习T1~3.
