1.1.3集合的基本运算

课件57张PPT。1．1.3　集合的基本运算 1．一般地，由所有属于集合A 属于集合B的元素所组成的集合叫做A与B的并集，记作 ，用描述法表示为 ．
(1)设A＝{1,2}，B＝{2,3,4}，则A∪B＝ ．
(2)设A＝{1,2}，B＝{a,3}，若A∪B＝{1,2,3}，
则a＝ ；若A∪B＝{1,2,3,4}，则a＝ .
(3)设A＝{x|x<1}，B＝{x|x<－1}，则A∪B＝ ．
(4)设A＝{x|x<－1}，B＝{x|x>－2}，则A∪B＝ .
(5)设A＝{x|x<－1}，B＝{x|x>1}，
则A∪B＝ ．或A∪B{x|x∈A或x∈B}{1,2,3,4}1或24{x|x<1}R{x|x<－1或x>1}2．一般地，由所有属于集合A 属于集合B的所有元素组成的集合叫做A与B的交集，记作 ，用描述法表示为 ．
用Venn图表示为 .
(1)设A＝{1,2}，B＝{2,3,4}，则A∩B＝ ．
(2)设A＝{x|x<1}，B＝{x|x>2}，则A∩B＝ .且A∩B{x|x∈A且x∈B}{2}?D (4)设A＝{1,2}，B＝{a,3}，若A∩B＝{1}，则a＝ ；若A∩B≠?，则a＝ .
(5)设A＝{x|x>－1}，B＝{x|x<－2}，则A∩B＝ .
3．(1)A∩A＝ ，A∪A＝ ，A∩?＝ ，
A∪?＝ .A∩B B∩A，A∪B B∪A.
(A∩B)∩C＝A∩(B∩C)，
(A∪B)∪C＝A∪(B∪C)．
A∩B?A，A∩B?B，A?A∪B，B?A∪B.11或2?AA?A＝＝(2)A?B?A∩B＝ ?A∪B＝ .
A∩B＝A∪B?A B，A∪B＝??A＝B＝ .
*(3)A∩(B∪C)＝(A∩B)∪(A∩C)
A∪(B∩C)＝(A∪B)∩(A∪C)．
4．设A＝{3,5,6,8}，B＝{4,5,7,8}，则
A∩B＝ ，A∪B＝ ．
5．(2010·湖南文，9)已知集合A＝{1,2,3}，B＝{2，m,4}，A∩B＝{2,3}，则m＝________.
[解析]　由题意知m＝3.
[答案]　3AB＝?{5,8}{3,4,5,6,7,8}6．(09·上海文)已知集合A＝{x|x≤1}，B＝{x|x≥a}，且A∪B＝R，则实数a的取值范围是________．
[答案]　a≤1
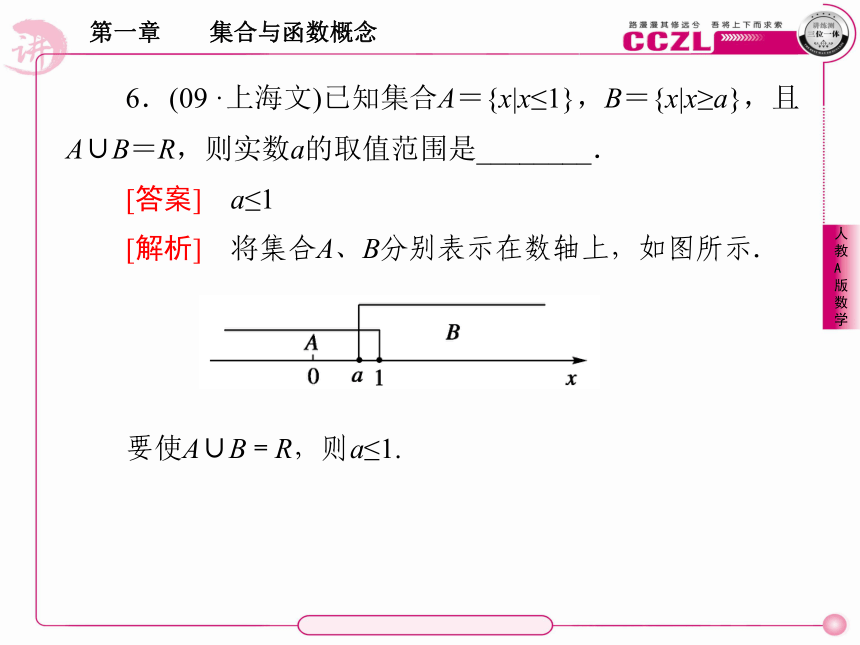
[解析]　将集合A、B分别表示在数轴上，如图所示．
要使A∪B＝R，则a≤1.7．你会求解下列问题吗？
集合A＝{x|－2≤x<1}．
(1)若B＝{x|x>m}，A?B，则m的取值范围是 .
(2)若B＝{x|x(3)若B＝{x|x本节难点：弄清交集与并集的概念及符号之间的联系和区别．1．正确理解和区分集合的“交”、“并”运算：
①A与B的交集是由A与B的所有的公共元素组成的集合．当两个集合A与B无公共元素时，A∩B＝?.
A与B的并集是由A的所有元素和B的所有元素组成的集合，当两个集合有公共元素时，公共元素在A∪B中只能出现一次．
②要注意“且”与“或”的含义，注意“且”与“或”和“交”与“并”分别对应．2．利用数形结合的思想，将满足条件的集合用韦恩图或数轴一一表示出来，从而求集合的交集、并集，这是既简单又直观且是最基本、最常见的方法，要注意灵活运用．
3．集合元素的互异性在解决集合的相等关系、子集关系、交集等时常遇到，忽视它很多时候会造成结果失误，解题时要多留意．
解决集合问题时，常常要分类讨论，要注意划分标准的掌握，做到不重、不漏，注意检验．
若已知x∈A∪B，那么它包含三种情形：
①x∈A且x?B；
②x∈B且x?A；
③x∈A且x∈B，这在解决与并集有关问题时应引起注意．[例1]　(1)若A＝{－1,1,3}，B＝{－2,1,2,3}，求A∪B.
(2)设A＝{x|－1[分析]　(1)由并集的定义求解．(2)结合数轴求解．
[解析]　(1)A∪B＝{－2，－1,1,2,3}．
(2)A∪B＝{x|－1＝{x|－1(1)已知集合A＝{x|x2－16＝0}，B＝{x|x2－x－12＝0}，则A∪B＝________.
(2)设A＝{x|x是锐角三角形}，B＝{x|x是钝角三角形}，则A∪B＝________.
[答案]　(1){－3,4，－4}(2){x|x是斜三角形}
[解析]　(1)∵A＝{4，－4}，B＝{－3,4}，
∴A∪B＝{－3,4，－4}
(2)A∪B＝{x|x是锐角三角形}∪{x|x是钝角三角形}＝{x|x是斜三角形}.
在求A∩B时，只要搞清两集合的公共元素是什么或公共元素具有怎样的性质即可．反之，若已知a∈A∩B，那么就可以断定a∈A且a∈B；若A∩B＝?，说明集合A与B没有公共元素．[例2]　(09·全国Ⅱ文)设集合M＝{m∈Z|－3(　　)
A．{0,1}　　　 B．{－1,0,1}
C．{0,1,2} D．{－1,0,1,2}
[解析]　∵M＝{－2，－1,0,1}，N＝{－1,0,1,2,3}，∴M∩N＝{－1,0,1}，故选B.
若集合A＝{x|－2≤x≤3}，B＝{x|x<－1或x>4}，则集合A∩B等于
(　　)
A．{x|x≤3或x>4} B．{x|－1C．{x|3≤x<4} D．{x|－2≤x<－1}
[答案]　D
[解析]　将集合A、B表示在数轴上，由数轴可得A∩B＝{x|－2≤x<－1}，故选D.[例3]　已知A＝{(x，y)|4x＋y＝6}，B＝{(x，y)|3x＋2y＝7}，则A∩B＝________.
已知A＝{x|x是等腰三角形}，B＝{x|x是直角三角形}，则A∩B＝________.
[答案]　{x|x是等腰直角三角形}
[解析]　A∩B＝{x|x是等腰三角形}∩{x|x是直角三角形}
＝{x|x是等腰直角三角形}.
[例4]　已知集合A＝{x|1≤x＜3}，B＝{x|x＞2}，试求A∩B和A∪B.
[分析]　借助于数轴直观解题．
[解析]　根据A∩B、A∪B的定义，借助图形可知．
A∩B＝{x|2＜x＜3}，A∪B＝{x|x≥1}． 总结评述：要注意A∩B与A∪B的区别与联系，特别注意端点位置的数是否在其中．
设集合A＝{x|1≤x<3}，B＝{x|x>a}．
(1)若A?B，则a的取值范围是________；
(2)若A∩B≠?，则a的取值范围是________；
(3)若A∪B＝B，则a的取值范围是________；
(4)求A∩B＝A，则a的取值范围是________．
[答案]　(1)a<1　(2)a<3　(3)a<1　(4)a<1[解析]　借助数轴讨论，注意端点能否取到．[例5]　已知集合A＝{－4,2a－1，a2}，B＝{a－5，1－a，9}，分别求适合下列条件的a值．
(1)9∈A∩B；
(2){9}＝A∩B.
[分析]　9∈A∩B与{9}＝A∩B意义不同，9∈A∩B说明9是A与B的一个公共元素，但A与B中允许有其它公共元素．
{9}＝A∩B，说明A与B的公共元素有且只有一个9.[解析]　(1)∵9∈A∩B，∴9∈A
∴2a－1＝9或a2＝9，∴a＝5或a＝±3.
检验知：a＝5或a＝－3满足题意．
(2)∵{9}＝A∩B，∴9∈A∩B，
∴a＝5或a＝±3.检验知：a＝5时，A∩B＝{－4,9}不合题意，∴a＝－3. 总结评述：(1)中检验的是集合A、B中的元素是否是互异的，a＝3时，B中元素a－5与1－a相同，所以a＝3应舍去；(2)中进一步检验A与B有没有不是9的公共元素，a＝5时，A＝{－4,9,25}，B＝{0，－4,9}，这时A∩B＝{－4,9}≠{9}，所以a＝5应舍去．
已知：A＝{x|2x2－ax＋b＝0}，B＝{x|bx2＋(a＋2)x＋5＋b＝0}，且A∩B＝{ }，求A∪B.
[例6]　高一(3)班的学生中，参加语文课外小组的有20人，参加数学课外小组的有22人，既参加语文又参加数学小组的有10人，既未参加语文又未参加数学小组的有15人，问高一(3)班共有学生几人？
[分析]　借助Venn图可直观地得出有限集元素的个数．用card(A)表示集合A中所含元素的个数，则计数公式card(A∪B)＝card(A)＋card(B)－Card(A∩B)[解析]　设U＝{高一(3)班学生}，A＝{高一(3)班参加语文小组的学生}，B＝{高一(3)班参加数学小组的学生}，则A∩B＝{高一(3)班既参加语文小组又参加数学小组的学生}．
有card(U)＝15＋card(A∪B)＝15＋card(A)＋card(B)－card(A∩B)＝15＋20＋22－10＝47(人)．故高一(3)班有47名学生．
50名学生报名参加A、B两项课外活动小组，报名参加A组的人数是全体学生数的五分之三，报名参加B组的人数比报名参加A组的人数多3人，两组都没报名的人数比同时报名参加A、B两组人数的三分之一多1人．求同时报名参加两组的人数．[例7]　设集合A＝{y∈R|y＝x2＋1，x∈R}，B＝{y∈R|y＝x＋1，x∈R}，则A∩B＝
(　　)
A．{(0,1)，(1,2)}　 　　 B．{(0,1)}
C．{(1,2)} D．{y∈R|y≥1}[辨析]　以上解法不对．集合A，B应该结合代表元素从整体意义上把握，它们是当x取一切实数时所得的y的值的集合，在审题时必须首先弄清集合的本质含义．
[正解]　A＝{y∈R|y≥1}，B＝R，故A∩B＝{y∈R|y≥1}，正确答案为D.一、选择题
1．若集合M＝{(x，y)|x＋y＝0}，P＝{(x，y)|x－y＝2}，则M∩P等于
(　　)
A．(1，－1) B．{x＝1或y＝1}
C．{1，－1} D．{(1，－1)}
[答案]　D2．设集合A＝{x|－1≤x≤2}，集合B＝{x|x≤a}，若A∩B＝?，则实数a的取值集合为
(　　)
A．{a|a<2} B．{a|a≥－1}
C．{a|a<－1} D．{a|－1≤a≤2}
[答案]　C
[解析]　如图．
要使A∩B＝?，应有a<－1.3．(09·辽宁文)已知集合M＝{x|－35}，则M∪N＝
(　　)
A．{x|x<－5或x>－3}
B．{x|－5C．{x|－3D．{x|x<－3或x>5}
[答案]　A
[解析]　在数轴上分别表示出集合A、B，观察得出答案．4．(09·广东理)已知全集U＝R，集合M＝{x|－2≤x－1≤2}和N＝{x|x＝2k－1，k＝1,2，…}的关系的韦恩(Venn)图如图所示，则阴影部分所示的集合的元素共有
(　　)
A．3个 B．2个
C．1个 D．无穷多个[答案]　B
[解析]　M＝{x|－1≤x≤3}，N为正奇数集，
∴M∩N＝{1,3}．
二、填空题
5．A＝{x∈N*|4[答案]　{3,5,6,7}
[解析]　解A＝{5,6,7}，B＝{3,5}，∴A∪B＝{3,5,6,7}．6．若A＝{x|a≤x≤1}，则B＝{x|x≤b}，A∩B＝{x|－2≤x≤1}，A∪B＝{x|x≤2}，则a＋b＝________.
[答案]　0
[解析]　由A∩B知a＝－2，由A∪B知b＝2，∴a＋b＝0.7．(09·湖南文)某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为______．
[答案]　12
[解析]　如图，全班同学组成集合U，喜欢篮球的组成集合A，喜欢乒乓球运动的组成集合B，则A∩B中人数为：15＋10＋8－30＝3人，∴喜欢篮球不喜欢乒乓球运动的人数为15－3＝12人．8．定义集合运算A*B＝{z|z＝xy，x∈A，y∈B}，若A＝{1,2}，B＝{0,3}，则集合A*B中所有元素之和为________．
[答案]　9
[解析]　由A*B的定义知，A*B＝{0,3,6}，
所有元素的和为9.三、解答题
9．已知：A＝{x||x－a|＜4}，B＝{x|x＜－1或x≥5}，且A∪B＝R，求实数a的范围．*10.已知集合P＝{x|－3＜x＜－2，或x＞1}，M＝{x|a≤x≤b}，且P∪M＝{x|x＞－3}，P∩M＝{x|1＜x≤3}，求实数a、b的值．