1-2-1函数的概念 (2)
图片预览











文档简介
课件66张PPT。1.2 函数及其表示1.2.1 函数的概念1.设在一个变化过程中有两个变量x,y,如果对于x的每一个值,y都有 确定的值与它对应,那么就说y是x的函数,x叫做自变量.唯一答案:(1)是 (2)不是 3.下面我们用集合与对应的观点来研究函数,先阅读教材P15~16,再回答问题.
设A、B是 ,如果按照某种确定的对应关系f,使对于集合A中的 ,在集合B中都有 确定的数f(x)和它对应,那么就称f:A→B为集合A到集合B的一个函数.记作 ,其中x叫做 , 叫做函数的定义域,与x的值相对应的y值叫做
,函数值的集合 叫做函数的值域.非空数集任意一个数x唯一y=f(x)自变量A函数值{y|y=f(x),x∈A}4.函数的定义域是使函数有意义的自变量x的取值集合,值域是函数值的集合.
(1)一次函数y=kx+b(k≠0)的定义域为 ;
值域为 .RR(5)当函数是由实际问题给出时,其定义域不仅要考虑使其解析式有意义,还要有实际意义;
一种练习本的单价为0.6元,买本子的个数x与应付钱数y之间的函数关系为 ,其中x的允许取值范围是 .y=0.6xx∈N5.如果两个函数的定义域相同,并且对应关系完全一致,那么就称这两个函数相等.
(1)只要两个函数的定义域相同,对应法则相同,其值域就 .故判断两个函数是否相等时,一看定义域,二看对应法则.
如y=1与y= 不是相等函数,因为 .y=3t+4与y=3x+4是相等函数.
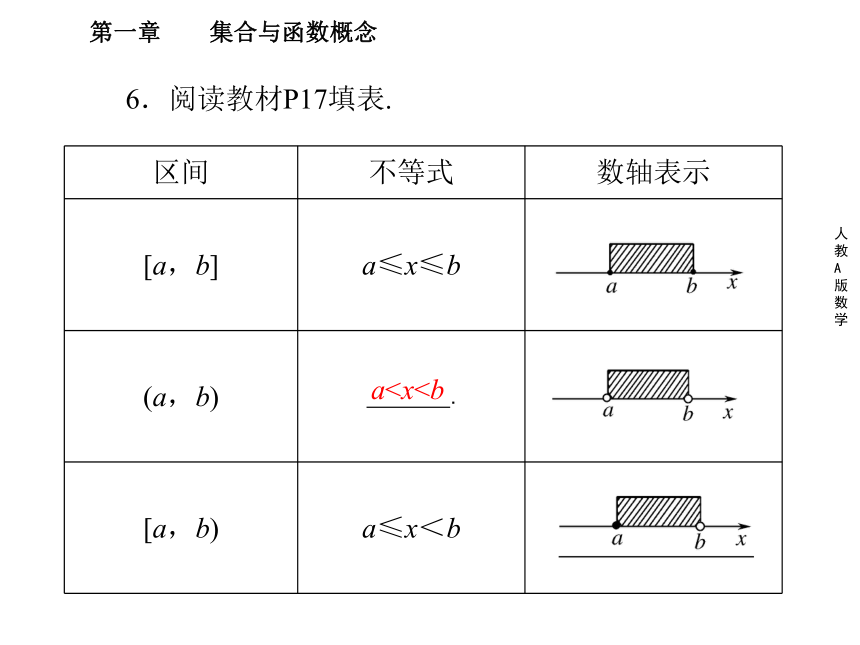
(2)求函数的定义域,一般是转化为解不等式或不等式组的问题,注意定义域是一个集合,其结果必须用集合或区间来表示.一定相同定义域不同6.阅读教材P17填表.a本节难点:(1)函数概念的理解.
(2)实际应用问题中函数的定义域和复合函数定义域.(一)对函数y=f(x)涵义的理解,应明确以下几点:
①“A,B是非空数集”,若求得自变量取值范围为?,则此函数不存在.
②定义域、对应法则和值域是函数的三要素,实际上,值域是由定义域和对应法则决定的,所以看两个函数是否相等,只要看这两个函数的定义域与对应法则是否相同.③y=f(x)中f为对应法则,当情况比较简单时,对应法则f可用一个解析式来表示.但在有些问题中,对应法则f也可能不便用或不能用一个解析式来表示,这时就必须采用其他方式,如数表或图象等.
④函数符号“y=f(x)”是“y是x的函数”的数学表示,仅仅是函数符号,不是表示“y等于f与x的乘积”,f(x)也不一定是解析式.符号f(a)与f(x)既有区别又有联系,f(a)表示当自变量x=a时函数f(x)的值,而f(x)是自变量x的函数.一般情况下,f(x)是一个变量,f(a)是f(x)的一个特殊值.(二)复合函数定义域的求法
已知f(x)定义域为A,求f(φ(x))定义域,应使φ(x)∈A;已知f(φ(x))定义域为A,求f(x)定义域,即求当x∈A时,φ(x)的值域.[分析] (1)据函数的定义:“对于集合A中的任意一个元素,在集合B中有唯一确定的元素与之对应”进行判断.
(2)给定函数的解析式,也就给定了由定义域到值域的对应法则,只要将自变量允许值代入,就可以求得对应的函数值. 总结评述:判断由一个式子是否能确定y是x的函数的程序是:对于由式子有意义所确定的x的取值集合中任一个x的值,由式子是否可确定唯一的一个y的值与之对应,也可以看由式子解出x的解析式是否唯一.
(1)已知集合A={1,2,3,4},B={5,6,7},在下列A到B的四种对应关系中,能确定A到B的函数关系的个数是
( )
A.1
B.2
C.3
D.4[解析] (1)①③能确定A到B的函数关系,它们都满足对于A中每一个元素,在B中有惟一元素与之对应.且A,B都是非空数集;②④都不能确定A到B的函数关系.②的集合A中元素4在B中无对应元素;④的集合A中元素3,在B中有两个元素与之对应,故选B.[分析] 确定两个函数是否相等,要紧紧抓住函数的定义域和对应法则.根据函数的定义可知,定义域中的每一个x都有唯一的y与它对应,所以值域实际上是由定义域和对应法则确定,因此,两个函数只要定义域和对应法则分别相同,它们就是相等函数.[解析] ①中f(x)=x+1,x∈R,而y=x+x0中x≠0,它们的定义域不相同,所以不是相等函数.
②中两个函数的定义域都是R,并且f(x)= =|2x+1|,所以它们是相等函数.
③中f(n)=2n+1(n∈Z)与g(n)=2n-1(n∈Z)的定义域都是Z,值域也相同(都是奇数集),但对应法则不同,所以不是相等函数.
④中f(x)=3x+2与g(t)=3t+2的定义域都是R,尽管它们表示自变量的字母不同,但是,对应法则都是“乘3加2”,是相同的对应法则,所以是相等函数.
故填②④. 总结评述:从函数的概念可知,函数有定义域、值域、对应法则三要素,其中,定义域是前提,对应法则是核心,值域是由定义域和对应法则确定的.因此,
1)当两个函数的定义域不同或对应法则不同,它们就不是同一个函数.只有当定义域和对应法则都相同时它们才是相等函数.
2)对应法则f是函数关系的本质特征,要深刻理解,准确把握,它的核心是“法则”.通俗地说,就是给出了一个自变量后的一种“算法”,至于这个自变量是用x还是用t或者别的符号表示,那不是“法则”的本质,因此,对应法则与自变量所用的符号无关.3)从本题我们也得到这样的启示:在对函数关系变形或化简时,一定要注意使函数的定义域保持不变,否则,就变成了不同的函数.这也正说明了函数的定义域是函数不可忽视的一个重要组成部分.例如f(x)=x2-x (x≥1),f(3)=32-3=6,但f(-1)是无意义的,不能得出f(-1)=(-1)2-(-1)=2,因为只有当x取定义域[1,+∞)内的值时,才能按这个法则x2-x进行计算.[解析] ①要使函数有意义,只要-x2+5x-6>0,即-(x-2)(x-3)>0,∴2<x<3.
故函数的定义域为{x|2<x<3}.[答案] {x∈R且x≠-1,x≠-2}
[例4] 某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
周长为l的铁丝弯成下部为矩形,上部为半圆形的框架(如右图所示).若矩形底边长为2x,求此框架围成图形的面积y关于x的函数,并求出定义域.
[例5] 设y=f(x)的定义域是[0,2],求下列函数的定义域.
(1)f(x+3);(2)f(|2x-1|);(3)f(x+a)-f(x-a)(0[分析] 根据“若f(x)的定义域为[a,b],则f[g(x)]的定义域为a≤g(x)≤b的解集”来解相应的不等式(或不等式组).
已知y=f(x+1)的定义域为[0,1].则y=f(x)的定义域为________.
[解析] 由题设使y=f(x+1)有意义的x允许取值范围是0≤x≤1.∴1≤x+1≤2
∴欲使y=f(x)有意义,须1≤x≤2.
∴此函数的定义域为[1,2].[分析] 因为函数y=f(x),当x在函数的定义域内时f(x)都有意义,又f(x·y)-f(x)=f(y)对任意实数x,y(xy≠0)都成立,故只要取某些特殊值即可得证.[点评] 由于函数f(x)对任意非零实数x、y都有f(xy)-f(x)=f(y)成立.因此当x、y取某些特殊值时一定成立,故解决这类问题可用赋值法,通过赋值产生已知条件式和待求解的结论式使之建立联系.[例7] 某农户计划建筑一矩形羊圈,现有可作为围墙的材料总长度为100米,求羊圈的面积S与长x的函数关系式.
[错解] 设羊圈的长为x米,则宽为(50-x)米,由题意得,S=x(50-x),
故函数关系式为S=x(50-x).
[辨析] 解题到此为止,则本题的函数关系式还不完整,缺少自变量x的范围,也就是说解题思路不够严密.[正解] 设羊圈的长为x米,则宽为(50-x)米,由题意得,S=x(50-x),
因为羊圈的长和宽都不能小于等于零,也就是羊圈的面积应为正数,
故函数关系式为S=x(50-x) (01.给出下列从A到B的对应:
①A=N,B={0,1},对应关系是:A中的元素除以2所得的余数
②A={0,1,2},B={4,1,0},对应关系是f:x→y=x2
其中表示从集合A到集合B的函数有( )个.
( )
A.1 B.2 C.3 D.0[答案] B
[解析] 由于③中,0这个元素在B中无对应元素,故不是函数,因此选B.2.已知x∈A,y∈B,在以下的对应中,y不是x的函数的是(如下图)
( )[答案] A
[解析] 在A图中,集合A中元素1在集合B中有两个元素1和-1与之对应,故y不是x的函数.3.下列各图中,不可能表示函数y=f(x)的图象的是
( )[答案] B
[解析] B图中,作垂直于x轴的直线,与图形可以有两个交点,故存在x,有两个y值与之对应,故B图y不是x的函数.4.A={x|0≤x≤2},B={y|1≤y≤2},下列图形中能表示以A为定义域,B为值域的函数的是
( )[答案] B
[解析] A、C、D的值域都不是[1,2],故选B.
5.某种细胞分裂时,每次分裂由1个分裂为2个,2个分裂为4个……一个这样的细胞分裂x次后,得到的细胞的个数y与x的函数关系式为
( )
A.y=2x B.y=2x
C.y=4x D.y=x4
[答案] B[答案] A
设A、B是 ,如果按照某种确定的对应关系f,使对于集合A中的 ,在集合B中都有 确定的数f(x)和它对应,那么就称f:A→B为集合A到集合B的一个函数.记作 ,其中x叫做 , 叫做函数的定义域,与x的值相对应的y值叫做
,函数值的集合 叫做函数的值域.非空数集任意一个数x唯一y=f(x)自变量A函数值{y|y=f(x),x∈A}4.函数的定义域是使函数有意义的自变量x的取值集合,值域是函数值的集合.
(1)一次函数y=kx+b(k≠0)的定义域为 ;
值域为 .RR(5)当函数是由实际问题给出时,其定义域不仅要考虑使其解析式有意义,还要有实际意义;
一种练习本的单价为0.6元,买本子的个数x与应付钱数y之间的函数关系为 ,其中x的允许取值范围是 .y=0.6xx∈N5.如果两个函数的定义域相同,并且对应关系完全一致,那么就称这两个函数相等.
(1)只要两个函数的定义域相同,对应法则相同,其值域就 .故判断两个函数是否相等时,一看定义域,二看对应法则.
如y=1与y= 不是相等函数,因为 .y=3t+4与y=3x+4是相等函数.
(2)求函数的定义域,一般是转化为解不等式或不等式组的问题,注意定义域是一个集合,其结果必须用集合或区间来表示.一定相同定义域不同6.阅读教材P17填表.a
(2)实际应用问题中函数的定义域和复合函数定义域.(一)对函数y=f(x)涵义的理解,应明确以下几点:
①“A,B是非空数集”,若求得自变量取值范围为?,则此函数不存在.
②定义域、对应法则和值域是函数的三要素,实际上,值域是由定义域和对应法则决定的,所以看两个函数是否相等,只要看这两个函数的定义域与对应法则是否相同.③y=f(x)中f为对应法则,当情况比较简单时,对应法则f可用一个解析式来表示.但在有些问题中,对应法则f也可能不便用或不能用一个解析式来表示,这时就必须采用其他方式,如数表或图象等.
④函数符号“y=f(x)”是“y是x的函数”的数学表示,仅仅是函数符号,不是表示“y等于f与x的乘积”,f(x)也不一定是解析式.符号f(a)与f(x)既有区别又有联系,f(a)表示当自变量x=a时函数f(x)的值,而f(x)是自变量x的函数.一般情况下,f(x)是一个变量,f(a)是f(x)的一个特殊值.(二)复合函数定义域的求法
已知f(x)定义域为A,求f(φ(x))定义域,应使φ(x)∈A;已知f(φ(x))定义域为A,求f(x)定义域,即求当x∈A时,φ(x)的值域.[分析] (1)据函数的定义:“对于集合A中的任意一个元素,在集合B中有唯一确定的元素与之对应”进行判断.
(2)给定函数的解析式,也就给定了由定义域到值域的对应法则,只要将自变量允许值代入,就可以求得对应的函数值. 总结评述:判断由一个式子是否能确定y是x的函数的程序是:对于由式子有意义所确定的x的取值集合中任一个x的值,由式子是否可确定唯一的一个y的值与之对应,也可以看由式子解出x的解析式是否唯一.
(1)已知集合A={1,2,3,4},B={5,6,7},在下列A到B的四种对应关系中,能确定A到B的函数关系的个数是
( )
A.1
B.2
C.3
D.4[解析] (1)①③能确定A到B的函数关系,它们都满足对于A中每一个元素,在B中有惟一元素与之对应.且A,B都是非空数集;②④都不能确定A到B的函数关系.②的集合A中元素4在B中无对应元素;④的集合A中元素3,在B中有两个元素与之对应,故选B.[分析] 确定两个函数是否相等,要紧紧抓住函数的定义域和对应法则.根据函数的定义可知,定义域中的每一个x都有唯一的y与它对应,所以值域实际上是由定义域和对应法则确定,因此,两个函数只要定义域和对应法则分别相同,它们就是相等函数.[解析] ①中f(x)=x+1,x∈R,而y=x+x0中x≠0,它们的定义域不相同,所以不是相等函数.
②中两个函数的定义域都是R,并且f(x)= =|2x+1|,所以它们是相等函数.
③中f(n)=2n+1(n∈Z)与g(n)=2n-1(n∈Z)的定义域都是Z,值域也相同(都是奇数集),但对应法则不同,所以不是相等函数.
④中f(x)=3x+2与g(t)=3t+2的定义域都是R,尽管它们表示自变量的字母不同,但是,对应法则都是“乘3加2”,是相同的对应法则,所以是相等函数.
故填②④. 总结评述:从函数的概念可知,函数有定义域、值域、对应法则三要素,其中,定义域是前提,对应法则是核心,值域是由定义域和对应法则确定的.因此,
1)当两个函数的定义域不同或对应法则不同,它们就不是同一个函数.只有当定义域和对应法则都相同时它们才是相等函数.
2)对应法则f是函数关系的本质特征,要深刻理解,准确把握,它的核心是“法则”.通俗地说,就是给出了一个自变量后的一种“算法”,至于这个自变量是用x还是用t或者别的符号表示,那不是“法则”的本质,因此,对应法则与自变量所用的符号无关.3)从本题我们也得到这样的启示:在对函数关系变形或化简时,一定要注意使函数的定义域保持不变,否则,就变成了不同的函数.这也正说明了函数的定义域是函数不可忽视的一个重要组成部分.例如f(x)=x2-x (x≥1),f(3)=32-3=6,但f(-1)是无意义的,不能得出f(-1)=(-1)2-(-1)=2,因为只有当x取定义域[1,+∞)内的值时,才能按这个法则x2-x进行计算.[解析] ①要使函数有意义,只要-x2+5x-6>0,即-(x-2)(x-3)>0,∴2<x<3.
故函数的定义域为{x|2<x<3}.[答案] {x∈R且x≠-1,x≠-2}
[例4] 某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
周长为l的铁丝弯成下部为矩形,上部为半圆形的框架(如右图所示).若矩形底边长为2x,求此框架围成图形的面积y关于x的函数,并求出定义域.
[例5] 设y=f(x)的定义域是[0,2],求下列函数的定义域.
(1)f(x+3);(2)f(|2x-1|);(3)f(x+a)-f(x-a)(0
已知y=f(x+1)的定义域为[0,1].则y=f(x)的定义域为________.
[解析] 由题设使y=f(x+1)有意义的x允许取值范围是0≤x≤1.∴1≤x+1≤2
∴欲使y=f(x)有意义,须1≤x≤2.
∴此函数的定义域为[1,2].[分析] 因为函数y=f(x),当x在函数的定义域内时f(x)都有意义,又f(x·y)-f(x)=f(y)对任意实数x,y(xy≠0)都成立,故只要取某些特殊值即可得证.[点评] 由于函数f(x)对任意非零实数x、y都有f(xy)-f(x)=f(y)成立.因此当x、y取某些特殊值时一定成立,故解决这类问题可用赋值法,通过赋值产生已知条件式和待求解的结论式使之建立联系.[例7] 某农户计划建筑一矩形羊圈,现有可作为围墙的材料总长度为100米,求羊圈的面积S与长x的函数关系式.
[错解] 设羊圈的长为x米,则宽为(50-x)米,由题意得,S=x(50-x),
故函数关系式为S=x(50-x).
[辨析] 解题到此为止,则本题的函数关系式还不完整,缺少自变量x的范围,也就是说解题思路不够严密.[正解] 设羊圈的长为x米,则宽为(50-x)米,由题意得,S=x(50-x),
因为羊圈的长和宽都不能小于等于零,也就是羊圈的面积应为正数,
故函数关系式为S=x(50-x) (0
①A=N,B={0,1},对应关系是:A中的元素除以2所得的余数
②A={0,1,2},B={4,1,0},对应关系是f:x→y=x2
其中表示从集合A到集合B的函数有( )个.
( )
A.1 B.2 C.3 D.0[答案] B
[解析] 由于③中,0这个元素在B中无对应元素,故不是函数,因此选B.2.已知x∈A,y∈B,在以下的对应中,y不是x的函数的是(如下图)
( )[答案] A
[解析] 在A图中,集合A中元素1在集合B中有两个元素1和-1与之对应,故y不是x的函数.3.下列各图中,不可能表示函数y=f(x)的图象的是
( )[答案] B
[解析] B图中,作垂直于x轴的直线,与图形可以有两个交点,故存在x,有两个y值与之对应,故B图y不是x的函数.4.A={x|0≤x≤2},B={y|1≤y≤2},下列图形中能表示以A为定义域,B为值域的函数的是
( )[答案] B
[解析] A、C、D的值域都不是[1,2],故选B.
5.某种细胞分裂时,每次分裂由1个分裂为2个,2个分裂为4个……一个这样的细胞分裂x次后,得到的细胞的个数y与x的函数关系式为
( )
A.y=2x B.y=2x
C.y=4x D.y=x4
[答案] B[答案] A
