1-2-2-2分段函数与映射
图片预览











文档简介
课件60张PPT。1.当自变量x在不同的取值区间(范围)内取值时,函数的对应法则也不同的函数为 .
分段函数是一个函数,不是几个函数,只是在定义域的不同范围上取值时对应法则不同,分段函数是普遍存在又比较重要的一种函数.
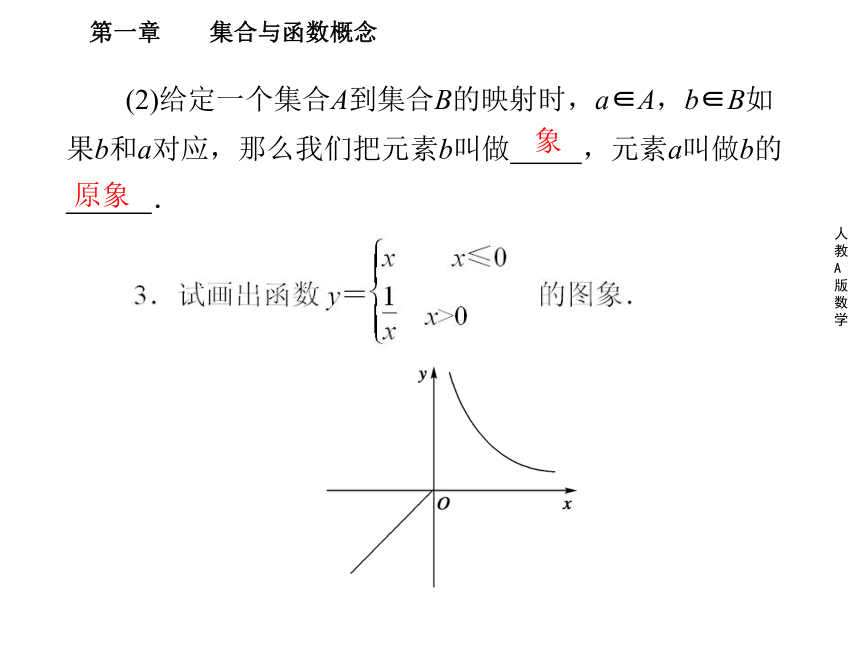
2.(1)设A、B是两个集合,如果按照某种对应关系f,对于集合A中的 一个元素,在集合B中有 确定的元素和它对应,那么这样的对应(包括A、B以及对应关系f)叫做集合A到B的映射,记作 .分段函数唯一任何f:A→B(2)给定一个集合A到集合B的映射时,a∈A,b∈B如果b和a对应,那么我们把元素b叫做 ,元素a叫做b的 .象原象本节重点:①分段函数概念的理解;②映射定义理解.
本节难点:①函数图象的画法;②分段函数的理解应用;③用映射理解函数的定义.(1)分段函数的定义域是各段自变量取值集合的并集;值域是各段函数值集合的并集;最大(小)值是各段上最大(小)值中的最大(小)者.研究分段函数常借助图象进行.
(2)映射f:A→B包含三个要素:原象集合A,象集合B(或B的子集)以及从集合A到集合B的对应法则f.两个集合A、B可以是数集,也可以是点集或其它集合.对应法则f可用文字表述,也可以用符号表示.映射是一种特殊的对应,它具有:①方向性:映射是有次序的,一般地从A到B的映射与从B到A的映射是不同的;
②任意性:集合A中的任意一个元素都有象,但不要求B中的每一个元素都有原象;
③唯一性:集合A中元素的象是唯一的,即不允许“一对多”但可以“多对一”.[分析] 图象法是表示函数的方法之一,画函数的图象时,以定义域、对应法则为依据,采用列表、描点法作图. 总结评述:函数的图象可以是一些线段,一段曲线,甚至是一些点.表示函数的式子也可以不止一个,这类用几个式子表示的函数叫做分段函数.分段函数是一个函数,而不是几个函数,必须分段画出函数图象,尤其需注意特殊点. [答案] B
[例2] 设f:M→N是集合M到集合N的映射,下列说法中正确的是
( )
A.M中每一个元素在N中必有元素与之对应
B.N中每一个元素在M中必有元素与之对应
C.M中的元素在N中可以有不同元素与之对应
D.N中的元素在M中若有原象,则原象必是惟一的
[分析] 根据映射的定义判断.[解析] 在映射中允许集合N中的某些元素在集合M中没有元素对应,所以B是错误的;又因为映射中允许集合M中不同元素对应集合N中相同的元素,就是说可以“多对一”,因此D也是错误的.M中元素的象是惟一的,故C错,∴选A.[答案] B
[分析] 判断两个集合之间的对应是否为映射,只要按照对应法则f判断,对于集合A中的任何一个元素,在集合B中是否有惟一的元素和它对应.[解析] 在A中,当x=3时,|x-3|=0,于是A中有一个元素在B中没有元素和它对应,故不是映射;在C中,集合A中的负数在B中没有元素和它对应,故也不是映射;(或者x>0时,B中对应元素不唯一);在D中,集合A中元素为0时,其倒数不存在,因而0在B中无对应元素,故同样不是映射;B符合定义,故选B.[例3] 已知集合A=B={(x,y)|x、y∈R},给定映射f:A→B,使得集合A中的元素(x,y)与集合B中的元素(x+y,xy)对应.
(1)求A中元素(-2,3)的象;
(2)求B中元素(2,-3)的原象;
*(3)判断集合A中是否存在元素与B中形如(a,a2)的元素对应;若存在,求之;若不存在,说明理由.
[分析] 由对应法则,可以根据A中元素与B中元素的对应关系建立起关于x、y的方程组.其中第(3)问即是判断相应的方程组是否有解,何时有解. 总结评述:在一个给定的映射f:A→B中,A中每一个元素在B中都有唯一元素与之对应,但B中元素在A中未必有元素对应,即A中元素对应B中元素的集合实际上是集合B的一个子集.在涉及元素的对应问题中,常常需要建立方程组求解.(2)设集合A、B都是正整数集,映射f:A→B把集合A中的元素n映射到集合B中的元素3n+2n,则在映射f下,象89的原象是
( )
A.2 B.3
C.4 D.5
[答案] (1)D (2)C[点评] (2)验证次数要尽可能的少,故先验证B,若n=3时,结果比89小,则排除A、B.若等于89,则知选B,若大于89,则选A.[分析] 这是已知分段函数的函数值求相应自变量的值的问题.一般从两个角度思考:一是先求各段上函数值的取值范围,再结合所给函数值的大小,确定在哪段上求解;二是逐段令其值为已知函数值解出x的值,看是否满足其取值范围的要求做出取舍.[答案] A
[例5] 上因特网的费用由两部分组成:电话费和上网费.以前某“热线”上因特网的费用为电话费0.12元/3分钟,上网费0.12元/分钟.根据信息产业部调整因特网资费的要求,自1999年3月1日起,该地区上因特网的费用调整为电话费0.16元/3分钟,上网费每月不超过60小时,以4元/时计算,超过60小时部分,以8元/时计算.(1)根据调整后的规定,将每月上因特网的费用表示为时间(小时)的函数(每月按30天计算);
(2)某网民在其家庭经济预算中一直有一笔上网60小时的费用开支,因特网资费调整后,若要不超过其家庭经济预算中上网费支出,则该网民现在每月可上网多少小时,从涨价和降价的角度分析该地区调整前后上因特网的费用情况.[解析] 设调整后上网x小时的费用为f(x)元.
(1)当0<x≤60时,f(x)=0.16×20x+4x=7.2x;
当x>60时,f(x)=4×60+0.16×20x+(x-60)×8=11.2x-240.(2)设调整前上网x小时的费用为g(x)元,则g(x)=0.12×20x+0.12×60x=9.6x.
原上网60小时预算费用为9.6×60=576(元),由576=11.2x-240得x≈72.85(时),故该网民现在每月可上网72.85小时.
当0<x≤60时,f(x)<g(x);
当x>60时,由f(x)=g(x),可得x=150.
所以,上网小于150小时时,f(x)<g(x);上网大于150小时时,f(x)>g(x).
如图,在边长为4的正方形ABCD的边上有一点P,沿折线BCDA由点B(起点)向点A(终点)运动,设点P运动的路程为x,△APB的面积为y.
(1)求y关于x的函数关系式y=f(x);
(2)画出y=f(x)的图象;
(3)若△APB的面积不小于2,
求x的取值范围.(2)y=f(x)的图象如图所示.
(3)即f(x)≥2,当0≤x≤4时,2x≥2,∴x≥1,
当8∴x≤11,∴x的取值范围是1≤x≤11.[点评] (3)可以作直线y=2与函数y=f(x)的图象交于点A(1,2),B(11,2),要使y≥2,应有1≤x≤11.[例6] 设集合A={1,2,3,k},B={4,7,a4,a2+3a},其中a,k∈N,映射f:A→B使B中的元素y与A中元素x对应且y=3x+1,求a及k的值.
[错解] ∵B中元素y=3x+1与A中元素x对应,∴A中元素1,2分别对应B中元素4,7.
∵a,k∈N,∴a不存在,∴k不存在.[辨析] 以上解法的错误之处在于误解了映射的定义.由于集合元素的无序性,所以a4=10或a2+3a=10都有可能,因而要分类讨论.一、选择题
1.函数y=|x+1|的图象是 ( )[答案] A
[解析] 当x=-1时y=0,因此否定B、C,又y≥0,否定D,故选A.2.在如图的对应关系中,哪些对应不是集合A到集合B的映射
( )
A.①、②
B.①、④
C.②、⑤
D.①、②、③[答案] D
[解析] 由图知①②中元素a1在B中对应元素不唯一,③中元素a2在B中无象,都不是映射,④⑤是映射,故选D.[答案] B
[解析] 设(x,y)在f作用下对应(3,1),则
∴与(3,1)对应的元素为(1,1),故选B.4.已知图①中的图象对应的函数为y=f(x),则图②的图象对应的函数在下列给出的四个选项中,只可能是
( )
A.y=f(|x|) B.y=|f(x)|
C.y=f(-|x|) D.y=-f(-|x|)[答案] C
[解析] 观察图②可知,当x<0时,y=f(x),当x>0时,y=f(-x),∴图②对应的函数为y=f(-|x|).
二、填空题
5.一等腰三角形的周长为10,底为x,则腰y与x的函数解析式是____________.[解析] 将n=2,3,4,5分别代入函数式,依次可得,
f(2)=f(1)+2×1=1+2=3,
f(3)=f(2)+2×2=3+4=7,
f(4)=f(3)+2×3=7+6=13,
f(5)=f(4)+2×4=13+8=21.
分段函数是一个函数,不是几个函数,只是在定义域的不同范围上取值时对应法则不同,分段函数是普遍存在又比较重要的一种函数.
2.(1)设A、B是两个集合,如果按照某种对应关系f,对于集合A中的 一个元素,在集合B中有 确定的元素和它对应,那么这样的对应(包括A、B以及对应关系f)叫做集合A到B的映射,记作 .分段函数唯一任何f:A→B(2)给定一个集合A到集合B的映射时,a∈A,b∈B如果b和a对应,那么我们把元素b叫做 ,元素a叫做b的 .象原象本节重点:①分段函数概念的理解;②映射定义理解.
本节难点:①函数图象的画法;②分段函数的理解应用;③用映射理解函数的定义.(1)分段函数的定义域是各段自变量取值集合的并集;值域是各段函数值集合的并集;最大(小)值是各段上最大(小)值中的最大(小)者.研究分段函数常借助图象进行.
(2)映射f:A→B包含三个要素:原象集合A,象集合B(或B的子集)以及从集合A到集合B的对应法则f.两个集合A、B可以是数集,也可以是点集或其它集合.对应法则f可用文字表述,也可以用符号表示.映射是一种特殊的对应,它具有:①方向性:映射是有次序的,一般地从A到B的映射与从B到A的映射是不同的;
②任意性:集合A中的任意一个元素都有象,但不要求B中的每一个元素都有原象;
③唯一性:集合A中元素的象是唯一的,即不允许“一对多”但可以“多对一”.[分析] 图象法是表示函数的方法之一,画函数的图象时,以定义域、对应法则为依据,采用列表、描点法作图. 总结评述:函数的图象可以是一些线段,一段曲线,甚至是一些点.表示函数的式子也可以不止一个,这类用几个式子表示的函数叫做分段函数.分段函数是一个函数,而不是几个函数,必须分段画出函数图象,尤其需注意特殊点. [答案] B
[例2] 设f:M→N是集合M到集合N的映射,下列说法中正确的是
( )
A.M中每一个元素在N中必有元素与之对应
B.N中每一个元素在M中必有元素与之对应
C.M中的元素在N中可以有不同元素与之对应
D.N中的元素在M中若有原象,则原象必是惟一的
[分析] 根据映射的定义判断.[解析] 在映射中允许集合N中的某些元素在集合M中没有元素对应,所以B是错误的;又因为映射中允许集合M中不同元素对应集合N中相同的元素,就是说可以“多对一”,因此D也是错误的.M中元素的象是惟一的,故C错,∴选A.[答案] B
[分析] 判断两个集合之间的对应是否为映射,只要按照对应法则f判断,对于集合A中的任何一个元素,在集合B中是否有惟一的元素和它对应.[解析] 在A中,当x=3时,|x-3|=0,于是A中有一个元素在B中没有元素和它对应,故不是映射;在C中,集合A中的负数在B中没有元素和它对应,故也不是映射;(或者x>0时,B中对应元素不唯一);在D中,集合A中元素为0时,其倒数不存在,因而0在B中无对应元素,故同样不是映射;B符合定义,故选B.[例3] 已知集合A=B={(x,y)|x、y∈R},给定映射f:A→B,使得集合A中的元素(x,y)与集合B中的元素(x+y,xy)对应.
(1)求A中元素(-2,3)的象;
(2)求B中元素(2,-3)的原象;
*(3)判断集合A中是否存在元素与B中形如(a,a2)的元素对应;若存在,求之;若不存在,说明理由.
[分析] 由对应法则,可以根据A中元素与B中元素的对应关系建立起关于x、y的方程组.其中第(3)问即是判断相应的方程组是否有解,何时有解. 总结评述:在一个给定的映射f:A→B中,A中每一个元素在B中都有唯一元素与之对应,但B中元素在A中未必有元素对应,即A中元素对应B中元素的集合实际上是集合B的一个子集.在涉及元素的对应问题中,常常需要建立方程组求解.(2)设集合A、B都是正整数集,映射f:A→B把集合A中的元素n映射到集合B中的元素3n+2n,则在映射f下,象89的原象是
( )
A.2 B.3
C.4 D.5
[答案] (1)D (2)C[点评] (2)验证次数要尽可能的少,故先验证B,若n=3时,结果比89小,则排除A、B.若等于89,则知选B,若大于89,则选A.[分析] 这是已知分段函数的函数值求相应自变量的值的问题.一般从两个角度思考:一是先求各段上函数值的取值范围,再结合所给函数值的大小,确定在哪段上求解;二是逐段令其值为已知函数值解出x的值,看是否满足其取值范围的要求做出取舍.[答案] A
[例5] 上因特网的费用由两部分组成:电话费和上网费.以前某“热线”上因特网的费用为电话费0.12元/3分钟,上网费0.12元/分钟.根据信息产业部调整因特网资费的要求,自1999年3月1日起,该地区上因特网的费用调整为电话费0.16元/3分钟,上网费每月不超过60小时,以4元/时计算,超过60小时部分,以8元/时计算.(1)根据调整后的规定,将每月上因特网的费用表示为时间(小时)的函数(每月按30天计算);
(2)某网民在其家庭经济预算中一直有一笔上网60小时的费用开支,因特网资费调整后,若要不超过其家庭经济预算中上网费支出,则该网民现在每月可上网多少小时,从涨价和降价的角度分析该地区调整前后上因特网的费用情况.[解析] 设调整后上网x小时的费用为f(x)元.
(1)当0<x≤60时,f(x)=0.16×20x+4x=7.2x;
当x>60时,f(x)=4×60+0.16×20x+(x-60)×8=11.2x-240.(2)设调整前上网x小时的费用为g(x)元,则g(x)=0.12×20x+0.12×60x=9.6x.
原上网60小时预算费用为9.6×60=576(元),由576=11.2x-240得x≈72.85(时),故该网民现在每月可上网72.85小时.
当0<x≤60时,f(x)<g(x);
当x>60时,由f(x)=g(x),可得x=150.
所以,上网小于150小时时,f(x)<g(x);上网大于150小时时,f(x)>g(x).
如图,在边长为4的正方形ABCD的边上有一点P,沿折线BCDA由点B(起点)向点A(终点)运动,设点P运动的路程为x,△APB的面积为y.
(1)求y关于x的函数关系式y=f(x);
(2)画出y=f(x)的图象;
(3)若△APB的面积不小于2,
求x的取值范围.(2)y=f(x)的图象如图所示.
(3)即f(x)≥2,当0≤x≤4时,2x≥2,∴x≥1,
当8
[错解] ∵B中元素y=3x+1与A中元素x对应,∴A中元素1,2分别对应B中元素4,7.
∵a,k∈N,∴a不存在,∴k不存在.[辨析] 以上解法的错误之处在于误解了映射的定义.由于集合元素的无序性,所以a4=10或a2+3a=10都有可能,因而要分类讨论.一、选择题
1.函数y=|x+1|的图象是 ( )[答案] A
[解析] 当x=-1时y=0,因此否定B、C,又y≥0,否定D,故选A.2.在如图的对应关系中,哪些对应不是集合A到集合B的映射
( )
A.①、②
B.①、④
C.②、⑤
D.①、②、③[答案] D
[解析] 由图知①②中元素a1在B中对应元素不唯一,③中元素a2在B中无象,都不是映射,④⑤是映射,故选D.[答案] B
[解析] 设(x,y)在f作用下对应(3,1),则
∴与(3,1)对应的元素为(1,1),故选B.4.已知图①中的图象对应的函数为y=f(x),则图②的图象对应的函数在下列给出的四个选项中,只可能是
( )
A.y=f(|x|) B.y=|f(x)|
C.y=f(-|x|) D.y=-f(-|x|)[答案] C
[解析] 观察图②可知,当x<0时,y=f(x),当x>0时,y=f(-x),∴图②对应的函数为y=f(-|x|).
二、填空题
5.一等腰三角形的周长为10,底为x,则腰y与x的函数解析式是____________.[解析] 将n=2,3,4,5分别代入函数式,依次可得,
f(2)=f(1)+2×1=1+2=3,
f(3)=f(2)+2×2=3+4=7,
f(4)=f(3)+2×3=7+6=13,
f(5)=f(4)+2×4=13+8=21.
