1-3-1-1函数的单调性

课件53张PPT。1.3　函数的基本性质 1.3.1　单调性与最大(小)值 1.观察函数y＝x2的图象可见，当x≥0时，图象是上升的，称此函数在[0，＋∞)上为增函数，当x≤0时，图象是下降的，称此函数在(－∞，0]上为 函数．
2.一般地，设f(x)的定义域为I，如果对于属于定义域I内某个区间D上的任意两个自变量的值x1、x2，当x1f(x2)如果函数y＝f(x)在某个区间D上是增函数或减函数，那么就说函数y＝f(x)在区间D上具有 ．区间D叫做函数f(x)的单调区间．
(1)如图，已知函数y＝f(x)，y＝g(x)的图象(包括端点)，根据图象说出函数的单调区间，以及在每一个区间上，函数是增函数还是减函数．单调性[解析]　函数f(x)的单调区间有[－2，－1]，[－1，0]，[0,1]，[1,2]．,在区间[－2，－1]，[0,1]上是减函数．
在区间[－1,0]，[1,2]上是增函数．
函数g(x)的单调区间有[－3，－1.5]，[－1.5，1.5]，[1.5,3]．
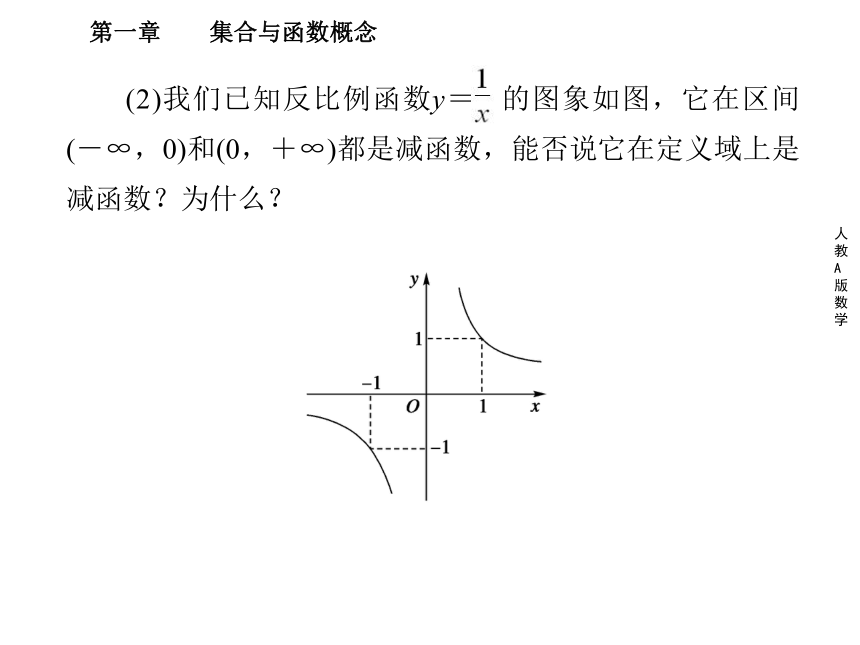
在区间[－3，－1.5]，[1.5,3]上是减函数，在区间[－1.5,1.5]上是增函数．(2)我们已知反比例函数y＝ 的图象如图，它在区间(－∞，0)和(0，＋∞)都是减函数，能否说它在定义域上是减函数？为什么？
[解析]　不能．显然x1＝－1，x2＝1时，满足x1y2不成立．
3．用单调性定义证明：
(1)f(x)＝2x＋1在R上为增函数．
(2)f(x)＝ 在(－∞，0)上为减函数．
并概括用定义证明函数单调性的步骤．
(1)设x1、x2∈R，且x1∴f(x1)本节难点：用定义证明函数的单调性和求函数的单调区间．1．函数的单调性是对某个区间而言的，对于闭区间上的连续函数来说，只要在开区间上单调，它在闭区间上也就单调．因此，在考虑它的单调区间时，包括不包括端点都可以，写单调区间时，一般写成闭区间．但必须注意，对于在某些点上不连续的函数，单调区间不包括不连续点．
2．若f(x)的定义域为D，A?D，B?D，f(x)在A和B上都单调递减，未必有f(x)在A∪B上单调递减．
[例1]　据下列函数图象，指出函数的单调增区间和单调减区间．[解析]　由图象(1)知此函数的增区间为(－∞，2]，[4，＋∞)，减区间为[2,4]．
由图象(2)知，此函数的增区间为(－∞，－1]、[1，＋∞)，减区间为[－1,0)、(0,1].
[例2]　求证函数f(x)＝－x3＋1在(－∞，＋∞)上是减函数．
[分析]　通过对f(x1)－f(x2)符号的判定而得结论．[例3]　已知y＝f(x)与y＝g(x)在区间A上均为增函数，判断下列函数在区间A上的增减性．
(1)y＝－2f(x)　(2)y＝f(x)＋g(x)
[分析]　利用函数单调性的定义判断
[解析]　(1)对任意x1，x2∈A，设x1＜x2，
∵f(x)为增函数，∴f(x1)－f(x2)＜0
∴－2f(x2)－[－2f(x1)]＝2f(x1)－2f(x2)
＝2[f(x1)－f(x2)]＜0
∴－2f(x2)＜－2f(x1)，∴y＝－2f(x)是减函数(2)在区间A内任取两个值x1、x2，设x1＜x2，
∵y＝f(x)，y＝g(x)为增函数
∴f(x2)－f(x1)＞0　g(x2)－g(x1)＞0
∴[f(x2)＋g(x2)]－[f(x1)＋g(x1)]
＝[f(x2)－f(x1)]＋[g(x2)－g(x1)]＞0
∴f(x2)＋g(x2)＞f(x1)＋g(x1)
∴y＝f(x)＋g(x)是增函数[分析]　由定义作差f(x1)－f(x2)，通过a的不同取值对差的符号的影响进行讨论．
已知函数f(x)＝－x2＋(3a－1)x＋1－2a在区间(－∞，4]上是增函数，求实数a的取值范围．
[分析]　二次函数的二次项系数小于0，其图象开口向下，因而只要区间(－∞，4]在对称轴的左侧，即可满足题设要求．[点评]　解决此类问题，首先搞清二次项系数的正负，确定开口方向，然后，考虑单调区间应在对称轴左侧还是右侧．*[例5]　画出函数y＝－x2＋2|x|＋3的图象，并指出函数的单调区间．
[分析]　函数解析式中含有绝对值号，因而需先去掉绝对值号写成分段函数形式，然后，逐段画图．根据图象指出单调区间．[解析]　y＝－x2＋2|x|＋3
函数图象如图所示．
函数在(－∞，－1]，[0,1]上是增函数；
函数在[－1,0]，[1，＋∞)上是减函数．
所以函数的单调增区间是(－∞，－1]和[0,1]，单调减区间是[－1,0]和[1，＋∞)．
画出下列函数的图象，并指出它们的单调区间：
(1)y＝|x|－1；　(2)y＝|x2－1|.
[解析]　(1)如图(1)，函数的单调减区间是(－∞，0]，单调增区间是[0，＋∞)．
函数的图象如图(2)所示．
函数y＝|x2－1|在(－∞，－1]，[0,1]上都是减函数，在[－1,0]，[1，＋∞)上都是增函数．[例6]　若函数f(x)＝x2＋2(a－1)x＋2的单调递减区间是(－∞，4]，则实数a的取值范围是________．
[错解]　函数f(x)图象的对称轴为x＝1－a，由于函数在区间(－∞，4]上单调递减，因此1－a≥4，即a≤－3.
[辨析]　函数f(x)在区间A上单调减和函数f(x)的单调减区间是A不同．
[正解]　因为函数的单调递减区间为(－∞，4]，所以有1－a＝4，即a＝－3.[答案]　B
[解析]　f(x)＝(3a－1)x＋b为增函数，应满足3a－1＞0，即a＞ ，故选B.2．已知函数f(x)＝8＋2x－x2，那么下列结论正确的是
(　　)
A．f(x)在(－∞，1]上是减函数
B．f(x)在(－∞，1]上是增函数
C．f(x)在[－1，＋∞)上是减函数
D．f(x)在[－1，＋∞)上是增函数
[答案]　B
[解析]　由二次函数f(x)＝8＋2x－x2＝－(x－1)2＋9的图象知B对，故选B.3．函数f(x)在区间(－2,3)上是增函数，则y＝f(x＋5)的一个递增区间是
(　　)
A．(3,8) B．(－7，－2)
C．(－2，－3) D．(0,5)
[答案]　B
[解析]　由－2＜x＋5＜3得－7＜x＜－2，选B.
[点评]　y＝f(x＋5)可看作函数y＝f(x)的图象向左平移5个单位得到的．故选B.4．函数f(x)＝|x－a|在(－∞，2]上单调递减，则a的取值范围是
(　　)
A．a≥2 B．a≥1
C．a<2 D．a<1
[答案]　A
[解析]　f(x)＝|x－a|的图象是以(a,0)为折点的折线，由图知a≥2.6．若函数y＝－2x2＋mx－3在[－1，＋∞)上为减函数，则m的取值范围是________．
[答案]　m≤－4