1-3-2-2函数的性质的应用
文档属性
| 名称 | 1-3-2-2函数的性质的应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 860.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-11 00:00:00 | ||
图片预览











文档简介
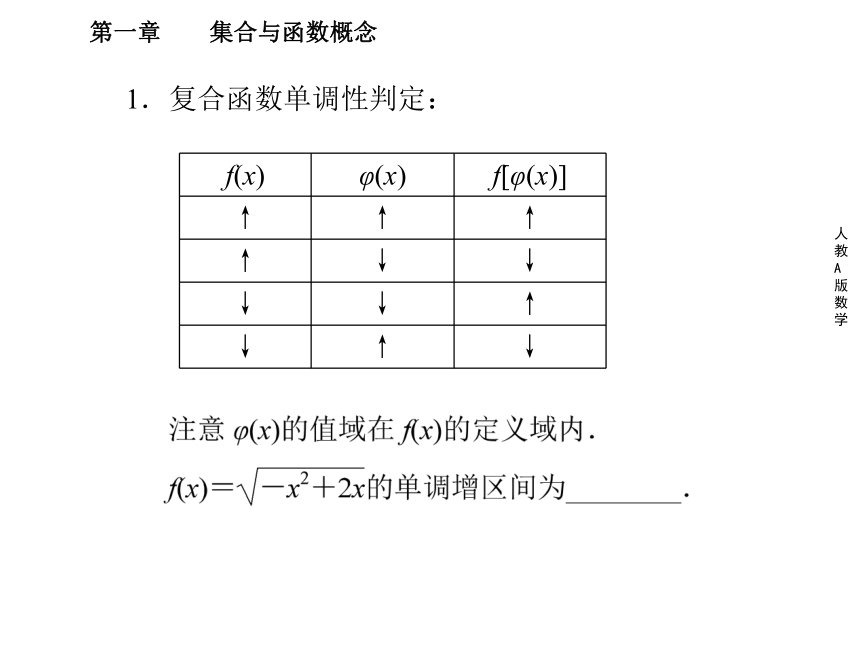
课件50张PPT。1.复合函数单调性判定:
[答案] [0,1]
[解析] 由-x2+2x≥0得0≤x≤2,
当x∈[0,1]时,u=-x2+2x单调增,2.和、差函数的单调性:
两个增函数(或减函数)的和仍为增函数(或减函数)
一个增函数(或减函数)减去一个减函数(或增函数),结果是一个增(或减)函数.[答案] 23.具有奇偶性的两个函数在同一定义域(或定义域的交集上)上有:
奇+奇=奇 奇×奇=偶
奇×偶=奇 偶×偶=偶[答案] -1
本节重点:1.应用单调性比较大小、解不等式及求最值.
2.奇偶函数图象的对称性及奇偶函数的单调性.
本节难点:单调性、奇偶性的综合应用.[分析] 通过分析函数的定义域、值域、奇偶性、单调性等可以了解函数图象的分布情况和对称性,进而可列表描点、画图.[解析] 此函数的定义域为{x∈R|x≠0},故其图象在x=0处断开,即被y轴分为两部分;对任意x≠0,有y>0,故其图象分布在x轴上方;此函数为偶函数,故其图象关于x轴对称,因此只须画出x>0的图象,利用对称性可画出x<0的部分图象;x>0时,f(x)为减函数,x越接近于0,y值越大,其图象越接近于y轴,x越大,y值越小,其图象越靠近x轴.
列出x,y的对应值如表:在直角坐标系中,描点、连成光滑曲线,就得到这个函数的图象,如图.[解析] 定义域[0,+∞)、值域[0,+∞).
因此图象只分布在第一象限内,易知其为增函数,且随着x的增大,增长速度越来越快.列表从略,图象如图.
[例2] 已知f(x)=x5+bx-8,且f(-2)=10,则f(2)等于 ( )
A.-26 B.-18
C.-10 D.10
[解析] 令g(x)=f(x)+8=x5+bx,则g(x)是奇函数,
∴g(-2)+g(2)=0,∴f(-2)+8+f(2)+8=0,
∵f(-2)=10,∴f(2)=-26,∴选A.[分析] 利用函数的性质再得到一个关于f(x)与g(x)的等式,然后把f(x),g(x)看作未知量,利用方程的观点求解f(x),g(x).
[例3] 若函数f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,且f(2)=0,则使得f(x)<0的x的取值范围是
( )
A.(-∞,2) B.(-2,2)
C.(2,+∞) D.(-∞,-2)∪(2,+∞)[解析] 由题意知f(-2)=f(2)=0,
当x∈(-2,0)时,f(x)[点评] 可用数形结合法求解.由题意画出示意图如图所示可知选B.*
已知定义在R+上的函数f(x)是增函数,对任意x1、x2∈R+都有f(x1x2)=f(x1)+f(x2),又f(4)=1,求使不等式f(x+6)+f(x)>2成立的x的取值范围.
[解析] 由条件知,f(16)=f(4×4)=f(4)+f(4)=2,故不等式f(x+6)+f(x)>2,
即f(x+6)+f(x)>f(16)
[例4] 对于每个实数x,设f(x)取y=4x+1,y=x+2,y=-2x+4三个函数中的最小值,用分段函数写出f(x)的解析式,并求f(x)的最大值.
[例5] 已知一个二次函数y=f(x)满足f(0)=3,又知当x=-3或x=-5时,这个函数的值都为0,求这个二次函数.
[解析] 解法1:设f(x)=ax2+bx+c (a≠0),解法2:设f(x)=ax2+bx+c (a≠0),
∵f(0)=3,∴c=3.
令f(x)=0,由韦达定理得
[点评] ①已知二次函数的顶点或对称轴可设配方式f(x)=a(x-h)2+k.
②已知二次函数图象与x轴两交点(x1,0),(x2,0)可设分解式:f(x)=a(x-x1)(x-x2).
③已知二次函数过三点可设一般式f(x)=ax2+bx+c.
(1)已知函数y=f(x)为二次函数,且满足f(0)=-3,f(1)=0,f(-3)=0,则这个二次函数的解析式为______.
(2)已知一个二次函数f(x)的图象的顶点是(6,-12),与x轴的一个交点为(8,0),则其解析式是______.
[答案] (1)f(x)=x2+2x-3 (2)f(x)=3x2-36x+96
[解析] (1)设f(x)=a(x-1)(x+3),
∵f(0)=-3,∴a=1,∴f(x)=x2+2x-3.
(2)设f(x)=a(x-6)2-12,
∵过(8,0)点,∴a=3,∴f(x)=3x2-36x+96.
[例6] 设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时,f(x)的图象如右图,则不等式f(x)<0的解集是______.
[答案] (-2,0)∪(2,5]
[解析] f(x)为奇函数,故由所给图象可知-2<x<0时,f(x)<0又由图知2<x≤5时,f(x)<0,故f(x)<0的解集为(-2,0)∪(2,5].
已知函数y=f(x)是偶函数,y=f(x-2)在[0,2]上是单调减函数,则 ( )
A.f(0)B.f(-1)C.f(-1)D.f(2)[答案] A
[解析] ∵f(x-2)在[0,2]上单调递减,
∴f(x)在[-2,0]上单调递减.
∵y=f(x)是偶函数,∴f(x)在[0,2]上单调递增.
又f(-1)=f(1),故应选A.
[例7] 判断下列函数的奇偶性:[解析] (1)画出函数f(x)的图象,可知f(x)为奇函数.
总结评述:表达式较复杂的函数判断奇偶性,如能化简,应先化简,含绝对值号的常常要先把绝对值号化去;分段函数判断奇偶性常常要利用图象的直观性.利用表达式推证时,要注意自变量的取值范围对应的究竟是哪一段表达式.[例8] 定义在[-1,1]上的偶函数f(x),当x≥0时,f(x) 为增函数,若f(1+m)[错解] ∵x≥0时,f(x)为增函数,且f(1+m)∴0≤1+m<2m,∴m>1.
又f(x)为偶函数,
∴x≤0时,f(x)为减函数,
∵f(1+m)2m,
∴m≤-1.
综上知,m的取值范围是(-∞,-1]或(1,+∞).
[辨析] 本题考查函数奇偶性与单调性的综合应用.欲解不等式f(1+m)则由f(1+m)又x≥0时,f(x)为增函数,
总结评述:本题利用f(x)为偶函数,将f(x1)1.(09·陕西理)定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0](x1≠x2),有(x2-x1)(f(x2)-f(x1))>0,则当n∈N*时,有 ( )
A.f(-n)B.f(n-1)C.f(n+1)D.f(n+1)[答案] C
[解析] 当x2-x1<0时,则f(x2)-f(x1)<0,
∴f(x)在(-∞,0]上单调递增,
∵f(x)为偶函数,
∴f(x)在[0,+∞)上单调递减,
∵n∈N+,∴n+1>n>n-1,
∴f(n+1)∴f(n+1)2.y=(2k+1)x+k-1是减函数,则函数y=kx2+2x-3k+1的增区间为________.
3.f(x)=(ax+1)(x+a)为奇函数,则f(2)=______.
[答案] 2
[解析] 显然x=0时函数f(x)有意义,
∴f(0)=a=0,∴f(x)=x,∴f(2)=2.
4.f(x)为偶函数,当x>0时,f(x)=x|x-1|,则当x<0时,f(x)=________.
[答案] -x|x+1|
[解析] x<0时,-x>0,f(-x)=-x|-x-1|
=-x|x+1|,
∵f(x)为偶函数,∴f(x)=-x|x+1|.5.偶函数f(x)在(0,+∞)上为增函数,若x1<0,x2>0,且|x1|>|x2|,则f(x1)与f(x2)的大小关系是______.
[答案] f(x1)>f(x2)
[解析] ∵x1<0,∴-x1>0,
又|x1|>|x2|,x2>0,∴-x1>x2>0,
∵f(x)在(0,+∞)上为增函数,∴f(-x1)>f(x2),
又∵f(x)为偶函数,∴f(x1)>f(x2).
此类问题利用奇偶函数的对称特征画出示意图一目了然.三、解答题
6.已知函数f(x)=x2+2(1-2a)x+6在(-∞,-1)上为减函数.
(1)求f(2)的取值范围;
(2)比较f(2a-1)与f(0)的大小.
[解析] (1)二次函数图象的对称轴为x=2a-1,
∴原函数在(-∞,2a-1]上为减函数,
∴-1≤2a-1,∴a≥0,
而f(2)=22+2(1-2a)×2+6=-8a+14,
∵a≥0,∴f(2)=14-8a≤14.
(2)∵当x=2a-1时,函数y=f(x)取最小值,
∴f(2a-1)≤f(0).
[答案] [0,1]
[解析] 由-x2+2x≥0得0≤x≤2,
当x∈[0,1]时,u=-x2+2x单调增,2.和、差函数的单调性:
两个增函数(或减函数)的和仍为增函数(或减函数)
一个增函数(或减函数)减去一个减函数(或增函数),结果是一个增(或减)函数.[答案] 23.具有奇偶性的两个函数在同一定义域(或定义域的交集上)上有:
奇+奇=奇 奇×奇=偶
奇×偶=奇 偶×偶=偶[答案] -1
本节重点:1.应用单调性比较大小、解不等式及求最值.
2.奇偶函数图象的对称性及奇偶函数的单调性.
本节难点:单调性、奇偶性的综合应用.[分析] 通过分析函数的定义域、值域、奇偶性、单调性等可以了解函数图象的分布情况和对称性,进而可列表描点、画图.[解析] 此函数的定义域为{x∈R|x≠0},故其图象在x=0处断开,即被y轴分为两部分;对任意x≠0,有y>0,故其图象分布在x轴上方;此函数为偶函数,故其图象关于x轴对称,因此只须画出x>0的图象,利用对称性可画出x<0的部分图象;x>0时,f(x)为减函数,x越接近于0,y值越大,其图象越接近于y轴,x越大,y值越小,其图象越靠近x轴.
列出x,y的对应值如表:在直角坐标系中,描点、连成光滑曲线,就得到这个函数的图象,如图.[解析] 定义域[0,+∞)、值域[0,+∞).
因此图象只分布在第一象限内,易知其为增函数,且随着x的增大,增长速度越来越快.列表从略,图象如图.
[例2] 已知f(x)=x5+bx-8,且f(-2)=10,则f(2)等于 ( )
A.-26 B.-18
C.-10 D.10
[解析] 令g(x)=f(x)+8=x5+bx,则g(x)是奇函数,
∴g(-2)+g(2)=0,∴f(-2)+8+f(2)+8=0,
∵f(-2)=10,∴f(2)=-26,∴选A.[分析] 利用函数的性质再得到一个关于f(x)与g(x)的等式,然后把f(x),g(x)看作未知量,利用方程的观点求解f(x),g(x).
[例3] 若函数f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,且f(2)=0,则使得f(x)<0的x的取值范围是
( )
A.(-∞,2) B.(-2,2)
C.(2,+∞) D.(-∞,-2)∪(2,+∞)[解析] 由题意知f(-2)=f(2)=0,
当x∈(-2,0)时,f(x)
已知定义在R+上的函数f(x)是增函数,对任意x1、x2∈R+都有f(x1x2)=f(x1)+f(x2),又f(4)=1,求使不等式f(x+6)+f(x)>2成立的x的取值范围.
[解析] 由条件知,f(16)=f(4×4)=f(4)+f(4)=2,故不等式f(x+6)+f(x)>2,
即f(x+6)+f(x)>f(16)
[例4] 对于每个实数x,设f(x)取y=4x+1,y=x+2,y=-2x+4三个函数中的最小值,用分段函数写出f(x)的解析式,并求f(x)的最大值.
[例5] 已知一个二次函数y=f(x)满足f(0)=3,又知当x=-3或x=-5时,这个函数的值都为0,求这个二次函数.
[解析] 解法1:设f(x)=ax2+bx+c (a≠0),解法2:设f(x)=ax2+bx+c (a≠0),
∵f(0)=3,∴c=3.
令f(x)=0,由韦达定理得
[点评] ①已知二次函数的顶点或对称轴可设配方式f(x)=a(x-h)2+k.
②已知二次函数图象与x轴两交点(x1,0),(x2,0)可设分解式:f(x)=a(x-x1)(x-x2).
③已知二次函数过三点可设一般式f(x)=ax2+bx+c.
(1)已知函数y=f(x)为二次函数,且满足f(0)=-3,f(1)=0,f(-3)=0,则这个二次函数的解析式为______.
(2)已知一个二次函数f(x)的图象的顶点是(6,-12),与x轴的一个交点为(8,0),则其解析式是______.
[答案] (1)f(x)=x2+2x-3 (2)f(x)=3x2-36x+96
[解析] (1)设f(x)=a(x-1)(x+3),
∵f(0)=-3,∴a=1,∴f(x)=x2+2x-3.
(2)设f(x)=a(x-6)2-12,
∵过(8,0)点,∴a=3,∴f(x)=3x2-36x+96.
[例6] 设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时,f(x)的图象如右图,则不等式f(x)<0的解集是______.
[答案] (-2,0)∪(2,5]
[解析] f(x)为奇函数,故由所给图象可知-2<x<0时,f(x)<0又由图知2<x≤5时,f(x)<0,故f(x)<0的解集为(-2,0)∪(2,5].
已知函数y=f(x)是偶函数,y=f(x-2)在[0,2]上是单调减函数,则 ( )
A.f(0)
[解析] ∵f(x-2)在[0,2]上单调递减,
∴f(x)在[-2,0]上单调递减.
∵y=f(x)是偶函数,∴f(x)在[0,2]上单调递增.
又f(-1)=f(1),故应选A.
[例7] 判断下列函数的奇偶性:[解析] (1)画出函数f(x)的图象,可知f(x)为奇函数.
总结评述:表达式较复杂的函数判断奇偶性,如能化简,应先化简,含绝对值号的常常要先把绝对值号化去;分段函数判断奇偶性常常要利用图象的直观性.利用表达式推证时,要注意自变量的取值范围对应的究竟是哪一段表达式.[例8] 定义在[-1,1]上的偶函数f(x),当x≥0时,f(x) 为增函数,若f(1+m)
又f(x)为偶函数,
∴x≤0时,f(x)为减函数,
∵f(1+m)
∴m≤-1.
综上知,m的取值范围是(-∞,-1]或(1,+∞).
[辨析] 本题考查函数奇偶性与单调性的综合应用.欲解不等式f(1+m)
总结评述:本题利用f(x)为偶函数,将f(x1)
A.f(-n)
[解析] 当x2-x1<0时,则f(x2)-f(x1)<0,
∴f(x)在(-∞,0]上单调递增,
∵f(x)为偶函数,
∴f(x)在[0,+∞)上单调递减,
∵n∈N+,∴n+1>n>n-1,
∴f(n+1)
3.f(x)=(ax+1)(x+a)为奇函数,则f(2)=______.
[答案] 2
[解析] 显然x=0时函数f(x)有意义,
∴f(0)=a=0,∴f(x)=x,∴f(2)=2.
4.f(x)为偶函数,当x>0时,f(x)=x|x-1|,则当x<0时,f(x)=________.
[答案] -x|x+1|
[解析] x<0时,-x>0,f(-x)=-x|-x-1|
=-x|x+1|,
∵f(x)为偶函数,∴f(x)=-x|x+1|.5.偶函数f(x)在(0,+∞)上为增函数,若x1<0,x2>0,且|x1|>|x2|,则f(x1)与f(x2)的大小关系是______.
[答案] f(x1)>f(x2)
[解析] ∵x1<0,∴-x1>0,
又|x1|>|x2|,x2>0,∴-x1>x2>0,
∵f(x)在(0,+∞)上为增函数,∴f(-x1)>f(x2),
又∵f(x)为偶函数,∴f(x1)>f(x2).
此类问题利用奇偶函数的对称特征画出示意图一目了然.三、解答题
6.已知函数f(x)=x2+2(1-2a)x+6在(-∞,-1)上为减函数.
(1)求f(2)的取值范围;
(2)比较f(2a-1)与f(0)的大小.
[解析] (1)二次函数图象的对称轴为x=2a-1,
∴原函数在(-∞,2a-1]上为减函数,
∴-1≤2a-1,∴a≥0,
而f(2)=22+2(1-2a)×2+6=-8a+14,
∵a≥0,∴f(2)=14-8a≤14.
(2)∵当x=2a-1时,函数y=f(x)取最小值,
∴f(2a-1)≤f(0).
